Технологическая карта урока геометрии в 8 классе
подготовила
учитель математики Федоренко Т.Н.
МБОУ специализированная школа №1
| Тема: «Решение задач по теме «Площадь»». Тип урока: закрепления и укрупнения знаний.
| ||||||||||||||||||||||||||||||||
| Этапы урока | Задачи этапа | Деятельность учителя | Деятельность учащихся | УУД | ||||||||||||||||||||||||||||||||||||||||||||
| 1. Организационный момент | Создать благоприятный психологический настрой на работу | Здравствуйте ребята! Меня зовут Федоренко Т.Н., я учитель математики специализированной школы №1, но сегодня я провожу урок у вас. | Включаются в деловой ритм урока. | Личностные: самоопределение.
| ||||||||||||||||||||||||||||||||||||||||||||
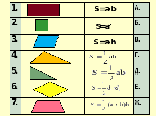
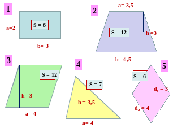
| 2. Актуализация и фиксирование индивидуального затруднения в пробном учебном действии. | Актуализация опорных знаний и способов действий. | Давайте вспомним, что вы уже знаете: у вас на партах лежит набор формул, и мы не произнеся ни слово, установим соответствие между данными формулами и фигурами, которые вы увидите сейчас на экране.
(На экране появляются фигуры и после ответов формулы)
Молодцы! А теперь обратите внимание на карточки, которые находятся у вас на столе. Возьмите конверты, в них формулы, прикрепите их в соответствии с данными фигурами.
Проверьте, правильно ли вы выполнили (слайд)
В течении урока вы будите проводить самооценку своей работы на бланках, обратите на них внимание. Максимальная оценка за это задание - 7 баллов | Из предложенных формул выбирают те, которые соответствуют данной фигуре, поднимают вверх необходимую формулу.
Самопроверка с таблицей на доске
Заполняют листы самооценки | Коммуникативные: планирование учебного сотрудничества с учителем и сверстником.
Личностные: самоопределение.
| ||||||||||||||||||||||||||||||||||||||||||||
| 3. Целеполагание и построение проекта коррекции выявленных затруднений. | Обеспечение мотивации учения детьми, принятие ими целей урока. -Ученики самостоятельно выходят на проблему и решают ее; -Самостоятельно определяют тему, цели урока; -подбирают способы решения задач и формулы;
| А вы знаете, что много лет назад жил древнегреческий философ Платон, который основал собственную школу академию. Над воротами Академии Платона было написано: "Не знающий геометрии да не войдет сюда". (Вывести на слайд и прикрепить на доску) Как вы считаете, можем ли мы назвать себя знатоками геометрии? Да, я тоже считаю, что мы можем войти в эту школу. Как вы думаете, что мы будем делать в школе? А по какой теме мы будем решать задачи? Правильно мы будем сегодня заниматься решением задач по теме «Площади»
Откройте тетради, запишите сегодняшнее число, тему урока
Давайте решим несколько устных задач Как вы считаете, для чего нам необходимо научится решать задачи? |
Ответы учащихся
Решать задачи Делают вывод: Цель урока: -Нахождение площадей фигур Задачи: -Закрепить знания и умения в вычислении площадей многоугольников; -Применять изученные формулы для нахождения площадей фигур к решению задач.
Устные ответы с мест с пояснениями | Регулятивные: целеполагание. Коммуникативные: постановка вопросов. Познавательные: самостоятельное выделение-формулирование познавательной цели; логические - формулирование проблемы. | ||||||||||||||||||||||||||||||||||||||||||||
| 4. Операционно-исполнительский этап | Работа по нахождению площадей фигур (раздать карточки). Давайте обсудим пути решения этих задач.
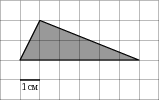
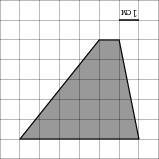
| А еще вам предстоит в конце 9-го класса сдавать ГИА, где встречаются задачи на клетчатой бумаге. Например, такая (на экране задача о прямоугольнике).
Кто из вас может объяснить нам как ее решать? Давайте решим еще несколько заданий из открытого банка ФИПИ.
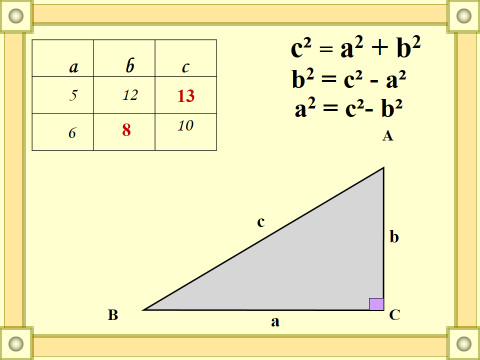
Такие задачи были внесены в главный труд древнегреческого математика Эвклида, учебник «Начала», люди в течении двух тысячелетий изучали геометрию по этому учебнику. Значит мы могли бы с вами учиться и в школе Евклид Оцените свою работу на бланке самооценки Еще один известный древнегреческий философ и геометр Пифагор. А чем знаменит Пифагор? Сформулируйте и запишите теорему Пифагора на доске и в тетради. Как найти по теореме гипотенузу, как найти неизвестный катет?
Решите задачи на применение теоремы Пифагора. А еще Пифагор был чемпионом античных Олимпийских игр. Давайте и мы с вами немного разомнемся Пифагор организовал свой Пифагорейский орден и Школу философов, и математиков. Туда принимали с большими церемониями и после долгих испытаний. В школе была очень серьезная дисциплина, существовали строгие правила –заповеди. Давайте узнаем какие? Решите верно задачи и составьте текст заповедей. Учитель (ученики по рядам) раздает карточки с заданиями. Учитель инструктирует.
Карточка I.
Ответ: Не гоняйся за счастьем, оно всегда находится в тебе самом. Карточка II.
Ответ: Числа управляют миром. Карточки для III
Ответ: Либо молчи, либо говори то, что ценнее молчания. После выполнения, поднимите по рядам, какие же заповеди были в Пифагорейской школе? (Прикрепить на доску) Заполните бланк самооценки, максимальный балл -3 Часто встречаются задачи, в которых необходимо доказать, что треугольник прямоугольный. Знание какой теоремы нам пригодится в этом случае? Давайте вспомним обратную теорему Пифагора Назовите тройки чисел подтверждающие это утверждение. Составьте на бланках три Пифагоровы тройки После ответов учеников вывести слайд Пифагор был не только великим геометром, но и философом древности, он считал, что «Числа правят миром». Вы согласны с этим высказыванием? Не числа правят миром, а мы с их помощью решаем множество практических задач, таких например, как эта - Вычислите стоимость ламината, который нужно уложить в комнате длиной 5,5 м и шириной 4.5 м, если одна доска 20 см×130 см. Стоимость одной дощечки 156 руб.
|
Ученики дают свои варианты решения (учитель корректирует правильность решения)
Один у доски, остальные решают самостоятельно задачи
Теоремой Пифагора
Устные ответы с мест
Выполняют физкультминутку
Работа в парах, решают задачи и собирают «Заповеди Пифагора»
Демонстрируют полученные результаты Ответы с мест
Работают с бланком на местах
Работают с бланком на местах | Коммуникативные: постановка вопросов, инициативное сотрудничество. Познавательные: самостоятельное выделение-формулирование познавательной цели; логические- формулирование проблемы, решение проблемы, построение логической цепи рассуждений; доказательство. Регулятивные: планирование, прогнозирование. | ||||||||||||||||||||||||||||||||||||||||||||
| 5. Подведение итогов урока | Дать качественную оценку работы класса и отдельных обучаемых Выявление качества и уровня усвоения знаний и способов действий | Мы гуляли по знаменитой школе Пифагора, Академии Платона, говорили об учебнике Эвклида. Посмотрите на свои карточки. Чем же занимались сегодня на уроке? Правильно, мы вспомнили как находить площади многоугольников, Теорему Пифагора и обратную к ней, решали задачи из открытого банка ФИПИ. Покажите результаты вашего труда. Вы хотели бы, чтобы эти карточки были у вас на уроке, пригодятся ли они вам дальнейшей учебе, дома? Вернемся к бланку самооценки, подведите итог и выставьте себе оценку согласно критериям | -Расширили свои знания по вычислению площадей многоугольников -Учились применять формулы... -Научились решать некоторые задачи ГИА. | Регулятивные: контроль, оценка, коррекция. Познавательные: умение структурировать знания, выбор наиболее эффективных способов решения задач
| ||||||||||||||||||||||||||||||||||||||||||||
| 6. Рефлексия | Инициировать рефлексию детей по поводу психоэмоционального состояния, мотивации их собственной деятельности и взаимодействия с учителем и другими детьми в классе. | Оцените: свою работу на уроке с помощью фраз: - Сегодня на уроке я научился- - Я пока еще не умею …. - Я стал лучше…. Оцените свою работу смайликом: Радостным- если вы считаете, что поняли тему урока. Нейтральным - если вы считаете, что не достаточно усвоили материал. Грустным - если вы считаете, что не поняли тему урока. | Ученики заполняют листы самоконтроля, выставляют баллы; наклеивают на свой лист квадратик того цвета, как они оценивают свое настроение в конце занятия | Коммуникативные: умение с достаточной полнотой и точностью выражать свои мысли; Познавательные: рефлексия. | ||||||||||||||||||||||||||||||||||||||||||||
| 7. Домашнее задание |
| Повторить § 49-57 Рассчитать стоимость ремонта одной из комнат вашего дома. Все необходимые данные найдите сами. - На отметку «3»: покраска пола и потолка - На отметку «4»: укладка ламината и оклеивание потолка плиткой - На отметку «5»: укладка ламината, оклеивание потолка плиткой и стен обоями
|
|
|
Лист самоконтроля _______________( Фамилия, Имя) Лист самоконтроля _______________( Фамилия, Имя)
| Форма работы | Возможное количество баллов | Количество баллов | Форма работы | Возможное количество баллов | Количество баллов |
| Знание формул | 7 баллов | | Знание формул | 7 баллов | |
| Решение задач на вычисление площадей | 5 баллов | | Решение задач на вычисление площадей | 5баллов | |
| Задачи на клетчатой бумаге | 2 балла | | Задачи на клетчатой бумаге | 2 балла | |
| Заповеди Пифагора | 3 балла | | Заповеди Пифагора | 3балла | |
| Активность на уроке (устные ответы, у доски) | 3 балла | | Активность на уроке (устные ответы, у доски) | 3балла | |
| Итого | 20 баллов | | Итого | 20 баллов | |
Критерии оценивания
На отметку «3»: от 8 до12 баллов
На отметку «4»: от 13 до16 баллов
На отметку «5»: от 17 до 20 баллов
Карточка I.
| №1. Катеты прямоугольного треугольника равны 3 и 4 см. Вычислите его гипотенузу. | №2. Диагональ прямоугольника ABCD - 10 см. Сторона АВ = 8 см. Вычислите сторону ВС. |
| Ответы к задаче №1 | Ответы к задаче №2 |
| 5 – не гоняйся за счастьем | 4 – оно присутствует около тебя |
| 6 – не бегай за счастьем | 6 – оно всегда находится в тебе самом |
Карточка II.
| №1. Вычислите катет прямоугольного треугольника, если другой катет равен 8, а гипотенуза 10 см. | №2. Стороны прямоугольника равны 12 см и 5 см. Вычислите длину диагонали. |
| Ответы к задаче №1 | Ответы к задаче №2 |
| 4 – формулы | 13 – управляют миром |
| 6 – числа | 14 – правят всем |
Карточки для III
| №1.Вычислите катет прямоугольного треугольника, если две другие его стороны равны 15 и 17 см. | №2. Найти боковую сторону равнобедренного треугольника, если основание равно 8см, а высота, опущенная на основание - 3см. |
| Ответы к задаче №1 | Ответы к задаче №2 |
| 8 – либо молчи | 5 – либо говори то, что ценнее молчания |
| 64 – хочешь-молчи | 6 – или говори о том, что интересно всем |
| не гоняйся за счастьем |
оно присутствует около тебя |
| не бегай за счастьем | оно всегда находится в тебе самом |
| не гоняйся за счастьем |
оно присутствует около тебя |
| не бегай за счастьем | оно всегда находится в тебе самом |
| не гоняйся за счастьем |
оно присутствует около тебя |
| не бегай за счастьем | оно всегда находится в тебе самом |
| не гоняйся за счастьем |
оно присутствует около тебя |
| не бегай за счастьем | оно всегда находится в тебе самом |
| не гоняйся за счастьем |
оно присутствует около тебя |
| не бегай за счастьем | оно всегда находится в тебе самом |
| не гоняйся за счастьем |
оно присутствует около тебя |
| не бегай за счастьем | оно всегда находится в тебе самом |
| формулы | управляют миром |
| числа | правят всем |
| формулы | управляют миром |
| числа | правят всем |
| формулы | управляют миром |
| числа | правят всем |
| формулы | управляют миром |
| числа | правят всем |
| формулы | управляют миром |
| числа | правят всем |
| формулы | управляют миром |
| числа | правят всем |
| формулы | управляют миром |
| числа | правят всем |
| либо молчи | либо говори то, что ценнее молчания |
| хочешь-молчи | или говори о том, что интересно всем |
| либо молчи | либо говори то, что ценнее молчания |
| хочешь-молчи | или говори о том, что интересно всем |
| либо молчи | либо говори то, что ценнее молчания |
| хочешь-молчи | или говори о том, что интересно всем |
| либо молчи | либо говори то, что ценнее молчания |
| хочешь-молчи | или говори о том, что интересно всем |
| либо молчи | либо говори то, что ценнее молчания |
| хочешь-молчи | или говори о том, что интересно всем |
Заповеди Пифагора
Не гоняйся за счастьем, оно всегда находится в тебе самом.
Числа управляют миром.
Либо молчи, либо говори то,
что ценнее молчания.
|
|
|
|
|
|
|
S= a2 |
|
|
|
|
|
|
|
|
S= a2 |
|
|
|
|
|
|
|
|
| S= a2 |
|
|
S = ab |
|
|
|
|
S = ab |
| S= a2 |
|
|
S = ab |
|
|
|
|
|
| S= a2 |
|
|
S = ab |
|
|
|
|
|
| S= a2 |
|
|
S = ab |
|
|
|
|
|
| S= a2 |
|
|
S = ab |
|
|
|
|
|
| S= a2 |
|
|
S = ab |
|
|
|
|
|
| S= a2 |
|
|
S = ab |
|
|
|
|
|
| S= a2 |
|
|
S = ab |
|
|
|
| S= a2 |
| S= a2 |
|
|
S = ab |
| S= a2
|
|
|
|
|
|
|
|
|
| S = ab |

 Получите свидетельство
Получите свидетельство Вход
Вход




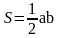
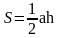
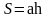
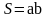









 Геометрия 8 класс "Решение задач по теме Площадь" (222.49 KB)
Геометрия 8 класс "Решение задач по теме Площадь" (222.49 KB)
 0
0 469
469 25
25 Нравится
0
Нравится
0


