Функции и их свойства. Графики

Кусочно-непрерывные функции

1. По­строй­те гра­фик функ­ции 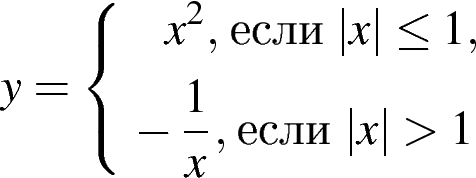  и опре­де­ли­те, при каких зна­че­ни­ях па­ра­мет­ра пря­мая имеет с гра­фи­ком ровно одну общую точку.

2. По­строй­те гра­фик функ­ции 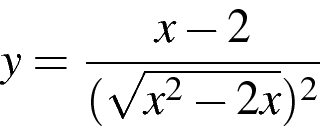 и най­ди­те все зна­че­ние , при ко­то­рых пря­мая  имеет с гра­фи­ком дан­ной функ­ции ровно одну общую точку.

3. По­строй­те гра­фик функ­ции 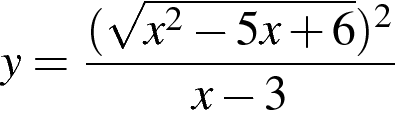 и най­ди­те все зна­че­ния , при ко­то­рых пря­мая  не имеет с гра­фи­ком дан­ной функ­ции общих точек.

4. По­строй­те гра­фик функ­ции    и опре­де­ли­те, при каких зна­че­ни­ях    пря­мая    имеет с гра­фи­ком три общие точки.

5. По­строй­те гра­фик функ­ции и най­ди­те зна­че­ния , при ко­то­рых пря­мая имеет с ним ровно две общие точки.

6. По­строй­те гра­фик функ­ции

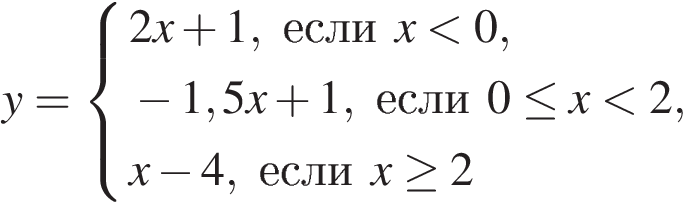
и опре­де­ли­те, при каких зна­че­ни­ях пря­мая имеет с гра­фи­ком ровно две общие точки.

7. По­строй­те гра­фик функ­ции и опре­де­ли­те, при каких зна­че­ни­ях пря­мая не будет иметь с по­стро­ен­ным гра­фи­ком ни одной общей точки.

8. По­строй­те гра­фик функ­ции 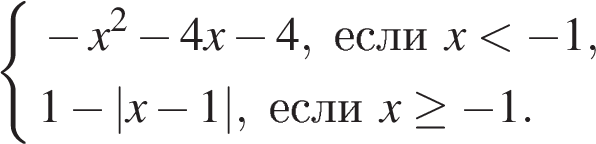и опре­де­ли­те, при каких зна­че­ни­ях па­ра­мет­ра a он имеет ровно две общие точки с пря­мой y = a.

9. По­строй­те гра­фик функ­ции

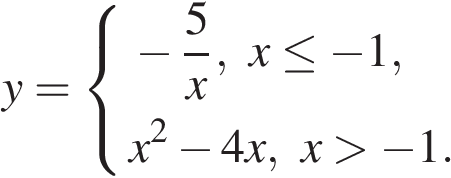
и опре­де­ли­те, при каких зна­че­ни­ях пря­мая будет пе­ре­се­кать по­стро­ен­ный гра­фик в трёх точ­ках.

10. По­строй­те гра­фик функ­ции и опре­де­ли­те, при каких зна­че­ни­ях пря­мая имеет с гра­фи­ком ровно три общие точки.

11. По­строй­те гра­фик функ­ции

и опре­де­ли­те, при каких зна­че­ни­ях пря­мая будет иметь с гра­фи­ком един­ствен­ную общую точку.

12. По­строй­те гра­фик функ­ции

и опре­де­ли­те, при каких зна­че­ни­ях пря­мая будет пе­ре­се­кать по­стро­ен­ный гра­фик в трёх точ­ках.

13. По­строй­те гра­фик функ­ции и най­ди­те все зна­че­ния при ко­то­рых пря­мая имеет с гра­фи­ком дан­ной функ­ции ровно одну общую точку.

14. По­строй­те гра­фик функ­ции и най­ди­те все зна­че­ния при ко­то­рых он имеет ровно три общие точки с пря­мой

15. По­строй­те гра­фик функ­ции

и опре­де­ли­те, при каких зна­че­ни­ях m пря­мая y = m имеет с гра­фи­ком ровно две общие точки.

16. По­строй­те гра­фик функ­ции и опре­де­ли­те, при каких зна­че­ни­ях пря­мая имеет с гра­фи­ком ровно три общие точки.

17. По­строй­те гра­фик функ­ции и опре­де­ли­те, при каких зна­че­ни­ях пря­мая имеет с гра­фи­ком ровно две общие точки.

18. По­строй­те гра­фик функ­ции и опре­де­ли­те, при каких зна­че­ни­ях пря­мая имеет с гра­фи­ком ровно три общие точки.

19. По­строй­те гра­фик функ­ции и опре­де­ли­те, при каких зна­че­ни­ях пря­мая имеет с гра­фи­ком ровно одну общую точку.

20. По­строй­те гра­фик функ­ции и опре­де­ли­те, при каких зна­че­ни­ях пря­мая не имеет с гра­фи­ком ни одной общей точки.

21. По­строй­те гра­фик функ­ции Какое наи­боль­шее число общих точек гра­фик дан­ной функ­ции может иметь с пря­мой, па­рал­лель­ной оси абс­цисс?

22. По­строй­те гра­фик функ­ции

и опре­де­ли­те, при каких зна­че­ни­ях пря­мая имеет с гра­фи­ком одну или две общие точки.

23. По­строй­те гра­фик функ­ции

и опре­де­ли­те, при каких зна­че­ни­ях m пря­мая y = m имеет с гра­фи­ком ровно две общие точки.

24. По­строй­те гра­фик функ­ции

и опре­де­ли­те, при каких зна­че­ни­ях m пря­мая y = m имеет с гра­фи­ком ровно две общие точки.

25. По­строй­те гра­фик функ­ции и опре­де­ли­те, при каких зна­че­ни­ях m пря­мая y = m имеет с гра­фи­ком ровно одну общую точку.

26. По­строй­те гра­фик функ­ции и опре­де­ли­те, при каких зна­че­ни­ях m пря­мая y = m не имеет с гра­фи­ком ни одной общей точки.

27. По­строй­те гра­фик функ­ции

и опре­де­ли­те, при каких зна­че­ни­ях пря­мая имеет с гра­фи­ком ровно две общие точки.

28. По­строй­те гра­фик функ­ции . Какое наи­боль­шее число общих точек гра­фик дан­ной функ­ции может иметь с пря­мой, па­рал­лель­ной оси абс­цисс?

29. По­строй­те гра­фик функ­ции

и опре­де­ли­те, при каких зна­че­ни­ях пря­мая имеет с гра­фи­ком ровно две общие точки.

30. По­строй­те гра­фик функ­ции и най­ди­те зна­че­ния , при ко­то­рых пря­мая имеет с ним ровно три общие точки.

31. По­строй­те гра­фик функ­ции . Опре­де­ли­те, при каких зна­че­ни­ях пря­мая имеет с гра­фи­ком ровно одну общую точку.

32. Най­ди­те  и по­строй­те гра­фик функ­ции, если из­вест­но, что пря­мая  имеет с гра­фи­ком ровно одну общую точку.