МАТЕРИАЛЫ ДЛЯ УСТНОЙ РАБОТЫ НА УРОКАХ АЛГЕБРЫ В 7 КЛАССЕ
- Устные тесты,
- устные упражнения;
- математические диктанты,
- развивающие таблицы.
Учитель Козина Н.А.
ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ
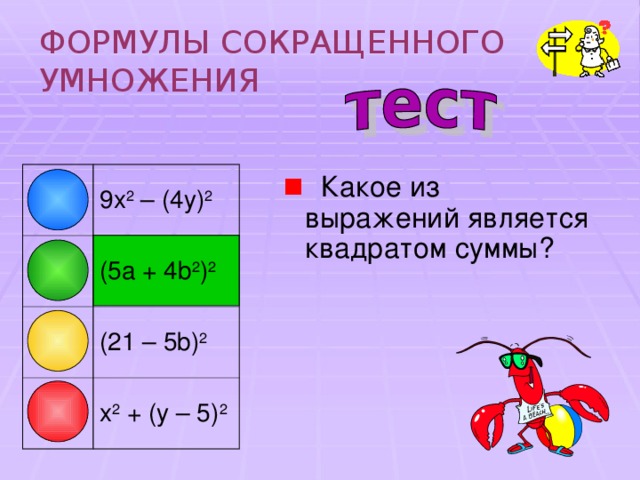
- Какое из выражений является квадратом суммы?
9x 2 – (4y) 2
(5a + 4b 2 ) 2
(21 – 5b) 2
x 2 + (y – 5) 2
ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ
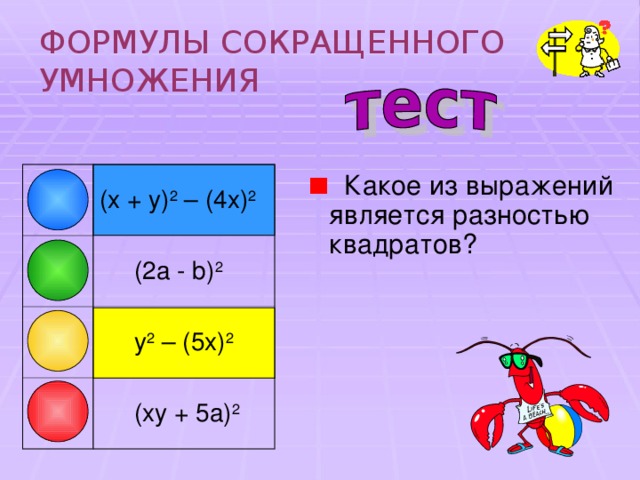
- Какое из выражений является разностью квадратов?
( x + y) 2 – (4x) 2
(2a - b) 2
y 2 – (5x) 2
(xy + 5a) 2
ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ
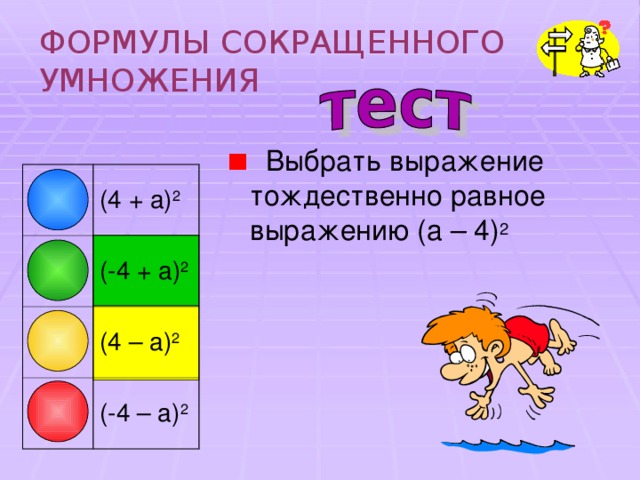
- Выбрать выражение тождественно равное выражению (a – 4) 2
(4 + a) 2
(-4 + a) 2
(4 – a) 2
(-4 – a) 2
ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ
I вариант
II вариант
(5 + y) 2
(4 + a) 2
(1 - 3a) 2
(2c - 1) 2
(2c - 3b) 2
(3b + 2a) 2
(y 2 + 5) 2
(x 4 - 3) 2
(-x - 3x 2 ) 2
(-2m 3 – m) 2
ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ
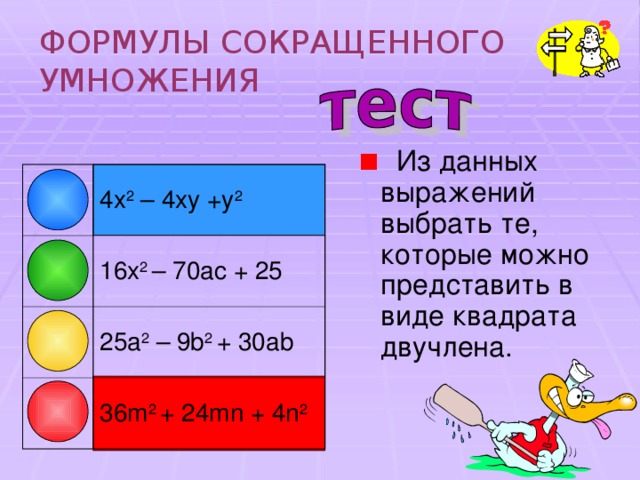
- Из данных выражений выбрать те, которые можно представить в виде квадрата двучлена.
4 x 2 – 4xy +y 2
16x 2 – 70ac + 25
25a 2 – 9b 2 + 30ab
36m 2 + 24mn + 4n 2
ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ
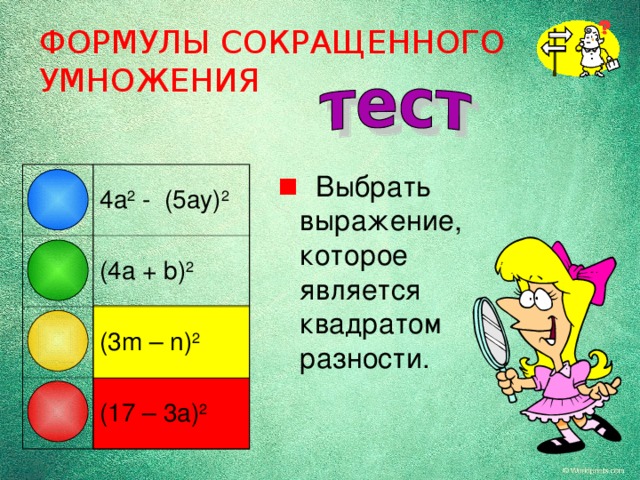
- Выбрать выражение, которое является квадратом разности.
4a 2 - (5ay) 2
(4a + b) 2
(3m – n) 2
(17 – 3a) 2
ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ
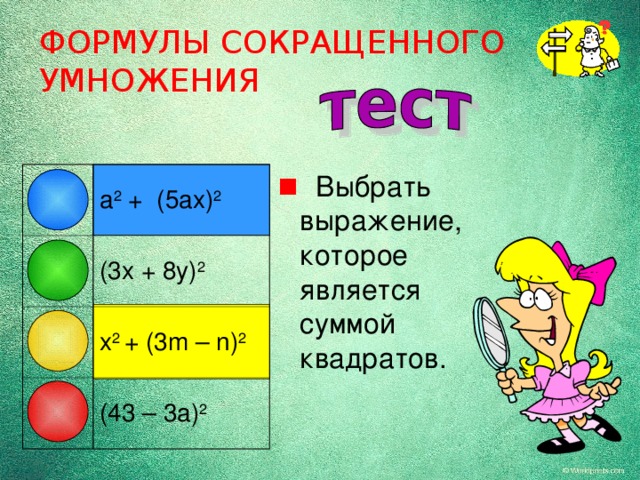
- Выбрать выражение, которое является c уммой квадратов.
a 2 + (5ax) 2
(3x + 8y) 2
x 2 + (3m – n) 2
(43 – 3a) 2
ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ
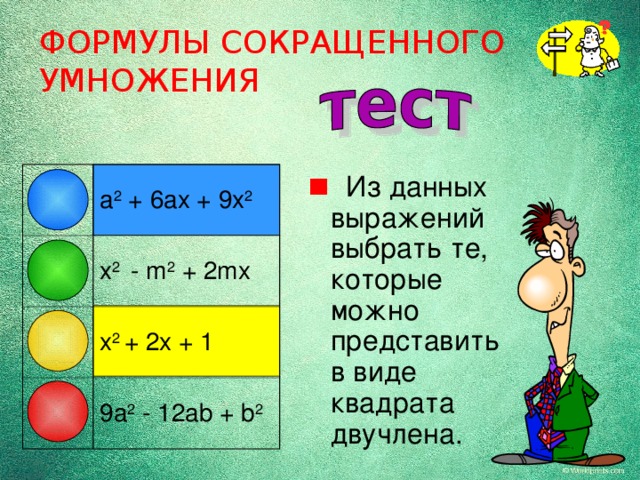
- Из данных выражений выбрать те, которые можно представить в виде квадрата двучлена.
a 2 + 6 ax + 9x 2
x 2 - m 2 + 2mx
x 2 + 2x + 1
9a 2 - 12ab + b 2
ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ
- Из данных выражений выбрать те, которые тождественно равны выражению (x – 5) 2 .
(5 + x) 2
(-x + 5) 2
(-x – 5) 2
(5 – x) 2
ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ
ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ
- Прочитайте выражения:
- m 2 –n 2 ;
- (2+c) 2 ;
- x 2 + y 2 ;
- (a-b) 2 ;
- 2xy.
ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ
- Раскройте скобки:
- ( a-7) 2
ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ
- Из данных выражений выбрать те, которые являются разностью квадратов двух выражений.
4 x 2 - 9
-x 2 - y 2
0,64x 8 – b 2
0,4 – x 2
ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ
- Из данных выражений выбрать те, которые являются разностью квадратов двух выражений.
- 4 m 2 – 0,01
-16x 2 + 4y 2
0,9x 4 – y 2
0,25 – 36x 8
ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ
- Из данных выражений выбрать те, которые можно представить в виде разности квадратов.
( x – 5)(x + 4)
(y + 5)(y – (-5))
(-3 + a)(3 + a)
(x – y)(y +x)
ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ
- Из данных выражений выбрать те, которые можно представить в виде разности квадратов.
( -5 + x)(5 + x)
(a + 4)(a – 3)
(m - n)(n + m)
(x – (-y))(y +x)
ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ
- В древности были известны только 5 планет, видимые невооруженным глазом. Замените заданные выражения многочленами стандартного вида. Используя найденные ответы и данные таблицы, узнайте, какие это были планеты.
ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ
Ответы
Планеты
x 2 + 2ax + a 2
Венера
a 2 – 4ax + 4x 2
Марс
x 2 + 4ax + 4a 2
Меркурий
4x 2 – 9a 2
Нептун
a 2 – 2ax + 4x 2
4x 2 – 12ax + 9a 2
Плутон
x 2 + 4a 2
Сатурн
x 2 – 2a 2 x + a 4
Уран
Юпитер
- (x + a) 2 =
- (a – 2x) 2 =
- (x + 2a) 2 =
- (2x – 3a) 2 =
- (a 2 – x) 2 =
- Венера
- Марс
- Меркурий
- Сатурн
- Юпитер
ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ
- Остальные 3 планеты - Нептун, Плутон и Уран – были открыты за последние 200 лет.
ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ
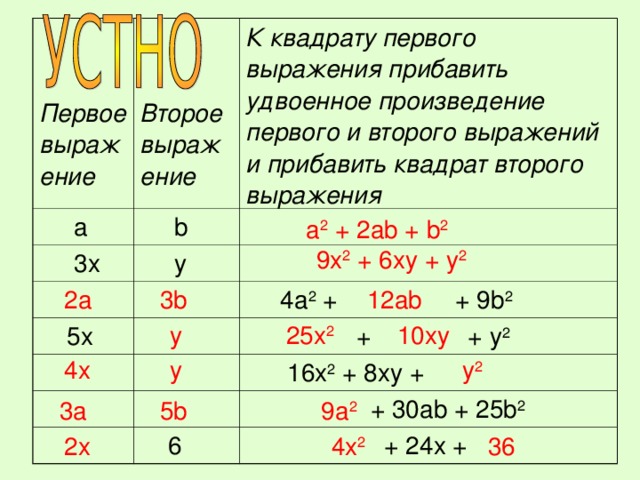
- Заполните пропуски, если конструирование выражений ведется по правилу, записанному в таблице:
Первое выражение
Второе выражение
a
b
3x
К квадрату первого выражения прибавить удвоенное произведение первого и второго выражений и прибавить квадрат второго выражения
y
5x
4a 2 + + 9b 2
+ + y 2
16x 2 + 8xy +
6
+ 30ab + 25b 2
+ 24x +
a 2 + 2ab + b 2
9x 2 + 6xy + y 2
3b
12ab
2a
y
25x 2
10xy
4x
y
y 2
5b
3a
9a 2
36
2x
4x 2
ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ
- (x □ y) 2 = x 2 -2xy + ____
- (__ - __) 2 = 9x 2 □ ____ + 25y 2
- (__ + __) 2 = 36x 2 □ 12xy + ____
- (__ □ __) 2 = ____ - 28xy □ 49x 2
- (x - ___) 2 = ____□ 20x □ ____
- (___ - 3) 2 = ____ □ 48x □ ____
- y 2
3x 5y – 30xy
6x y + y 2
2y - 7x 4y 2 +
10 x 2 - + 100
8x 64x 2 - + 9
ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ
- Долгое время одну из известных в древности планет в периоды утренней и вечерней видимости греки считали двумя разными светилами.
- Упростите заданные алгебраические выражения. Зачеркните в таблице названия планет, связанные с найденными ответами. Оставшееся название позволит вам узнать, с какой планетой это заблуждение было связано.
4a + 7
Юпитер
-5a - 1
Сатурн
3a 2 + 4a
Венера
1 – 4a
3a 2 – 4a
Марс
Меркурий
ФОРМУЛЫ СОКРАЩЕННОГО УМНОЖЕНИЯ
- (2 a – 1) 2 – 4a 2 =
- 4a (a – 2) – (a – 2) 2 + 4 =
- (a + 2)(a + 4) – (a + 1) 2 =
- (a – 1) 2 – (a + 1)(a + 2) =
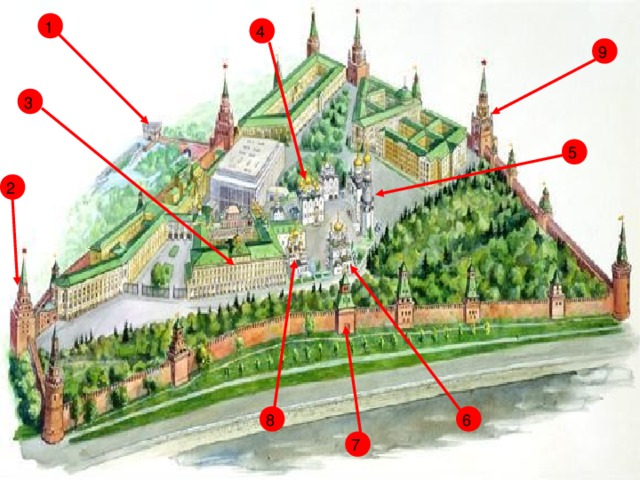
- Рассмотрите схему Московского Кремля. Некоторые объекты на ней обозначены номерами. Узнайте названия этих архитектурных памятников и подпишите их на схеме.
- Для этого разложите на множители выражения. Учитывая найденные ответы и данные таблицы, узнайте, каким номерам какие названия архитектурных памятников соответствуют:
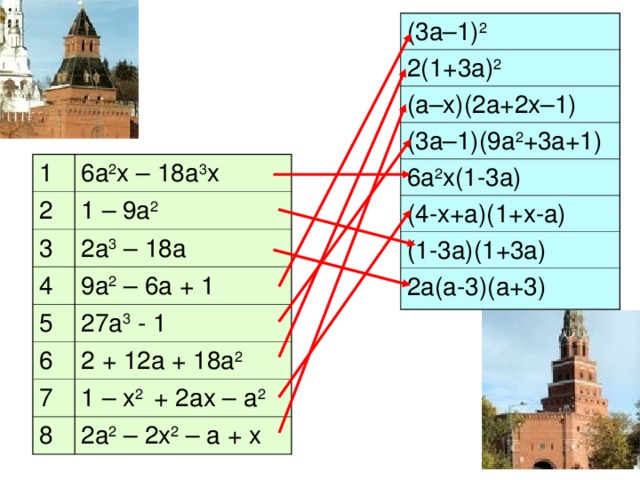
(3a–1) 2
2(1+3 a ) 2
(a–x)(2a+2x–1)
(3a–1)(9a 2 +3a+1)
6a 2 x(1-3a)
(4-x+a)(1+x-a)
(1-3a)(1+3a)
2a(a-3)(a+3)
1
6a 2 x – 18a 3 x
2
1 – 9a 2
3
4
2a 3 – 18a
9a 2 – 6a + 1
5
6
27a 3 - 1
2 + 12a + 18a 2
7
8
1 – x 2 + 2ax – a 2
2a 2 – 2x 2 – a + x
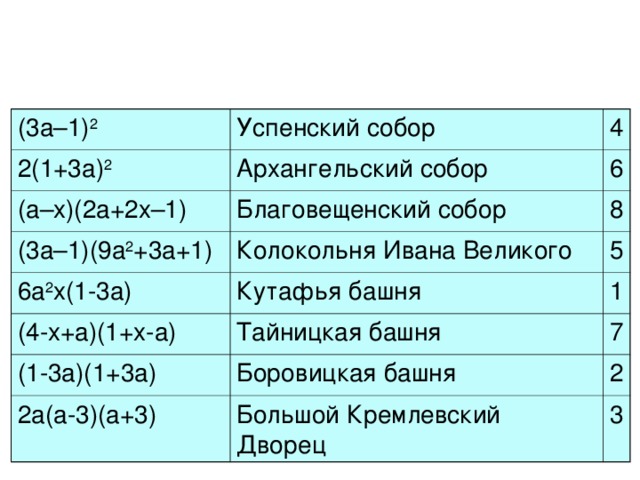
(3a–1) 2
Успенский собор
2(1+3 a ) 2
4
Архангельский собор
(a–x)(2a+2x–1)
Благовещенский собор
(3a–1)(9a 2 +3a+1)
6
6a 2 x(1-3a)
Колокольня Ивана Великого
8
Кутафья башня
5
(4-x+a)(1+x-a)
1
Тайницкая башня
(1-3a)(1+3a)
Боровицкая башня
7
2a(a-3)(a+3)
2
Большой Кремлевский Дворец
3
1
4
9
3
5
2
8
6
7
- Башни Кутафья, Тайницкая, Боровицкая
- Успенский собор
- Архангельский
- Благовещенский
- Ансамбль колокольни Ивана великого
Получите свидетельство
Вход
Формулы сокращённого умножения (2.61 MB)
0
1372
253
Нравится
0
