Формула бинома Ньютона

Формула бинома Ньютона

• Долгое время считалось, что для натуральных показателей степени эту формулу, как и треугольник, позволяющий находить коэффициенты, изобрёл Блез Паскаль, описавший её в XVII веке. Однако историки науки обнаружили, что формула была известна ещё китайскому математику , жившему в 13 веке, а также исламским математикам (13 век) . В середине 16 века Михаэль Штифель описал биномиальные коэффициенты и также составил их таблицу до степени 18.
• Исаак Ньютон около 1677 года обобщил формулу для произвольного показателя степени (дробного, отрицательного и др.). Из биномиального разложения Ньютон, а позднее и Эйлер, выводили всю теорию бесконечных рядов.

Биномиальные коэффициенты

• Формулу (1) обычно называют формулой бинома Ньютона (бином — двучлен), а коэффициенты

биномиальными коэффициентами.

• Известно, что (а + b) 2  = а 2  + 2аb + b 2 .
• Умножив обе части этого тождества на (а + b), получим: (а + b) 3 = (а 2  + 2аb + b 2 )(а + b) = = а 3  + За 2 b + Заb 2  + b 3 . Аналогично умножив обе части тождества (а + b) 3  = а 3 + За 2 b + Заb 2  + b 3  на (а + b), получим: (а + b) 4  = (а 3  + За 2 b + 3 аb 2  + b 3 )(а + b) = а 4  + 4а 3 b + 6а 2 b 2  + 4аb 3  + b 4 .
• Итак,

(а + b) 1  = а + b;

(а + b) 2  = а 2  + 2аb + b 2 ;

(а + b) 3  = а 3  + За 2 b + 3аb 2  + b 3 ;

(а + b) 4  = а 4  + 4а 3 b + 6а 2 b 2  + 4аb 3  + b 4 .

Проанализируем полученные формулы

• Замечаем, во-первых, что в правой части любой из формул сумма показателей при переменных в каждом одночлене равна показателю двучлена в левой части. Например , в последней формуле двучлен возводится в четвертую степень и сумма показателей при а и b в каждом слагаемом в правой части равна 4. Впрочем, это понятно, ведь (а + b) 4  — это (а + b)(а + b)(а + b)(а + b) и после раскрытия скобок получится многочлен, состоящий из одночленов а 4 , а 3 b, а 2 b 2 , аb 3 , b 4  с некоторыми коэффициентами.
• Замечаем, во-вторых, что коэффициенты при одночленах в правых частях формул ассоциируются с треугольником Паскаля, о котором мы говорили в § 52. Сравните числа, имеющиеся в первых четырех строках треугольника, с соответствующими коэффициентами при одночленах в каждой из четырех формул. Полное совпадение.

Свойства биномиальных коэффициентов:

• Для коэффициентов бинома Ньютона справедливы следующие свойства:
• коэффициенты, равноудаленные от начала и конца разложения, равны между собой p=0,1,2,…,n;
• сумма биномиальных коэффициентов равна числу 2, возведенному в степень, равную показателю степени бинома Ньютона.
• сумма биномиальных коэффициентов, стоящих на четных местах, равна сумме биномиальных коэффициентов, стоящих на нечетных местах.
• Первые два свойства являются свойствами числа сочетаний.

Доказательство

(x + a1)(x + a2)...(x + an) Открыв скобки, получим:

( x  +  a 1 )( x  +  a 2 )...( x  +  a n ) =  x n  + ( a 1  + a 2  +...  + a n ) x n- 1 +  + ( a 1 a 2  +  a 2 a 3  +...  +a n- 1  a n ) x n- 2 + ... +  a 1 a 2 ... a n

Коэффициент при  x n- 1 является суммой всевозможных сочетаний из элементов  a 1 a 2 ... a n  по одному элементу, поэтому число слагаемых равно 

  Коэффициент у  x n- 2 является суммой произведений элементов всевозможных сочетаний из тех же элементов  a 1 a 2 ... a n  по два элемента, а следовательно, число слагаемых равно  

Вообще, коэффициент  x k , является суммой произведений элементов всевозможных сочетаний из элементов  a 1 a 2 ... a n  по  k  элементов, и поэтому число таких слагаемых равно 

  Если  a 1  = a 2  =...  = a n  =  a , то из формулы следует, что

( x  +  a ) n  =  x n  +

ax n- 1 +

a 2 x n- 2 + ... +

a n- 1 x n  +  a n ,

формула  доказана .

Свойство биномиальных коэффициентов

• В заключение получим одно любопытное свойство биномиальных коэффициентов. Составим формулу бинома Ньютона для выражения (х + 1) n  (подобно тому, как в рассмотренном примере мы применили формулу бинома Ньютона к выражению (х + I) 6 ). Получим:

Пример 2

Раскрыть скобки в выражении:

а) (x + 1) 6 ;

б) (а 2  - 2b) 5 .

Решение :

а) Применим формулу (1), считая, что а = x, b= 1, n = 6 . Получим:

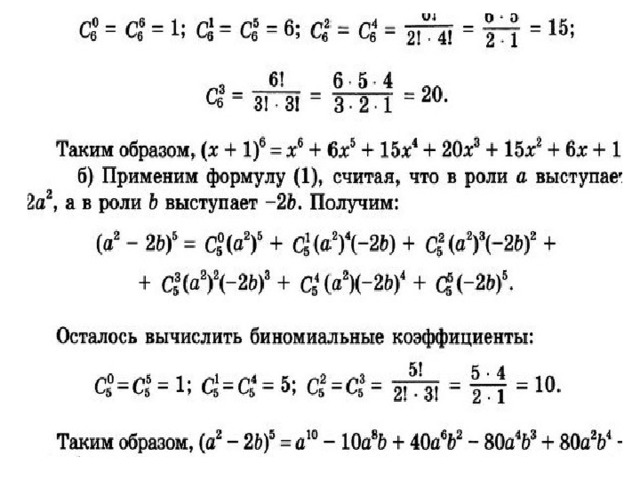
Задача. Пять девушек и трое юношей играют в волейбол. Сколькими способами они могут разбиться на две команды по четыре человека, если в каждой команде должно быть хотя бы по одному юноше?

Решение. Понятно, если мы отберём одну команду из четырёх человек, то вторая определится автоматически. Сколькими способами можно выбрать четыре человека из восьми, чтобы в ней были один или два юноши. Посчитаем команды 1-го типа (содержащие одного юношу). Одного юношу из трёх можно выбрать

способами, трёх девушек из 5 можно выбрать способами. По принципу произведения число команд 1 типа равно

Аналогично, команд второго типа (содержащих двух юношей) существует . Но при таком подсчёте каждое разбиение на команды учитывалось дважды (подумайте почему). Поэтому окончательный ответ: трёх юношей и четырёх девушек можно разбить на две команды, удовлетворяющие условию задачи, 30-ю способами.