ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Элективный курс по предпрофильной подготовке учащихся 9 классов посвящен систематическому изложению учебного материала, связанного с понятием модуля числа и аспектами его применения. В нем рассматриваются различные методы решения уравнений и неравенств с модулем, основанные на его определении, свойствах и графической интерпретации. Значительное внимание уделено вопросам приложения модуля к преобразованиям корней и алгоритмам построения графиков, содержащих модуль.
Для курса характерна практическая направленность. Его основное содержание составляют учебные задачи.
Предлагаемый курс своим содержанием сможет привлечь внимание учащихся, которым интересна математика. Данный элективный курс направлен на расширение знаний учащихся, повышение уровня математической подготовки через решение большого класса задач. Стоит отметить, что навыки в решении уравнений, неравенств, содержащих модуль, и построение графиков элементарных функций, содержащих модуль, совершенно необходимы любому ученику, желающему хорошо подготовиться к поступлению в дальнейшем в высшие учебные заведения и успешно выступать на математических конкурсах и олимпиадах. Наряду с основной задачей обучения математики – обеспечением прочного и сознательного овладения учащимися системой математических знаний и умений, данный курс предусматривает формирование устойчивого интереса к предмету, выявление и развитие математических способностей, ориентацию на профессии, существенным образом связанные с математикой. Таким образом, элективный курс «Алгебра модуля» направлен на подготовку школьников к обучению в классах физико-математического профиля.
Цели курса:
– помочь повысить уровень понимания и практической подготовки в таких вопросах, как: а) преобразование выражений, содержащих модуль; б) решение уравнений и неравенств, содержащих модуль; в) построение графиков элементарных функций, содержащих модуль;
– создать в совокупности с основными разделами курса базу для развития способностей учащихся;
– помочь осознать степень своего интереса к предмету и оценить возможности овладения им с точки зрения дальнейшей перспективы.
Задачи курса:
– научить учащихся преобразовывать выражения, содержащие модуль;
– научить учащихся решать уравнения и неравенства, содержащие модуль;
– научить строить графики, содержащие модуль;
– помочь овладеть рядом технических и интеллектуальных умений на уровне свободного их использования;
– помочь ученику оценить свой потенциал с точки зрения образовательной перспективы.
Данный курс рассчитан на 16 часов и предназначен для изучения в 9 классе. Он предполагает компактное и четкое изложение теории вопроса, решение типовых задач, самостоятельную работу. Разнообразный дидактический материал дает возможность отбирать дополнительные задания для учащихся разной степени подготовки: уровень сложности задач варьируется от простых до конкурсных и олимпиадных. Все занятия направлены на развитие интереса школьников к предмету, на расширение представлений об изучаемом материале, на решение новых и интересных задач.
Основные формы организации учебных занятий: лекция, объяснение, практическая работа, семинар, творческие задания.
В результате изучения курса учащиеся должны уметь:
– точно и грамотно формулировать теоретические положения и излагать собственные рассуждения в ходе решения заданий;
– применять изученные алгоритмы для решения соответствующих заданий;
– преобразовывать выражения, содержащие модуль;
– решать уравнения и неравенства, содержащие модуль;
– строить графики элементарных функций, содержащих модуль.
Изучение данного курса заканчивается проведением итоговой контрольной работы.
Программа создана на основе учебно-методической, справочной литературы.
УЧЕБНО-ТЕМАТИЧЕСКИЙ ПЛАН
| № | Наименование тем курса | Всего часов | В том числе | Форма конт-роля | ||
| Лек-ция | Прак-тика | Семи-нар | ||||
| 1 | Определение модуля числа и его применение при решении уравнений | 1 | 0,5 | 0,5 |
|
|
| 2. | Метод интервалов при решении уравнений и неравенств, содержащих модуль. | 2 |
| 2 |
| С.р. |
| 3 | Решение неравенств вида посредством равносильных переходов. |
1 |
|
1 |
| С. р. |
| 4 | Свойства модуля. Применение свойств модуля при решении уравнений и неравенств |
2 |
0,5 |
1,5 |
|
|
| 5 | Решение уравнений и неравенств с модулями на координатной прямой | 1 |
|
|
|
|
| 6 | Решение уравнений и неравенств с модулями различными способами. |
2 |
|
2 |
1 | Пр. р. |
| 7. | Модуль и преобразование корней. | 2 |
| 2 |
|
|
| 8. | Модуль и иррациональные уравнения. | 1 |
| 1 |
|
|
| 9. | Графики функций, содержащих модуль | 2 | 0.5 | 1.5 |
| С.р. |
| 10. | Модуль в заданиях единого государственного экзамена | 1 |
| 1 |
|
|
| 11. | Итоговая контрольная работа. | 1 |
|
|
| К.р. |
|
| Итого | 16 |
|
|
|
|
СОДЕРЖАНИЕ ПРОГРАММЫ
Тема 1. Определение модуля числа и его применение при решении уравнений.
Определение модуля числа (геометрическая и аналитическая интерпретации). Уравнения, решаемые с помощью определения модуля числа.
Методы обучения: лекция, объяснение, выполнение тренировочных упражнений.
Формы контроля: проверка самостоятельно решенных задач.
Тема 2. Метод интервалов при решении уравнений и неравенств, содержащих модуль.
Раскрытие модулей. Метод интервалов при решении уравнений и неравенств с модулем. Теорема о знакопостоянстве функции. Примеры решения уравнений и неравенств с помощью метода интервалов.
Методы обучения: объяснение, выполнение тренировочных упражнений.
Формы контроля: проверка самостоятельно решенных задач.
Тема 3. Решение неравенств вида посредством равносильных переходов.
Решение неравенств вида посредством равносильных переходов к совокупности или системе неравенств. Самостоятельная работа.
Методы обучения: объяснение, выполнение тренировочных упражнений.
Формы контроля: проверка самостоятельно решенных задач.
Тема 4. Свойства модуля. Применение свойств модуля при решении уравнений и неравенств.
Свойства модуля числа. Примеры применения свойств модуля числа при решении уравнений, неравенств.
Методы обучения: лекция, объяснение, выполнение тренировочных упражнений.
Формы контроля: проверка самостоятельно решенных задач.
Тема 5. Решение уравнений и неравенств с модулями на координатной прямой.
Неравенства вида |x| и |x| a, их геометрическая интерпретация. Примеры неравенств, решаемых с помощью определения модуля числа.
Методы обучения: объяснение, выполнение тренировочных упражнений.
Формы контроля: проверка самостоятельно решенных задач.
Тема 6. Решение уравнений и неравенств с модулями различными способами.
Решение уравнений и неравенств, содержащих модуль в модуле. Метод замены переменной. Решение систем уравнений и неравенств, содержащих модуль. Проверочная работа.
Методы обучения: беседа, объяснение, выполнение тренировочных упражнений.
Формы контроля : проверка самостоятельно решенных задач.
Тема 7. Модуль и преобразование корней.
Применение понятия модуля числа и его свойств при преобразовании выражений. Тождество .
Методы обучения: объяснение, выполнение тренировочных упражнений.
Формы контроля: проверка самостоятельно решенных задач.
Тема 8. Модуль и иррациональные уравнения.
Решение иррациональных уравнений заменой их на равносильные уравнения с модулем.
Методы обучения: выполнение тренировочных упражнений.
Формы контроля: проверка самостоятельно решенных задач.
Тема 9. Графики функций, содержащих модуль.
Построение графиков функций вида .
Построение графиков уравнений и |у| = |f(х)|.
Самостоятельная работа.
Методы обучения: лекция, объяснение, выполнение тренировочных упражнений.
Формы контроля: проверка самостоятельно решенных задач.
Тема 10. Модуль в заданиях единого государственного экзамена
Решение заданий единого государственного экзамена, содержащих модуль.
Методы обучения: выполнение тренировочных упражнений.
Формы контроля: проверка самостоятельно решенных задач .
Литература
Литература для учителя
1. Вавилов, В. В., Мельников, И. И., Олехник, С. Н., Пасиченко, П. И. Задачи по математике. Уравнения и неравенства: справочное пособие. – М.: Наука, 1987.
2. Галицкий, М. Л., Гольдман, А. М., Звавич, Л. И. Планирование учебного материала для 8 класса с углубленным изучением математики: методическое пособие. – М., 1988. – 78 с.
3. Галицкий, М. Л. и др. Сборник задач по алгебре для 8–9 классов: учебн. пособие для учащихся и классов с углубленным изучением математики. – 3-е изд. – М.: Просвещение 1995. – 217 с.
4. Данкова И.Н., Бондаренко Т.Е. Предпрофильная подготовка учащихся 9 классов по математике.- М: «5 за знания», 2006.-128с.
5. Егерман, Е. Задачи с модулем. 9–10 классы // Математика. – № 23. – 2004. – С. 18–20.
6. Егерман, Е. Задачи с модулем. 10–11 классы // Математика. – № 25–26. – 2004. – С. 27–33.
7. Егерман, Е. Задачи с модулем. 10–11 класс // Математика. – № 27–28. – 2004. – С. 37–41.
8. Звавич, Л. И., Шляпочник, Л. Я., Чинкина, М. В. Алгебра и начала анализа. 8–11 кл.: пособие для школ с углубленным изучением математики. – М.: Дрофа, 1999. – 352 с.
9. Садыкина, Н. Построение графиков и зависимостей, содержащих знак модуля // Математика. – № 33. – 2004. – С. 19–21.
10. Сканави, М. И. Сборник задач по математике для поступающих во втузы. – С.-Петербург, 1995.
11. Скворцова, М. Уравнения и неравенства с модулем. 8–9 классы // Математика. – № 20. – 2004. – С. 17.
12. Столин, А.В. Комплексные упражнения по математике с решениями. 7-11 классы. – Х.: ИМП «Рубикон», 1995. – 240 с.
Литература для учащихся
1. Аверьянов, Д. И., Алтынов, П. И. Математика: большой справочник для школьников и поступающих в вузы. – 2-е изд. – М.: Дрофа, 1999. – 864 с.
3. Виленкин, H. Я, Виленкин, Л. Н., Сурвилло, Г. С. и др. Алгебра. 8 класс: учебн. пособие для учащихся и классов с углубленным изучением математики. – М.: Просвещение, 1995. – 256 с.
4. Виленкин, Н. Я., Сурвилло, Г. С., Симонов, А. С., Кудрявцев, А. И. Алгебра. 9 класс: учебн. пособие для учащихся школ и классов с углубленным изучением математики. – М.: Просвещение, 1996. – 384 с.
5. Галицкий, М. Л. и др. Сборник задач по алгебре для 8–9 классов: учебн. пособие для учащихся и классов с углубленным изучением математики. – 3-е изд. – М.: Просвещение 1995. – 217 с.
6. Карп, А. П. Сборник задач по алгебре для учащихся 8–9 классов школ с углубленным изучением математики. – С.-Пб.: Образование, 1993.
Дидактические материалы
Упростить выражения:
№ 1. ![]() .
.
№ 2. ![]() .
.
№ 3. ![]() .
.
№ 4. ![]() .
.
№ 5. ![]() .
.
№ 6. ![]() .
.
№ 7*. 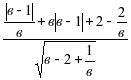 .
.
№ 8. ![]() .
.
№ 9. ![]() .
.
№ 10. ![]() .
.
№ 11. 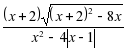 .
.
№ 12. ![]() .
.
№ 13. 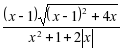 .
.
№ 14. ![]() .
.
№ 15. ![]() .
.
№ 16. ![]() .
.
№ 17. ![]() .
.
№ 18. Доказать, что данное выражение – целое число.
а) ![]() ;
;
б) ![]() ;
;
в) ![]() .
.
№ 19. Вычислите:
а) ![]() ;
;
б) ![]() ;
;
в) ![]() ;
;
г) ![]() ;
;
д) ![]() ;
;
е) ;
ж) .
№ 20. Решить уравнения:
а) |x – 3| = 5.
б) |x + 4| + 1 = 0.
в) |3x + 2| – 4 = 0.
г) ||2x – 5| – 3| = 2.
д) |x2 – 2х –1| = 2.
№ 21. Решить уравнения:
а) |x – 2| + |x + 3| = 7. О т в е т: {–4; 3}.
б) |x – 5| – |x – 2| = 3. О т в е т: 2; +∞).
в) 3|x – 1| – 2|x – 2| + |x + 3| = 2. О т в е т: –3; 1].
г) |x| + 3|x + 2| = 2|x + 1|. О т в е т: –2.
№ 22. Решить уравнения:
а) |2x – 3| = 3 – 2х. О т в е т: .
б) |4 – 5x| = 5х – 4. О т в е т:.
в) |3x – 5| = 5 – 3х. О т в е т: .
г) |7 – 4x| = 7 – 4х. О т в е т: .
№ 23. Решить уравнения:
а) |x3 + 3х2 + х| = –х + х3. О т в е т: .
б) |х2 – 4| = х2 – 4. О т в е т: х ≤ –2; х ≥ 2.
в) |x2 + х – 3| = х. О т в е т: .
№ 24. Решить уравнения:
а) . О т в е т:
.
б) |x2 + х + 1| = 1. О т в е т: –1; 0.
в) . О т в е т:
.
г) |x2 – х – 2| = |2x2 – х – 1|. О т в е т: .
д) |3 – |2 – |1 – x||| = 2. О т в е т: –6; –2; 0; 2; 4; 8.
е) . О т в е т:
.
ж) |x2 – 3х| = x2 – 2х. О т в е т: ; 0.
з) ||х| – 2| = 1 – 2х. О т в е т: .
№ 25. Решить уравнения:
1) |3x2 + 7х – 3| = 3x2 + 3х – 1. О т в е т: 0,5; –2; .
2) |x2 – 4х – 1| = x2 + 6х + 1. О т в е т: 0; –0,2.
3) |3x2 + х – 7| = 3x2 – 3х – 1. О т в е т: 1,5; –1; .
4)* . О т в е т: {–2; 2}.
№ 26. Решить неравенства:
а) |3х + 2| + х 1. О т в е т:
.
б) |х – 1| ≤ 2х + 1. О т в е т: [0; +∞).
в) |х2 – 2| ≤ х. О т в е т: [1; 2].
г) . О т в е т: (–∞; –1)
.
№ 27. Решить неравенства:
а) |4х – 1| + 2х – 4 ≤ 0. О т в е т: .
б) |3 – х| – |х – 2| ≤ 5. О т в е т: (–∞; +∞).
в) |2х – 6| + |4 – х| ≤ |х – 2|. О т в е т: [3; 4].
г) |х2 + 2х| + |х – 2| 4. О т в е т: (–∞; –1) (1; +∞).
д) |х – 4| + | х – 3|. О т в е т:
.
№ 28. Решить неравенства:
1) О т в е т: (–∞; 1) (4; +∞).
2)
3) О т в е т:
.
4)
5) О т в е т:
.
№ 29. Решить неравенства:
1) |х2 + 9х + 5| ≤ |3х2 + 22х + 16|.
О т в е т: (–∞; –7] [–5,5; –1] [; +∞).
2) |х2 + 3х – 5| ≤ |х2 + 7х – 9|.
О т в е т: []
[
).
3) |х2 + 7х – 3| ≥ |3х2 + 16х – 3|. О т в е т: [–6; –4,5] .
№ 30. Решить неравенства:
1) |13 – 2х| ≥ |4х – 9|.
2) |2х + 3| х| – 4х – 1.
3) |х – 1| + |х + 3| ≤ 6.
4) |х – 6| ≤ |х2 – 5х + 2|.
№ 31. Построить графики функций:
у = 3 – 1,5|х|.
у = 1 – |х|.
у = 2|х – 3|.
у = |х + 2| + 1.
у = |2 |х| – 3|.
у = |х + 2| + |х – 1| – |х – 3|.
у = |3х – 4| – х.
у = х – 1 – |х – 1|.
у = .
у = .
у = |х – 1| + |х + 1|.
у = |х – 2| – |х + 2|.
у = |х – 3| + |2х – 1|.
у = |х + 3| + |2х + 1| – х.
.
№ 32. Построить график функции:
а) у = х2 + 2|х| – 3.
б) у = |х2 + 2х – 3|.
в) у = |х2 + 2|х| – 3|.
г) у = |х| ·х + 2х – 3.
№ 33. Построить график функции:
а) у = х2 + 4|х| – 5.
б) у = |х2 + 4х – 5|.
в) у = |х2 + 4|х| – 5|.
г) у = х ·|х| + 4х – 5.
№ 34. Построить графики функций:
а) f(x) = |–x2 + 2x + 3|.
б) f(x) = |x2 – 2x – 3|.
в) f(x) = |x + 1|·|x – 3|.
г) f(x) = |x + 1|·|x – 5|.
д) f(x) = .
№ 35. Построить графики функций:
а) f(x) = | x2 – 2|x| – 3|.
б) f(x) = | x2 – 2|x| – 3| – 2.
в) f(x) = –| x2 – 4|x| – 5|.
г) f(x) = |(|x| – 2)|x| – 3|.
д) f(x) = |(|x| + 1)·||x| – 5|.
e) f(x) = |x|·x – 4x – 5.
ж) f(x) = | x2 – x – 2| – 3(х + 1).
з) f(x) = | 3 – x2| – 2x.
и) f(x) = |x|·|x – 4| – 5.
к) f(x) = ||x|·x – 5| – 4|x|.
№ 36. Построить графики функций:
а) .
б) .
в) .
г) .
д) .
е) .
ж) .
з) .
и) .
к) .
л) .
м) .
н) .
№ 37. Построить графики функций:
а) .
б) .
в) .
г) .
№ 38. Для каждого значения с укажите число корней уравнения:
а) 4х·|x| –х2 – 15х = с;
О т в е т: если с с 18,75, один корень; два корня при с = –11,25; 18,75, три корня –11,25 с
б) 2х·|x| + х2 – 6х = с;
О т в е т: один корень при с с 9; два корня при с = –3; 9; три корня –3 с
в) 3х·|x| + х2 – 8х = с;
О т в е т: один корень при с с 8; два корня при с = –4; 8; три корня при –4 с
№ 39. Построить графики уравнений:
1) |y| = x 5) .
2) |y| = x – 3. 6) .
3) |y| = x + 2. 7) .
4) |y| = |2x + 3|. 8) .
№ 40. При каких значениях параметра а число корней уравнения ||x2 – 2x| – 7| = a в четыре раза больше а?
№ 41. Решить уравнение .
№ 42.Решите уравнение .
№ 43.При каких значениях х функция у = |2x + 3| + 3|x – 1| – |x + 2| имеет наименьшее значение. Найдите это значение.
№ 1. Решить уравнения:
а) |x – 2| + |x + 3| = 7.
б) 3|x – 1| – 2|x – 2| + |x + 3| = 2.
№ 2. Решить уравнения:
а) |2x – 3| = 3 – 2х.
б) |4 – 5x| = 5х – 4.
в) б) |х2 – 4| = х2 – 4.
№ 3. Решить уравнения:
а) |x3 + 3х2 + х| = –х + х3.
в) |x2 + х – 3| = х.
г) |x2 – х – 2| = |2x2 – х – 1|.
д) |3 – |2 – |1 – x||| = 2.
е) |3x2 + 7х – 3| = 3x2 + 3х – 1.
ж) |x2 – 4х – 1| = x2 + 6х + 1.
№ 4. Решить неравенства:
а) |3х + 2| + х 1.
б) |х – 1| ≤ 2х + 1.
в) |х2 – 2| ≤ х.
г) .
№ 5. Решить неравенства:
а) |4х – 1| + 2х – 4 ≤ 0.
б) |3 – х| – |х – 2| ≤ 5.
в) |2х – 6| + |4 – х| ≤ |х – 2|.
г) |х2 + 2х| + |х – 2| 4.
№ 6. Решить неравенства:
1)
2)
3)
4) |13 – 2х| ≥ |4х – 9|.
№ 7. Построить графики функций:
а) у = |2 |х| – 3|.
б) у = |х + 2| + |х – 1| – |х – 3|.
в) у = |3х – 4| – х.
г) у = х – 1 – |х – 1|.
д) у = .
е) у = .
ж) у = |x|·x – 4x – 5.
№ 8. Построить графики функций:
а) .
б) .
в) .
г) .
д) .
е) .

 Получите свидетельство
Получите свидетельство Вход
Вход











 Элективный курс "Алгебра модуля" (84.19 KB)
Элективный курс "Алгебра модуля" (84.19 KB)
 0
0 955
955 114
114 Нравится
0
Нравится
0


