Цели:
систематизировать изученное;
обобщить знания учащихся о тригонометрии;
отработать умение применять формулы, при решении заданий;
корректировать знания и умения учащихся;
развивать интерес к предмету;
развивать личностные качества учащихся;
расширять кругозор и пополнять словарный запас;
развивать навыки самоконтроля;
развивать правильную самооценку.
Продолжительность: 45 мин.
Оборудование: Видеопроектор, экран, презентация, доска, мел, карточки
Ход урока:
1. Организационный момент.
Речи учителя сопутствуют слайды из презентации.
Учитель объявляет эпиграф к уроку, ставит цели для учащихся. (слайд 1,2)
Эпиграф к уроку
Величие человека – в его способности мыслить.
Б. Паскаль
Постановка цели урока для учащихся
Повторение, обобщение знаний по теме «Элементы тригонометрии»
Развитие интереса к изучению математики
Занимательная страничка. Блез Паскаль (19 июня 1623—19 августа 1662) французский математик, физик, литератор и философ. Классик французской литературы, один из основателей математического анализа, теории вероятностей и проективной геометрии, создатель первых образцов счётной техники, автор основного закона гидростатики.
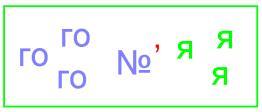
Слово учителя: Когда-то Блез Паскаль сказал, что математика – наука настолько серьёзная, что нельзя упускать случая сделать её немного занимательной. Поэтому я предлагаю наш урок начать с занимательной странички. (учащимся предлагается отгадать ребусы: 1) 144, 2) тригонометрия)
Угадай-ка…(ребусы)
2. Проверка домашнего задания. Учащимся предлагается узнать немного об истории возникновения науки «Тригонометрии» рассказ учащихся. 2 учащихся рассказывают.
3. Повторение изученного материала: слайд
Блиц-опрос
1. Какие знаки в координатных четвертях имеет тригонометрическая функция у= cosa?
2.Сформулировать теорему косинусов.
3.Сформулировать теорему синусов.
4. Что называется радианом?
5. Дать определение синуса, косинуса, тангенса и котангенса.
6. Выразите tgа через соs , ctg через sin
7. Найди пары
Какие части формул соответствуют друг другу?
Работа по карточкам. Обмениваются заданиями с соседом по парте. Работа по парам проверяют друг друга. Отмечают в карте.
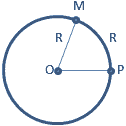
Центральный угол, опирающийся на дугу, длина которой равна радиусу окружности, называется углом в 1 радиан.
Градусная мера угла в 1 радиан равна:
Так как дуга длиной πR (полуокружность), стягивает центральный угол в 180°, то дуга длиной R, стягивает угол в π раз меньший, т.е.
И наоборот
Так как π = 3,14, то 1 рад = 57,3°
Если угол содержит a радиан, то его градусная мера равна. И наоборот.
Обычно при обозначении меры угла в радианах наименование «рад» опускают.
Например, 360° = 2π рад, пишут 360° = 2π
В таблице указаны наиболее часто встречающиеся углы в градусной и радианной мере. 3. Заполнить таблицу.
4. Упростите выражение:
1-sin2a
cos2a-1
sin2a + (1 -cos2a)
Найдите: sina, tga, ctga если известно, что cosa = -2/3 и p/2< a<3p/2
Подведение итогов урока. Выставление оценок.
Подведение итогов урока (рефлекия), проверка карточек учащихся.
5. Домашнее задание
– Подготовить тест на применение тригонометрических формул.
Весь материал - в документе.

 Получите свидетельство
Получите свидетельство Вход
Вход



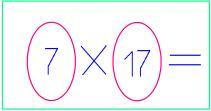
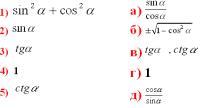









 Элементы тригонометрии (68.68 КB)
Элементы тригонометрии (68.68 КB)
 0
0 979
979 118
118 Нравится
0
Нравится
0







