Экзаменационная работа.

МИНИСТЕРСТВО ОБРАЗОВАНИЯ КРАСНОЯРСКОГО КРАЯ

КРАЕВОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

«КРАСНОЯРСКИЙ АВТОТРАНСПОРТНЫЙ ТЕХНИКУМ»

ИНФОРМАТИКА

23.01.03 «Автомеханик», 23.01.06 «Машинист дорожных и строительных машин», 23.01.07 «Машинист крана (крановщик)»

2016г.

Освоение образовательной программы среднего общего образования завершается обязательным итоговым контролем учебных достижений обучающихся, который проводится в рамках промежуточной аттестации, предусмотренной Федеральными государственными образовательным стандартом среднего профессионального образования (далее – ФГОС СПО)¹.

Итоговый контроль учебных достижений обучающихся при реализации образовательной программы среднего общего образования в пределах ОПОП СПО проводится в форме экзамена.

Экзамены по математике проводится письменно с использованием экзаменационных материалов в виде набора контрольных заданий, требующих полного решения.

Вид и содержание контрольных материалов определяется преподавателем соответствующей учебной дисциплины.

Экзамен проводятся в конце 4-го семестра. Сроки проведения экзаменов устанавливаются образовательным учреждением.

1. Процедура проведения экзамена

На выполнение письменной экзаменационной работы отводится 4 астрономических часа (240 минут).

Перед началом выполнения письменной экзаменационной работы (время не входит в 4 астрономических часа) преподаватель контролирует заполнение личных данных обучающихся, знакомит обучающихся со структурой экзаменационной работы, с критериями оценивания еë результатов.

В экзаменационную работу включаются задания, выполнение которых свидетельствует о наличии общематематических навыков, необходимых человеку в современном обществе. Эти задания должны проверять базовые вычислительные и логические умения и навыки, умение анализировать информацию, представленную в графиках, ориентироваться в простейших геометрических конструкциях.

Задания в экзаменационных работах расположены по нарастанию сложности – от относительно простых до достаточно сложных, подразумевающих свободное владение материалом курса и наличие высокого уровня математического развития.

При составлении экзаменационной работы по математике учитываются следующие требования:

– структурно она составляется из 2-х частей:

Первая часть включает в себя пять заданий по алгебре и началам анализа и два геометрических задания.

Задания первой части не требуют громоздких вычислений, сложных преобразований и нестандартных умозаключений. Для их решения достаточно уметь использовать основные определения, владеть минимальным набором формул и алгоритмов. Задания по геометрии требуют, помимо знания формул и умения ими пользоваться, определенного уровня стереометрических представлений, умения работать с изображениями пространственных конфигураций.

Вторая часть экзаменационной работы состоит из одного геометрического задания и двух заданий по алгебре и началам анализа. Уровень сложности данных заданий несколько выше, чем в первой части.

– текст экзаменационной работы сопровождается критериями оценивания результатов ее выполнения для получения каждой из положительных оценок (3, 4, 5)

– обеспечивается представленность заданий основных содержательных линий учебного курса математики (алгебраической, уравнений и неравенств, теоретико-функциональной, геометрической);

– в заданиях отражаются основные умения и виды деятельности, которые должны быть сформированы при изучении учебного курса математики (в том числе умения использовать приобретенные знания и умения в практической деятельности и повседневной жизни); выполнять вычисления и преобразования; решать уравнения и неравенства; выполнять действия с функциями; выполнять действия с геометрическими фигурами, координатами; строить и исследовать математические модели);

– в формулировках заданий обозначаются конкретные виды деятельности, на выполнение которых направлено соответствующее задание (определите, вычислите, решите, найдите и др.).

К проведению экзамена по математике для каждого обучающегося готовится текст с вариантом экзаменационной работы и критериями оценивания результатов ее выполнения, а также листы для черновика и для чистового оформления работы.

Обучающимся поясняется, что основные требования к выполнению заданий состоят в том, чтобы:

– из представленного решения был понятен ход рассуждений обучающегося;

– ход решения был математически грамотным;

– представленный ответ был правильным.

При этом метод и форма описания решения задачи могут быть произвольными.

2. Проверка экзаменационной работы и оценивание результатов экзамена.

При проверке математической подготовки выпускников оценивается уровень сформированности следующих умений:

• выполнять арифметические действия, сочетая устные и письменные приемы; находить значения корня натуральной степени, степени с рациональным показателем, логарифма;

• проводить по известным формулам и правилам преобразования буквенных выражений, включающих степени, радикалы, логарифмы и тригонометрические функции;

• вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования;

• определять значение функции по значению аргумента при различных способах задания функции;

• строить графики изученных функций; описывать по графику поведение и свойства функций, находить по графику функции наибольшие и наименьшие значения;

• решать уравнения, простейшие системы уравнений, используя графики функций;

• вычислять производные и первообразные элементарных функций;

• исследовать в простейших случаях функции на монотонность, находить наибольшие и наименьшие значения функций, строить графики многочленов с использованием аппарата математического анализа;

• решать рациональные, показательные и логарифмические уравнения и неравенства, простейшие иррациональные и тригонометрические уравнения, их системы;

• анализировать в простейших случаях взаимное расположение объектов в пространстве;

• изображать основные многогранники и круглые тела; выполнять чертежи по условиям задач;

• решать планиметрические и простейшие стереометрические задачи на нахождение геометрических величин (длин, углов, площадей, объемов);

• использовать при решении стереометрических задач планиметрические факты и методы;

• проводить доказательные рассуждения в ходе решения задач.

При оценке экзаменационной работы выпускника используется пятибалльная система. Результаты итогового контроля учебных достижений обучающихся признаются удовлетворительными в случае, если выпускник при сдаче государственного выпускного экзамена по математике получил отметку не ниже удовлетворительной.

Для получения оценки «3» (удовлетворительно) обучающийся должен правильно выполнить любые пять заданий. Оценка «4» (хорошо) выставляется при выполнении любых семи заданий. Оценка «5» (отлично) ставиться за девять верно выполненных заданий.

3. Элементы содержания, проверяемые заданиями экзаменационной работы

Алгебра

Числа, корни и степени

Целые числа

Степень с натуральным показателем

Дроби, проценты, рациональные числа

Степень с целым показателем

Корень степени n 1 и его свойства

Степень с рациональным показателем и ее свойства

Свойства степени с действительным показателем

Основы тригонометрии

Синус, косинус, тангенс, котангенс произвольного угла

Радианная мера угла

Синус, косинус, тангенс и котангенс числа

Основные тригонометрические тождества

Формулы приведения

Синус, косинус и тангенс суммы и разности двух углов

Синус и косинус двойного угла

1 Согласован с «Кодификатором элементов содержания к уровню подготовки выпускников общеобразовательных учреждений для проведения ЕГЭ по математике», подготовленного ФГНУ «Федеральный институт педагогических измерений», 2011.

Логарифмы

Логарифм числа

Логарифм произведения, частного, степени

Десятичный и натуральный логарифмы, число е

Преобразования выражений

Преобразования выражений, включающих арифметические операции

Преобразования выражений, включающих операцию возведения в степень

Преобразования выражений, включающих корни натуральной степени

Преобразования тригонометрических выражений

Преобразование выражений, включающих операцию логарифмирования

Модуль (абсолютная величина) числа

Уравнения и неравенства

Уравнения

Квадратные уравнения

Рациональные уравнения

Иррациональные уравнения

Тригонометрические уравнения

Показательные уравнения

Логарифмические уравнения

Равносильность уравнений, систем уравнений

Простейшие системы уравнений с двумя неизвестными

Основные приемы решения систем уравнений: подстановка, алгебраическое сложение, введение новых переменных

Использование свойств и графиков функций при решении уравнений

Изображение на координатной плоскости множества решений уравнений с двумя переменными и их систем

Применение математических методов для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учет реальных ограничений.

Неравенства

Квадратные неравенства

Рациональные неравенства

Показательные неравенства

Логарифмические неравенства

Системы линейных неравенств

Системы неравенств с одной переменной

Равносильность неравенств, систем неравенств

Использование свойств и графиков функций при решении неравенств

Метод интервалов

Изображение на координатной плоскости множества решений неравенств с двумя переменными и их систем

Функции

Определение и график функции

Функция, область определения функции

Множество значений функции

График функции. Примеры функциональных зависимостей в реальных процессах и явлениях

Обратная функция. График обратной функции

Преобразования графиков: параллельный перенос, симметрия относительно осей координат

Элементарное исследование функций

Монотонность функций. Промежутки возрастания и убывания

Четность и нечетность функций

Периодичность функций

Ограниченность функций

Точки экстремума (локального максимума и минимума) функции

Наибольшее и наименьшее значения функции

Основные элементарные функции

Линейная функция, ее график

Функция, описывающая обратную пропорциональную зависимость, ее график

Квадратичная функция, ее график

Степенная функция с натуральным показателем, ее график

Тригонометрические функции, их графики

Показательная функция, ее график

Логарифмическая функция, ее график

Начала математического анализа

Производная

Понятие о производной функции, геометрический смысл производной

Физический смысл производной, нахождение скорости для процесса, заданного формулой или графиком

Уравнение касательной к графику функции

Производные суммы, разности, произведения, частного

Производные основных элементарных функций

Вторая производная и ее физический смысл

Исследование функций

Применение производной к исследованию функций и построению графиков

Примеры использования производной для нахождения наилучшего решения в прикладных, в том числе социально-экономических, задачах

Первообразная и интеграл

Первообразные элементарных функций

Примеры применения интеграла в физике и геометрии

Геометрия

Планиметрия

Треугольник

Параллелограмм, прямоугольник, ромб, квадрат

Трапеция

Окружность и круг

Окружность, вписанная в треугольник, и окружность, описанная около треугольника

Многоугольник. Сумма углов выпуклого многоугольника

Правильные многоугольники. Вписанные и описанные окружности правильного многоугольника

Прямые и плоскости в пространстве

Пересекающиеся, параллельные и скрещивающиеся прямые;

перпендикулярность прямых

Параллельность прямой и плоскости, признаки и свойства

Параллельность плоскостей, признаки и свойства

Перпендикулярность прямой и плоскости, признаки и свойства;

перпендикуляр и наклонная; теорема о трех перпендикулярах

Перпендикулярность плоскостей, признаки и свойства

Параллельное проектирование. Изображение пространственных фигур

Многогранники

Призма, ее основания, боковые ребра, высота, боковая поверхность; прямая призма; правильная призма

Параллелепипед; куб; симметрии в кубе, в параллелепипеде

Пирамида, ее основание, боковые ребра, высота, боковая поверхность; треугольная пирамида; правильная пирамида

Сечения куба, призмы, пирамиды

Представление о правильных многогранниках (тетраэдр, куб, октаэдр, додекаэдр и икосаэдр)

Тела и поверхности вращения

Цилиндр. Основание, высота, боковая поверхность, образующая, развертка

Конус. Основание, высота, боковая поверхность, образующая, развертка

Шар и сфера, их сечения

Измерение геометрических величин

Величина угла, градусная мера угла, соответствие между величиной угла и длиной дуги окружности

Угол между прямыми в пространстве; угол между прямой и плоскостью

Длина отрезка, ломаной, окружности, периметр многоугольника

Расстояние от точки до прямой, от точки до плоскости; расстояние между параллельными прямыми, параллельными плоскостями

Площадь треугольника, параллелограмма, трапеции, круга, сектора

Площадь поверхности конуса, цилиндра, сферы

Объем куба, прямоугольного параллелепипеда, пирамиды, призмы, цилиндра, конуса, шара

Координаты и векторы

Декартовы координаты на плоскости и в пространстве

Формула расстояния между двумя точками; уравнение сферы

Вектор, модуль вектора, равенство векторов; сложение векторов и умножение вектора на число

Коллинеарные векторы. Разложение вектора по двум неколлинеарным векторам

Компланарные векторы. Разложение по трем некомпланарным векторам

Координаты вектора; скалярное произведение векторов; угол между векторами

Элементы комбинаторики, статистики и теории вероятностей

Элементы комбинаторики

Поочередный и одновременный выбор

Формулы числа сочетаний и перестановок. Бином Ньютона

Элементы статистики

Табличное и графическое представление данных

Числовые характеристики рядов данных

Элементы теории вероятностей

Вероятности событий

Примеры использования вероятностей и статистики при решении прикладных задач

4. Общие требования культуры ведения записей в экзаменационной работе

-Краткое условие задачи (если оно есть в геометрических задачах) отделяется от решения.

-Всякая новая мысль начинается с красной строки.

-Записи ведутся аккуратно, разборчивым почерком, используя шариковую ручку с пастой синего или фиолетового цвета.

-Не допускается использование фломастеров, наклеек, цветных стержней.

-Между номером задания, решением и ответом пропускается одна клетка вниз.

-Построение геометрических фигур, графиков функций, выполнение рисунков осуществляется только с помощью карандаша, линейки и циркуля.

Правильное расположение математических знаков в строке. Так, перенос формулы или выражения с одной строки на другую разрешается производить только на знаках сложения, вычитания, умножения и равенства. При переносе, знаки «+», «-» и «=» повторяются на следующей строке, знак умножения заменяется «х», который тоже повторяется на следующей строке. Правильно располагать черту дроби и знак равенства. Черта дроби не разрывается.

-Сокращение обозначений единиц измерения должно быть правильным.

-Не допустимо сокращение слов в рассуждениях.

-Нельзя слова «следовательно», «значит», «треугольник», «параллельно» и т.д. в тексте заменять математическими знаками.

-В конце решения должен быть обязательно ответ. В задачах на доказательство, исследование или построение – вывод.

-Правильность решения. Решение задачи не должно содержать математических и логических ошибок. Среди математических ошибок различают существенные (грубые) и несущественные (негрубые) ошибки.

При проверке работ следует иметь в виду, что оформление решений может быть разным. Здесь важно, чтобы в записях были видны основные этапы решения и логика. Надо обосновывать все то, что не является очевидным по ходу решения и объяснять дополнительные построения, если они выполняются.

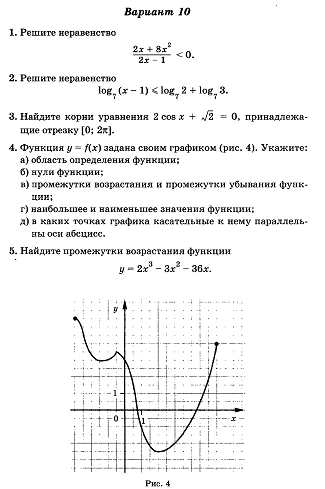
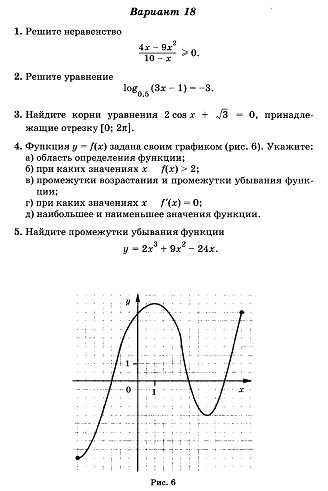
5. Экзаменационная работа по дисциплине «Математика».

Экзаменационная работа составлена в четырех вариантах для групп второго курса по профессиям 23.01.03 «Автомеханик», 23.01.06 «Машинист дорожных и строительных машин».

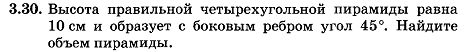
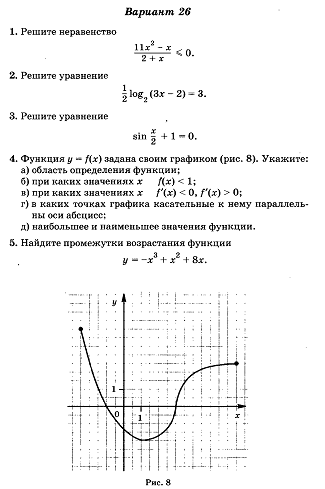
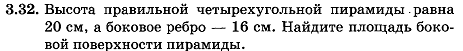
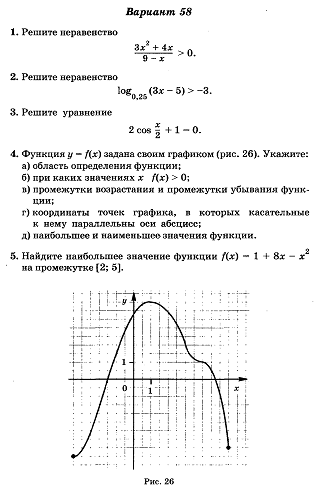
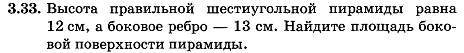
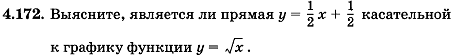
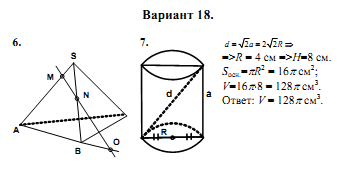
6. Ответы к экзаменационным работам по дисциплине «Математика»

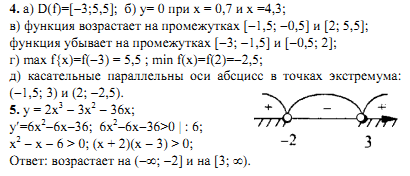
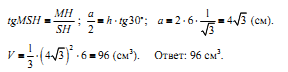
1