Десятичные дроби
И как с ними бороться?
Автор: Родин Николай Васильевич
Учитель математики МОУ «Невонская СОШ №2»
Усть-Илимский район, п. Невон
Вместо предисловия
Дорогой друг!
Это пособие создавалось именно для тебя. Его предназначение – помочь тебе разобраться с десятичными дробями. Сейчас во всех сферах деятельности приходится сталкиваться с такими числами, поэтому каждый образованный человек должен уметь работать с ними. В этом мы тебе и поможем.
Счастливого изучения!
Содержание
- Урок 1. От обыкновенных дробей к десятичным
- Урок 2. Сравним эти дроби!
- Урок 3 . Учимся складывать и вычитать десятичные дроби
На этом уроке мы с тобой узнаем, что такое десятичная дробь, как она появилась, как из обыкновенной дроби получить десятичную. Постарайся не упустить ничего – пропустишь в начале, сложно будет в конце!
Урок 1
От обыкновенных дробей к десятичным
Начать
Урок 1. От обыкновенных дробей к десятичным
- Решим простую задачку
- выразим расстояние 1 дм 6 см в дециметрах.
Решение
1 дм
Чтобы выразить это расстояние в дециметрах, придется использовать дроби.
Так как 1 см = дм , то 6 см = дм
Поэтому 1 дм 6 см = дм
Урок 1. От обыкновенных дробей к десятичным
Числа со знаменателем 10, 100, 1000 и т.д. условились записывать без знаменателя.
Таким же образом можно найти, что
4 ц 17 кг = ц;
13 руб. 8 коп. = руб.
Сначала пишут целую часть , а потом числитель дробной части.
Целую часть отделяют от дробной части запятой .
Например, число пишут 4,17
(читается «4 целых 17 сотых»)
Урок 1. От обыкновенных дробей к десятичным
Появились десятичные дроби в трудах арабских математиков в средние века и независимо от них в древнем Китае. Но и раньше, в древнем Вавилоне, использовали дроби такого же типа, но конечно шестидесятеричные.
Позднее учёный Гартман Бейер (1563-1625) Выпустил сочинение «Десятичная логистика» где писал: «…я обратил внимание на то, что техники и ремесленники, когда измеряют какую-нибудь длину, то очень редко и лишь в исключительных случаях выражают её в целых числах одного наименования; обыкновенно им приходится или брать мелкие меры, или обращаться к дробям, точно так же астрономы измеряют величины не только в градусах, но и в долях градуса, т.е. минутах, секундах и т.п., но мне кажется их деление на 60 частей не так удобно, как деление на 10, на 100 частей и т.д., потому что в последнем случае гораздо легче складывать, вычитать и вообще производить арифметические действия; мне кажется, что десятичные доли, если бы ввести вместо шестидесятеричных, пригодились бы не только для астрономии, но и для всякого рода вычислений.»
В европейскую же практику десятичные дроби ввёл Симон Стевин. До тех пор каждый, кто сталкивался с нецелыми числами, должен был возится с числителями и знаменателями.
Урок 1. От обыкновенных дробей к десятичным
Итак, любое число, знаменатель которой выражается единицей с несколькими нулями, можно представить в виде десятичной дроби .
А если у обыкновенной дроби нет целой части? Как записать ее в виде десятичной?
Если дробь правильная, то перед запятой в десятичной записи пишут 0. Например, = 0,3
(читается «0 целых 3 десятых»)
Урок 1. От обыкновенных дробей к десятичным
Получается, любую дробь со знаменателем 10, 100, 1000 и т.д. можно записать в виде десятичной дроби. То есть,
«4 целых 6 десятых»
«5 целых 34 сотых»
«0 целых 3 десятых»
Интересно. А число 4,5 – это 4 целых 5 десятых или 4 целых 5 сотых? Как определить, сколько нулей в знаменателе?
?
Урок 1. От обыкновенных дробей к десятичным
После запятой числитель дробной части должен иметь столько же цифр , сколько нулей в знаменателе . Поэтому число
сначала надо записать так:
Теперь его можно записать как 7,021 («7 целых 21 тысячная»)
Понял! Значит,
3,08 – это 3 целых 8 сотых
3,8 – это 3 целых 8 десятых
3,008 – это 3 целых 8 тысячных!
Урок 1. От обыкновенных дробей к десятичным
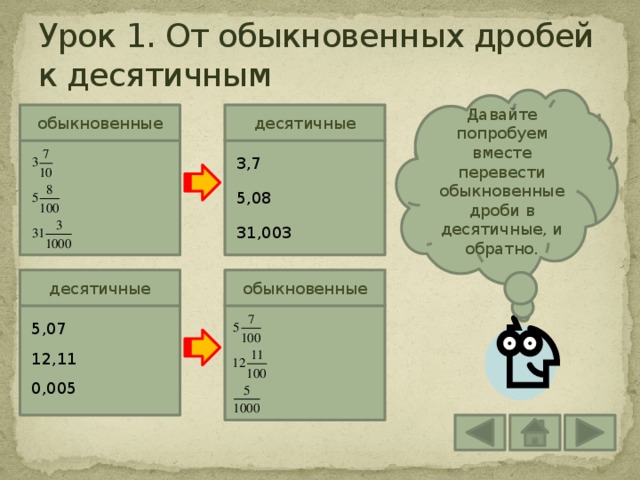
Давайте попробуем вместе перевести обыкновенные дроби в десятичные, и обратно.
десятичные
обыкновенные
3,7
5,08
31,003
обыкновенные
десятичные
5,07
12,11
0,005
Урок 1. От обыкновенных дробей к десятичным
Итак, наш первый урок подошел к концу. Давайте подумаем, чему мы научились?
Во-первых , мы узнали новое понятие – десятичная дробь.
Во-вторых , мы научились правильно читать десятичные дроби.
В-третьих , Мы научились переводить обыкновенные дроби в десятичные, и наоборот.
На этом уроке мы с тобой научимся определять, какая из двух десятичных дробей больше, а какая – меньше, или устанавливать, что они равны. Итак, вперед!
Урок 2
Сравним эти дроби!
Начать
Урок 2. Сравним эти дроби!
Перед тем, как научиться сравнивать десятичные дроби, ты должен
запомнить важное правило десятичных дробей:
Если к десятичной дроби приписать справа нули, то получится равная ей дробь.
Так значит получается, что
3,8 и 3,80 – это равные дроби?
Верно. Получается, что
3,8 = 3,80 = 3,800
0,02 = 0,020 = 0,0200
Урок 2. Сравним эти дроби!
Ну и что? А как же с разными дробями? Как их сравнивать?
А давай сравним, к примеру, два числа:
5,7 и 6,5.
Если переведем эти десятичные дроби в обыкновенные, то получим, что
Значит, 5,7
3,10 " width="640"
Урок 2. Сравним эти дроби!
А как же дроби с разным количеством знаков после запятой?
Хороший вопрос. Давай попробуем сравнить 4,12 и 3,1.
Переведём эти дроби в обыкновенные:
Получились две дроби с разными знаменателями. Чтобы их сравнить, попробуем воспользоваться правилом десятичной дроби. Припишем один нуль ко второй дроби. Получим, что 4,12 3,10
4,51 4,501 0 Сравним два числа: 4,51 и 4,501 Видим, что у первой дроби 2 десятичных Знака, а у второй – 3. Добавим к первой дроби справа один нуль Теперь, не обращая внимания на запятую, сравним эти числа " width="640"
Урок 2. Сравним эти дроби!
Ты, наверное, догадался, как сравнить две десятичные дроби. Итак, правило сравнения двух десятичных дробей:
Чтобы сравнить две десятичные дроби, надо сначала уровнять у них число десятичных знаков, приписав к одной из них справа нули, а потом, отбросив запятую, сравнить получившиеся натуральные числа.
4,51 4,501
0
Сравним два числа: 4,51 и 4,501
Видим, что у первой дроби 2 десятичных
Знака, а у второй – 3.
Добавим к первой дроби справа один нуль
Теперь, не обращая внимания на запятую,
сравним эти числа
= " width="640"
Урок 2. Сравним эти дроби!
Давайте попробуем вместе сравнить пары десятичных дробей.
Сравни пары десятичных дробей:
3,54 3,45
2,222 2,220
0,09 0,091
3,20 3,2
3,033 3, 33
0,002 0,0002
=
Урок 2. Сравним эти дроби!
Вот и подошел к концу второй урок нашего пособия.
Во-первых , мы познакомились с правилом десятичных дробей.
Во-вторых , мы сами вывели правило сравнения десятичных дробей.
В-третьих , Мы научились сравнивать любые десятичные дроби.
На уроках математики ты всегда работаешь с числами – складываешь, вычитаешь, умножаешь и делишь. Десятичные дроби – тоже числа, поэтому необходимо уметь их складывать и вычитать. Этим мы и займемся на третьем уроке.
Урок 3
Учимся складывать и вычитать десятичные дроби.
Начать
Урок 3. Учимся складывать и вычитать десятичные дроби
Итак, как же сложить две десятичные дроби?
Правило сложения и вычитания десятичных дробей:
Чтобы сложить (вычесть) две десятичные дроби, нужно:
- Записать числа друг под другом так, чтобы запятая была под запятой.
- Сложить (вычесть) числа, не обращая внимания на запятую.
- Снести запятую
32 , 876
32 , 876
+
4 , 25
-
4 , 25
,
,
37 126
28 626
Урок 3. Учимся складывать и вычитать десятичные дроби
Проверь себя!
0,769 + 42,389 =
43,158
13,865
13,75 + 0,115 =
8,9021 + 0,68 =
9,5821
9,4 – 7,3 =
2,1
11,1 – 2,8 =
8,3
88,252 – 4,69 =
83,562
ответы
Урок 3. Учимся складывать и вычитать десятичные дроби
Урок третий пройден успешно.
Во-первых , мы познакомились с правилом сложения и вычитания десятичных дробей.
Во-вторых , мы научились складывать десятичные дроби.
В-третьих , мы научились вычитать десятичные дроби.
Получите свидетельство
Вход
Десятичные дроби (0.47 MB)
0
795
63
Нравится
0
