Тема: « Числовые последовательности. Способы задания и свойства числовых последовательностей».
Функции, область определения которых является множеством натуральных чисел или его частью, называются числовыми последовательностями.
Пример:
числовой последовательностью является 1,3,5,7,9...
Числа, записанные в последовательности, называются членами последовательности. Обычно их обозначают маленькими буквами, например, а1,а2,а3...аn…, где индекс 1,2,3,4…n… после буквы а указывает на порядковый номер каждого члена последовательности.
Общий вид последовательности — это (аn), или a1,a2,a3...an...
аn называется общим членом последовательности, или n-м членом, где n — порядковый номер члена последовательности.
У натуральных чисел, считая от 1, десятый член последовательности — это a10=10.
Последовательность возможно задать, указав все её члены или указав общую формулу. Формула показывает, как найти любой член последовательности, если известен порядковый номер n.
Пример:
в последовательности, где общая формула an=3n, написать a) первые четыре члена; b) двадцатый член.
a) Если n=1, то вместо n в формулу подставляется 1: a1=3⋅1=3;
a2=3⋅2=6;
a3=3⋅3=9;
a4=3⋅4=12.
b) Если n=20, то вместо n в формулу подставляется 20: a20=3⋅20=60.
Числовая последовательность бесконечна, если вместо n можно подставлять любые другие натуральные числа (бесконечное множество).
Определение: Функцию y=f(x), x∈N, называют функцией натурального аргумента, или числовой последовательностью, и обозначают: y=f(n), или y1,y2...yn..., или y(n).
Последовательности можно задавать:
1. словесно
— когда правило последовательности описано словами, без указания формулы.
Пример:
последовательность простых чисел: 2,3,5,7,11,13,17,19,23,29,31...
2. аналитически
— когда указана формула её n-го члена.
Пример:
1. yn=n2;
последовательность 1,4,9,16...n2...
Шаги решения: n=1,2,3...
Y1=12=1;y2=22=4;y3=32=9;y4=42=16;y5=...
2. yn=5(yn=C);
последовательность
5,5,5...5...(C,C,C...C...).
Шаги решения:
Y1=5;y2=5;y3=5;y4=...
Последовательность yn=C называют постоянной, или стационарной;
3. рекуррентно
— когда указывают правило, позволяющее вычислить n-й член последовательности, если известны её предыдущие члены.
- Арифметическая прогрессия — (an), заданная рекуррентно соотношениями: a1=a, an+1=an+d.
- Последовательность Фибоначчи — в которой каждое последующее число равно сумме двух предыдущих чисел.
an+1=an+an-1,1,2,3,5,8,13,21,34,55...
4. графически
— график последовательности состоит из точек с абсциссами 1,2,3,4...
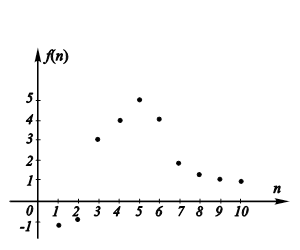
Свойства числовых последовательностей.
Последовательность называется возрастающей, если для любого n∈N выполняется неравенство ann+1.
Последовательность называется убывающей, если для любого n∈N выполняется неравенство ana+n1.
Возрастающие и убывающие последовательности называются монотонными.
Пример:
1. Последовательность, заданная формулой an=n/n+1, является монотонной, возрастающей, т. к. разница an+1−an=n+1/n+2−n/n+1=1/(n+1)⋅(n+2)0, то есть ann+1.
2. Последовательность с общим членом an=1+(−1)n не является монотонной, т. к. a12,a2a3
.
Последовательность называется ограниченной сверху, если существует такое число M∈R, что an≤M. При этом число M называется верхней границей последовательности.
Последовательность называется ограниченной снизу, если существует такое число m∈R, что an≥m. Число m называется нижней границей последовательности.
Пример.
1. последовательность, заданная формулой an=n (1,2,3...n...), ограничена снизу, но не ограничена сверху.
2. Последовательность, заданная формулой an=(−1)n n; (−1,2,−3,4...(−1)n n...), не ограничена ни сверху, ни снизу.
Последовательность называется ограниченной, если она одновременно ограничена и сверху, и снизу.
Тренировочный тест:
1.Запишите первые пять членов последовательности, если общая формула последовательности an =0,7 Ответ: a1; a2; а3; а4; а5?
2.Дана последовательность: 2,3,5,8,13,… Найдите 13-й член этой последовательности (Посмотрите последовательность Фибоначчи).
Ответ:
3.Найдите три первые члена последовательности an=(-1)7n+7n и вычислить их сумму. Ответ: a1; a2; а3? S3=?
4.Вычислите три последующих члена последовательности, если a1=9 и
an=5an-1+4 Ответ: a2; а3; а4
5. Дана последовательность, у которой a1=11,a2=7 и an=5an-2 - an-1.
Определите вид последовательности и вычислите четвертый член последовательности
Ответ:
6.Укажите номер члена последовательности уn=20-n/5n+6, равного17/21. Ответ: ?
Тема «Понятие о пределе последовательности»

Рассмотрим по рисунку две числовые последовательности ( уn ) и (xn).
Замечаем, что члены последовательности (xn) как бы «сгущаются» около точки 0 – говорят последовательность сходятся , а у последовательности (уn) такой точки сгущения нет – и говорят, что последовательность расходится.
Математики не используют термин точка сгущения, а они говорят предел последовательности.
Определение: Число b называется пределом последовательности (xn), если в любой заранее выбранной окрестности точки b содержится все члены последовательности, начиная с некоторого номера.
Пишут так: уn→b или 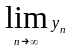 =b
=b
читают так: предел последовательности уn при стремлении n к бесконечности равен b.
На практике используется еще одно истолкование равенства 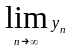 =b, связанное с приближенными вычислениями: если последовательность уn = f(n) сходится к числу b, то выполняется приближенное равенство f(n)≈b, причем это приближенное равенство тем точнее, чем больше n.
=b, связанное с приближенными вычислениями: если последовательность уn = f(n) сходится к числу b, то выполняется приближенное равенство f(n)≈b, причем это приближенное равенство тем точнее, чем больше n.
Иначе:
Возьмём интервал (b−r1;b+r 1 ) т. е. окрестность точки b; r1 — радиус этой окрестности (r10). Существует номер n1, начиная с которого вся последовательность содержится в указанной окрестности: yn1∈(b−r1;b+r1),yn1+1∈(b−r1;b+r1),yn1+2∈(b−r1;b+r1) и т. д.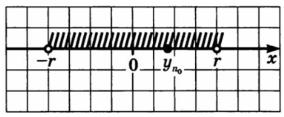
Пример:
дана последовательность (yn): 1,1/2,1/3,1/4...1/n...
Доказать, что 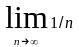 =0.
=0.
Решение.
Возьмём любую окрестность точки 0, пусть её радиус равен r.
Ясно, что всегда можно подобрать натуральное число n0 так, чтобы выполнялось неравенство 1/n0.
Если r=0,001, то в качестве n0 можно взять 1001, поскольку 1/1001, и т. д.
Это значит, что член последовательности (yn) с номером n0, т. е. yn0, попадает в выбранную окрестность точки 0. Тем более, в этой окрестности будут находиться все последующие члены заданной убывающей последовательности yn=1/n. В соответствии с определением это и означает, что 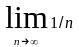 =0.
=0.
Для наглядности построим график последовательности yn=1/n, который состоит из точек с абсциссами 1,2,3,4..., лежащих на ветви гиперболы y=1/x.

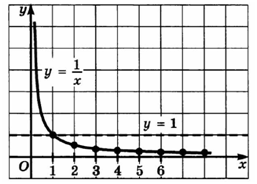
Так как 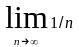 =0, то прямая y=0 является горизонтальной асимптотой графика функции y=1/x,x∈N.
=0, то прямая y=0 является горизонтальной асимптотой графика функции y=1/x,x∈N.
Формулы вычисления пределов последовательностей:
Необходимое условие сходимости произвольной числовой последовательности:
Для того чтобы последовательность сходилась, необходимо, чтобы она была ограниченной.
Достаточное условие сходимости последовательности.
Если последовательность монотонна и ограничена, то она сходится. (теорема К.Вейерштрасса)
Свойства сходящихся последовательностей
1.Если последовательность сходится, то только к одному пределу.
2.Если последовательность сходится, то она ограничена.
3. Если последовательность монотонна и ограничена, то она сходится.
Если |q|1, то последовательность уn= qn расходится.
Приведём классический пример из геометрии, в котором используется теорема Вейерштрасса.
Возьмём окружность и будем последовательно вписывать в неё правильные многоугольники:
4-угольник, 8-угольник, 16-угольник и т. д. Последовательность площадей этих правильных многоугольников возрастает и ограничена (снизу числом 0, а сверху, например, числом, выражающим площадь описанного около окружности квадрата).
Значит, построенная последовательность сходится, её предел принимается за площадь круга.
Именно с помощью таких рассуждений и получена в математике формула площади круга S=πr2.
Теоремы о пределах последовательностей.
1. 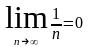
2. Если 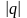 1, то
1, то 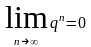
Если xn=b ,
xn=b ,  yn=c, то
yn=c, то
3.Для любого натурального показателя m и любого коэффициента k справедливо соотношение: 
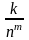 =0
=0
4.Предел суммы равен сумме пределов:
 ( xn+ yn ) =
( xn+ yn ) = xn+
xn+  yn = =b+c
yn = =b+c
5. Предел произведения равен произведению пределов:
 ( xn
( xn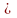 yn ) =
yn ) = xn
xn 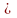
 yn =b
yn =b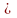 c
c
6.Предел частного равен частному пределов:
 ( x n /yn ) =
( x n /yn ) =  x n /
x n /  yn = b/c, где с≠0.
yn = b/c, где с≠0.
Нахождение пределов последовательности:
Найти предел последовательности при n
а 8. Постоянный множитель можно выносить за знак предела:
 kxn =k
kxn =k xn
xn
а) хn = 1/n2
б) хn =2/n+5/n2+3
в)  2n2+3/ n2+4
2n2+3/ n2+4
Решение:
а) применив п правило «предел произведения», получим:
 ( 1/n
( 1/n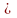 1/n) =
1/n) = 1/n
1/n 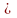
 1/n =0
1/n =0 =0
b) применим правило «предел суммы» и получим:
 ( 1/n-5/n2+3) =
( 1/n-5/n2+3) = 1/n-
1/n- 5/n2-lim3 = 0-0+3=3/
5/n2-lim3 = 0-0+3=3/
в) в подобных случаях применяют искусственный прием: делят числитель и знаменатель дроби почленно на наивысшую из имеющихся степень переменной n.
В данном примере разделим числитель и знаменатель дроби почленно на n2 . Имеем:
 ( 2n2+3/n2+4) =
( 2n2+3/n2+4) =  2n2+3/
2n2+3/  n2+4 =(
n2+4 =( 2n2/n2+
2n2/n2+ /n2) / (
 n2/n2 +
n2/n2 + 4/n2 ) =
4/n2 ) = =
=
=2. (здесь мы применили правило «предел дроби»).
Тест «Предел числовой последовательности»
1. Запиши окрестность точки а радиуса r в виде интервала, если а=8,r=0,3 Ответ: (2балла)
2. Вычисли  xn, если хn=4
xn, если хn=4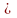 7n
7n
Ответ:  (4
(4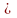 7n)= (2балла)
7n)= (2балла)
3.Вычисли
 ( 2n2+3/n2+4)=
( 2n2+3/n2+4)=
Ответ: (2балла)
4. Укажи каким будет номер n того члена последовательности (xn), начиная с которого все члены последовательности находятся в окрестности точки радиуса r. Хn=1/5n, а=0,r=0,1.
Ответ: n= (1балл)
5. Найди номер n0, начиная с которого все члены последовательности (xn) попадут в окрестность точки а=0 и радиус r=0,1, если Хn=-2/n и r=0,1
Ответ: (1 балл)
6. Вычисли:  6+ 7n2+4n/n2=
6+ 7n2+4n/n2=
Ответ: (3балла)
7.Найти предел последовательности  (n2+5 n) (3-n)+n3/n2+7=
(n2+5 n) (3-n)+n3/n2+7=
Ответ: (3балла)
8. Определи, каким будет предел последовательности: 7/2,14/3,21/4,28/5…7n/n+1… Ответ: (2балла)
9. Используя теорему Вейершрасса, докажи, имеет ли последовательность (xn) предел: xn(9n2+6)/n2
В доказательстве используй следующий план:
1. Исследуй последовательность на монотонность
а) является возрастающей и монотонной
б) является монотонной и убывающей
в) не является монотонной.
2.Исследуй последовательность на ограниченность.
Заданная последовательность:
а) является ограниченной
б)не является ограниченной
в)является ограниченной сверху
г)является ограниченной снизу
3. В выводах используй теорему Вейершрасса:
а)Если последовательность монотонна, то она имеет предел
б)Если последовательность имеет предел, то она монотонна
в) если последовательность не монотонна, то она не имеет предела
г)если последовательность монотонна и ограниченна, то она сходится
д)если последовательность ограничена, то она имеет предел
4. Выясни, имеет ли заданная последовательность предел:
А) не имеет предела
Б) имеет предел
5. Вычисли предел последовательности xn=
Ответ: 1.-------------, 2.----------------,3--------------- 4-------------, 5.---(6 баллов)

 Получите свидетельство
Получите свидетельство Вход
Вход












 Числовые последовательности. Способы задания и свойства числовых последовательностей (192.2 KB)
Числовые последовательности. Способы задания и свойства числовых последовательностей (192.2 KB)
 0
0 5133
5133 65
65 Нравится
0
Нравится
0


