Числовые множества

Презентация по математике

в 6 классе на тему «Множества»

Что такое множество?

Множество – это количество предметов или чисел, обладающих общими свойствами.

Данное определение подходит к любой совокупности с одинаковыми признаками, независимо оттого, сколько предметов в нее входит:

толпа людей, стог сена, звезды в небе.

В математике изучаемое понятие обозначается заглавными латинскими буквами, например: А, С, Z, N, Q, A1, A2 и т. д.

Объекты, составляющие группу, называются элементами множества и записываются строчными латинскими буквами: a, b, c, d, x, y, a 1 , a 2 и т. д.

Границы совокупности обозначаются фигурными скобками { }.

Пример : А = {а, в, с, у} – А состоит из четырех элементов. Записать совокупность Z согласных букв в слове «калькулятор»:

Z = {к, л, т, р}, повторяющиеся согласные записываются один раз. Z состоит из четырех элементов.

Принадлежность элементов множеству обозначается знаком – Є.

Пример : В = {в, а, н, я},

а Є В – элемент «а» принадлежит В.

Не принадлежит множеству обозначается знаком –  ∉

Пустое множество- ∅

Выделяют три вида множеств:

• конечные - совокупности, имеющие максимальный и минимальный предел (например, отрезок);

2) бесконечные - не являющиеся конечными (например, числовые);

3) пустые (обозначаются Ø) – не имеющие элементов.

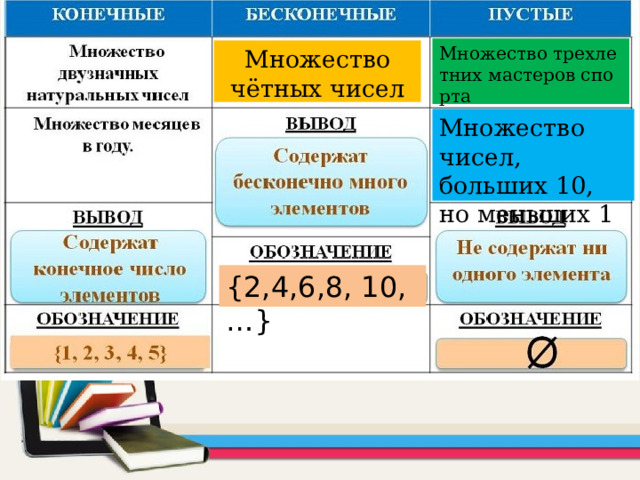
Множество трехлетних мастеров спорта

Множество чётных чисел

Множество чисел, больших 10, но меньших 1

{2,4,6,8, 10,…}

Подмножество  — это множество, все элементы которого, являются частью другого множества.

Рассмотрим два множества:

L = {учащиеся 6 класса}   и   M = {учащиеся школы}.

Каждый элемент множества  L  принадлежит и множеству  M,  значит, множество  L  является подмножеством множества  M.  Такое соотношение множеств обозначают знаком  ⊂: L⊂M. Запись  L⊂M  читается так:  множество  L  является подмножеством множества  M.

Если множества состоят из одинаковых элементов, их называют равными.

Пример:

А = {23, 29, 48} и В = {23, 29, 48}, тогда А = В.

Множество натуральных чисел

К совокупности натуральных чисел (N) относятся цифры, используемые при счете - от 1 до бесконечности.

Множество целых чисел

Совокупность целых чисел (Z) включает в себя положительные натуральные и отрицательные числа, а также ноль: Z = {-112, -60, -25, 0,58,256}. Следовательно, N - подмножество Z, что можно записать как N ⊆ Z. Любое натуральное число можно назвать так же и целым.

Множество рациональных чисел

Совокупность рациональных чисел (Q) состоит из дробей (обыкновенных и десятичных), целых и смешанных чисел: Q={-½; 0; ½, 5; 10}.

Любое рациональное число можно представить в виде дроби, у которой числителем служит любое целое число, а знаменателем – натуральное: 5 = 5/1 = 10/2 = 25/5; 0,45 = 45/100 = 9/20.

Следовательно, N и Z являются подмножествами Q.