Буквенная запись свойств действий над числами

ВВЕДЕНИЕ В АЛГЕБРУ

Буквенная запись свойств действий

над числами

Домашнее задание с.73-74 – читать; № 231(а), 237(а,б), 238(а, б).

Метапредмет – Знак

Выполняем тест (готовимся к ОГЭ)

Проверка полученных результатов. Коррекция

Выполняем тест (готовимся к ОГЭ)

Проверка полученных результатов. Коррекция

Выполняем тест (готовимся к ОГЭ)

Проверка полученных результатов. Коррекция

Цель нашего урока

Алгебра возникла и развивалась в недрах арифметики. Арифметика

учит обращаться с числами и с числовыми (арифметическими)

выражениями, алгебра - с буквами и буквенными (алгебраическими)

выражениями.

Переход от риторической алгебры к символической, в результате которого словесные правила были заменены формулами, а буквенные выражения сами стали предметом исчисления, происходил на протяжении нескольких веков.

Решительный шаг в этом направлении был сделан только в конце XVI в. французским математиком Франсуа Виетом, который ввёл в алгебру современные символы. Это стало настоящим прорывом, и сегодня уже невозможно представить математику без букв, символов, формул.

целеполагание

Для чего нужны буквы…

Арифметика — наука о числах, основные её задачи связаны

с вычислением значений числовых выражений. Но для того чтобы формулировать утверждения, которые составляют основу вычислительных приёмов, коротко и наглядно записывать свойства арифметических действий, нужны буквы.

Вхождение в тему урока и создание условий для осознанного восприятия нового материала.

Основные свойства

Работа с учебником

Стр. 73

!

!

Организация и самоорганизация учащихся. Организация обратной связи

Основные свойства

Работа с учебником

Стр. 74

!

Организация и самоорганизация учащихся. Организация обратной связи

От чисел к буквам

Независимо от того, какие конкретные числа берутся, мы пользуемся одним и тем же приёмом: чтобы вычесть из некоторого числа сумму двух чисел, вычитаем из него первое слагаемое и из полученного результата вычитаем второе слагаемое.

Организация и самоорганизация учащихся. Организация обратной связи

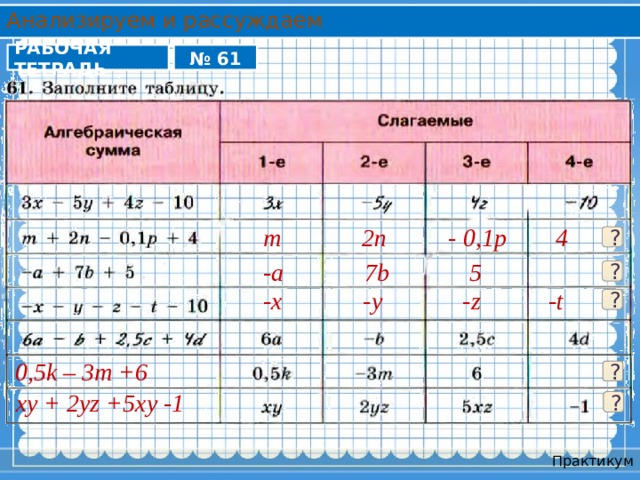
Анализируем и рассуждаем

РАБОЧАЯ ТЕТРАДЬ

№ 61

m 2n - 0,1p 4

?

-a 7b 5

?

-x -y -z -t

?

0,5k – 3m +6

?

xy + 2yz +5xy -1

?

Практикум

Анализируем и рассуждаем

РАБОЧАЯ ТЕТРАДЬ

№ 63

-b

?

-a

?

-3a + b

?

Практикум

Анализируем и рассуждаем

РАБОЧАЯ ТЕТРАДЬ

№ 64

4

?

2 -

?

- 3 - +

?

1 +2 - 3

?

Практикум

Рассуждаем

УЧЕБНИК

№ 229

256 + (100 – 2) = 256 + 100 – 2

87 – (50 – 1) = 87 – 50 + 1

?

?

Практикум

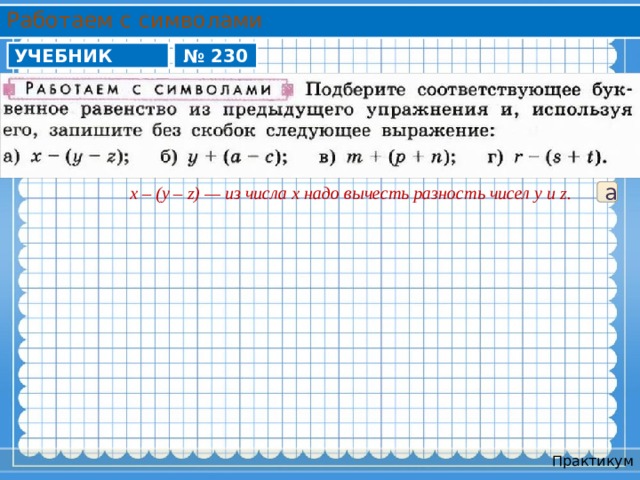
Работаем с символами

УЧЕБНИК

№ 230

x – (y – z) — из числа x надо вычесть разность чисел y и z.

а

Практикум

Работаем с символами

УЧЕБНИК

№ 232

Всего продали a + b + c пакетов, в каждом из них x г орехов, поэтому общая масса орехов

(в граммах) равна x(a + b + c).

Способ 1

Масса пакетов (в граммах) с грецкими орехами равна xa, с арахисом — xb, с фундуком — xc, поэтому их общая масса равна xa + xb + xc.

Имеем равенство: x(a + b + c) = xa + xb + xc.

Способ 2

Практикум

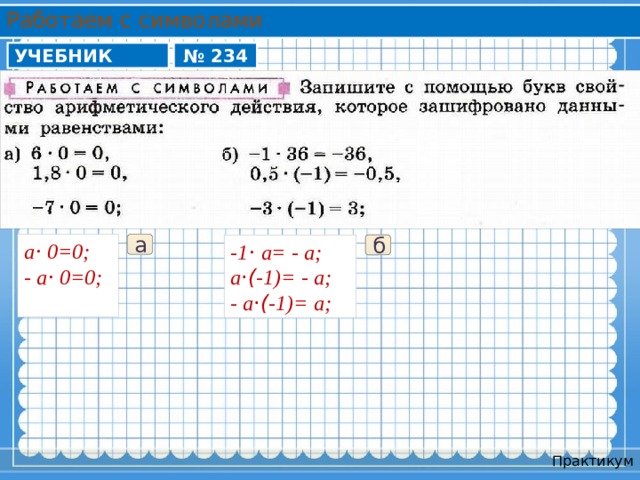
Работаем с символами

УЧЕБНИК

№ 234

а ⋅ 0=0;

а

- а⋅ 0=0;

б

-1 ⋅ а= - а;

а ⋅( -1)= - а;

- а ⋅( -1)= а;

Практикум

Работаем с символами

УЧЕБНИК

№ 237

а

б

Практикум

Работаем с символами

УЧЕБНИК

№ 240

?

Практикум

Отрабатываем алгоритм

Дидактические материалы

С.33

Образец

Практикум

Отрабатываем алгоритм

Дидактические материалы

С.33-34

Практикум

Отрабатываем алгоритм

Дидактические материалы

С.33-34

Практикум

Самостоятельная работа

Дидактические материалы

С.119

Проверка полученных результатов. Коррекция

Вопросы и задания

• Назовите и запишите в буквенном виде основные свойства сложения и умножения чисел.
• Какие вычислительные приёмы рассмотрены в примерах 1 и 2? Назовите их и запишите соответствующие равенства с помощью букв.
• Два вычислительных приёма записаны в буквенном виде: a + (b – c) = a + b – c; (a – b)c = ac – bc. Назовите и сформулируйте каждый из них; приведите иллюстрирующие их числовые примеры.

Подведение итогов, рефлексия,  домашнее задание.

Магический квадрат

Какие выражения мы можем составить

с помощью магического квадрата?

6

а

b

2

5

7

4

1

8

14

Подведение итогов, рефлексия,  домашнее задание.