Арифметическая прогрессия

Урок в 9-м классе по теме «Арифметическая прогрессия»

Тип урока: урок обобщения и систематизации знаний.

Цель урока: усвоение знаний в их системе, умение самостоятельно применять полученные ЗУН, осуществлять их перенос в новые условия. 
Задачи:

• образовательные: повторить теоретический материал; вырабатывать навык решения задач с использованием формул суммы n первых членов арифметической прогрессии; решить большое количество заданий по теме; отработать навыки решения логических задач; подготовить учащихся контрольной работе;

• воспитательные: воспитание целеустремленности, организованности, ответственности, самостоятельности, умение общаться; 

• развивающие: развитие математической логики, самостоятельности, речи, внимания и кругозора, познавательного интереса к предмету.

Оборудование: демонстрационный ПК (или мультимедиа проектор и экран), слайды в презентации к уроку, карточки для самостоятельной работы.
Подготовка к уроку: учитель готовит презентацию к уроку, зашифрованное изречение, подбирает логические задания по теме: 19 основных заданий и 8 штрафных.
План урока

1. Организационный момент, историческая справка. 

2. Устный счет, проверка домашнего задания. 

3. Проверочная работа. 

4. Подготовка к контрольной работе в игровой форме.

5. Итог урока, домашнее задание.

Ход урока

1. Организационный момент, историческая справка

«Помните, что решая маленькие задачи, вы готовитесь к решению больших и трудных».

Рассказать предание о маленьком Карле Гауссе, будущем не­мецком короле математики, решившем в десятилетнем возрасте очень быстро задачу о нахождении суммы первых ста натуральных чисел. 

2. Устный счет, проверка домашнего задания (Демонстрация решения отдельных учащихся, записанных на доске в ходе устного счета.)
Задания устного счёта
1) Игровой момент. Учитель. Я задумал некоторую арифметическую прогрессию. Задайте только два вопроса и сразу назовите, чему равна S₁₀₀. 
2) Задайте арифметическую прогрессию с помощью всего двух чисел, причем нельзя использовать а₁ и d. [3]

1. Из предложенных последовательностей выберите ту, которая является арифметической прогрессией

а) 2; 4; 8; 16 б) -7; -7; -7; -7 в) 1; 3; 9; 27

2. Какая из данных арифметических прогрессий является возрастающей?

а) 15; 12; 9; 6 б) 3; 3; 3; 3 в) 5; 8; 11; 14

3. Найдите а₅, если а₁=-7, d =3 .

а) 5 б) 13 в) -21

4. Найдите a₁ , если a₄=18, d=-3 .

а) 54 б) 27 в)9

5.Известно, что a₁=-2, d=3, a_n =118. Найдите n.

а) 41 б) -23 в) 23

6. Известно, что a₁=7, a₁₅=-35. Найдите d.

а) -3 б) 3 в) 2
3. Проверочная работа (в 2-х вариантах) [1]. 
Каждый учащийся выполняет работу самостоятельно, и обязан оформить в тетради три задания полностью.
I вариант
1) Найдите номер члена последовательности (a_n), равного 150, если эта последовательность задана формулой a_n=6n+18.
Ответ: n =_______ 
2) Заполните пропуски в формулировке определений, свойств и в истинных утверждениях.
а) Разность арифметической прогрессии можно найти по формуле: d=a_n+1 - ____.
б) Формула n-го члена арифметической прогрессии такова: a_n=____ + d(____). 
в) Сумму п первых членов арифметической прогрессии можно найти по формуле:

3) Выпишите три следующих члена последовательности (у_n) : 1; 3; … если известно, что она является арифметической прогрессией. Найдите 47-й член этой прогрессии. Подчеркните верный из предложенных ответов.
Ответы:
_______________________________ а) 93;
_______________________________ б) 100;
_______________________________ в) 95.
4) Найдите сумму 10-ти первых членов арифметической прогрессии (x_n), если x₁=12; d=-2. Из предлагаемых ответов подчеркните верный ответ.
Ответы:
_____________________________________________________ a) S₁₀ = 210;
_____________________________________________________ б) S₁₀ = 30;
_____________________________________________________ в) S₁₀ = 60. 

II вариант
1) Последовательность задана формулой y_n=11-3n. Найдите: а) у₁₀; б) у_к-1 
Ответы: у₁₀=____; у_к-1=_____.
2) Заполните пропуски в формулировке определений, свойств и в истинных утверждениях.
а) Арифметической прогрессией называется последовательность, каждый член которой, начиная со второго, равен _______________________ , сложенному с ________________ числом.
б) Число d называется____________________ арифметической прогрессии.
в) Сумму n первых членов арифметической прогрессии можно найти по формуле

3) Арифметическая прогрессия (a_n) задана двумя первыми числами 10; 4; ... Выпишите три следующих числа и найдите a₁₁. Подчеркните верный из предложенных ответов в нахождении a₁₁. 
Ответы:
_____________________________________________________ а) 70;
_____________________________________________________ б) -50;
_____________________________________________________ в) -56.
4) Найдите сумму первых двадцати членов арифметической прогрессии (c_n), если c₁=2; d=3. Из предлагаемых ответов подчеркните верный.
Ответы: 
______________________________________________________ a) S₂₀ = 600;
______________________________________________________ б) S₂₀ = 610;
______________________________________________________ в) S₂₀ = 480.
(Взаимопроверка после выполнения путём сравнения с правильными ответами) 

Найдите сумму двенадцати первых членов арифметической прогрессии, если а d

а) 294 б) 41 в) 57

2. Известно, что a n S₈ . Найдите d.

а) 5 б) 3 в) 9

3. Найдите сумму первых четырнадцати членов арифметической прогрессии, заданной формулой a_n =5n-1 .

а) 497 б) 511 в)1022
4. Подготовка к контрольной работе в игровой форме 
Класс делится на две команды. [2] 
Условие игры. В этом изречении 19 различных букв. Команды по очереди называют буквы, если такая буква есть, то учащийся этой команды, назвавший букву, получает задание, решив которое, можно открыть букву; если названная буква отсутствует, то он получает штрафное задание. Учащийся, получивший задание приступает к его выполнению. Остальные члены команды продолжают называть буквы, пока все не получат свое задание. (Приложение )

Зашифрованное изречение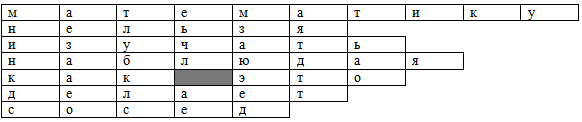



Побеждает та команда, которая открыла больше букв и прочитала расшифрованное изречение. 
Автором зашифрованного изречения является профессор математики, писатель фантастических повестей Ларри Нивен. 
5. Итог урока
В конце работы выявляются причины ошибок или затруднений. Учащиеся оценивают свое участие в работе команды.

• Что нового вы узнали на уроке? 

• Достигли ли вы, поставленной в начале урока, цели? 

• Какую цель вы для себя ставите на следующем уроке? 

6. Домашнее задание §7; решить 379; № 383; 384.