Анализ ЕГЭ по математике 2013 года

Работа предназначена для учителей математики и учащихся выпускных классов. В презентации предлагается пошаговое решение всех задач части В и четырех заданий части С. К каждому  номеру предлагается ответ и показано как правильно его записать в бланк ответов на экзамене. Возможно использование на уроке, на факультативном занятии, при самостоятельной подготовке к ЕГЭ.

Задание В 1

 Одна таблетка лекарства весит 70 мг и содержит 4% активного вещества. Ребёнку в возрасте до 6 месяцев врач прописал 1,05 мг активного вещества на каждый килограмм веса в сутки. Сколько таблеток этого лекарства следует дать ребёнку в возрасте 5 месяцев и весом 8 кг в течении суток.

Решение - смотрите презентацию

Задание В 2

На диаграмме показано распределение выплавки меди в 10 странах за 2006г. Среди представленных стран первое место у США, десятое у Казахстана. Какое место у Канады?

Презентация содержит 41 слайд с заданиями и решениями.

Анализ ЕГЭ по математике 2013 года

Рыбалко И.В.

Учитель математики МБОУ

Лицей № 11 г. Ульяновск

Задание В 1

Одна таблетка лекарства весит 70 мг и содержит 4% активного вещества. Ребёнку в возрасте до 6 месяцев врач прописал 1,05 мг активного вещества на каждый килограмм веса в сутки. Сколько таблеток этого лекарства следует дать ребёнку в возрасте 5 месяцев и весом 8 кг в течении суток.

Задание В 1 (решение)

3

В 1

х

3

х

1

0

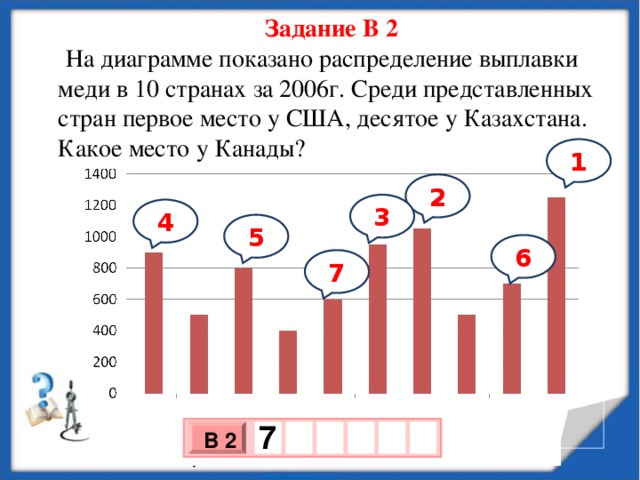
Задание В 2

На диаграмме показано распределение выплавки меди в 10 странах за 2006г. Среди представленных стран первое место у США, десятое у Казахстана. Какое место у Канады?

1

2

3

4

5

6

7

7

В 2

х

3

х

1

0

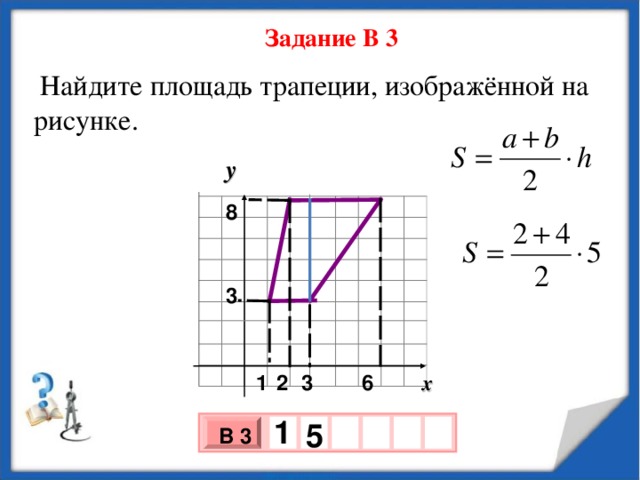
Задание В 3

Найдите площадь трапеции, изображённой на рисунке.

y

8

3

1

6

x

2

3

1

5

В 3

х

3

х

1

0

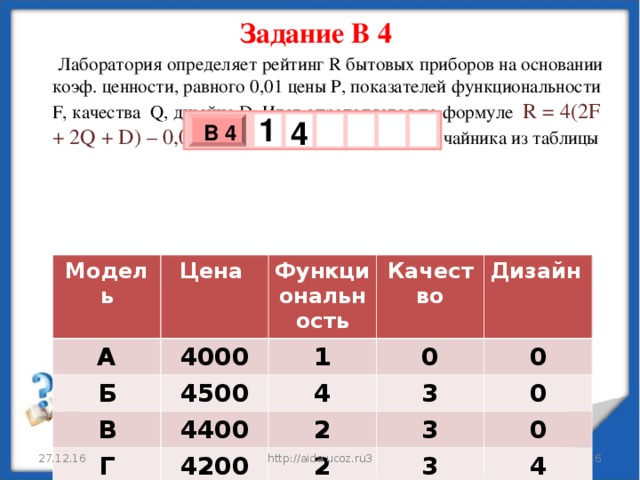
Задание В 4

Лаборатория определяет рейтинг R бытовых приборов на основании коэф. ценности, равного 0,01 цены Р, показателей функциональности F, качества Q, дизайна D . Итог определяется по формуле R = 4(2F + 2Q + D) – 0,01P . Определи высший рейтинг чайника из таблицы

1

4

В 4

х

3

х

1

0

Модель

А

Цена

Б

Функциональность

4000

В

Качество

1

4500

0

4400

4

Дизайн

Г

0

3

2

4200

0

3

2

0

3

4

27.12.16

http://aida.ucoz.ru 3

Задание В 5

Найдите корень уравнения

8

В 5

х

3

х

1

0

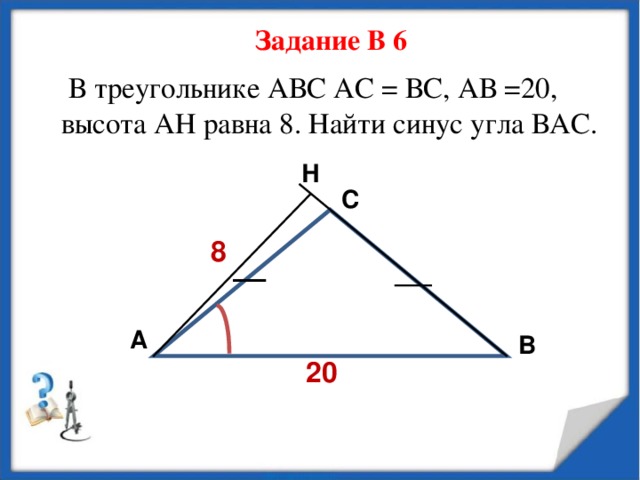
Задание В 6

В треугольнике АВС АС = ВС, АВ =20, высота АН равна 8. Найти синус угла ВАС.

Н

С

8

А

В

20

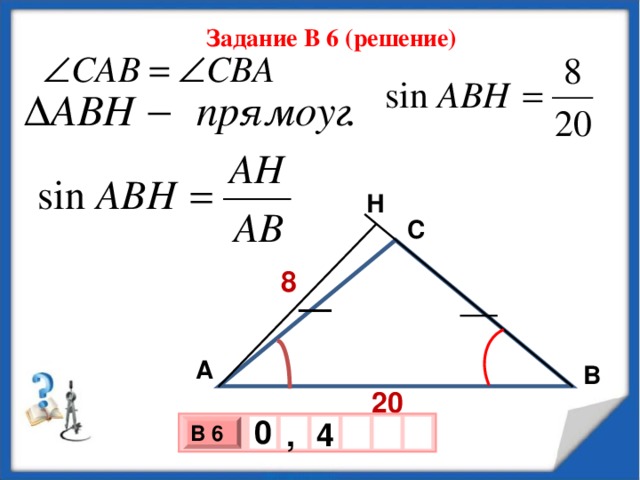
Задание В 6 (решение)

Н

С

8

А

В

20

0

4

,

В 6

х

3

х

1

0

Задание В 7

Найдите значение выражения

6

В 7

х

3

х

1

0

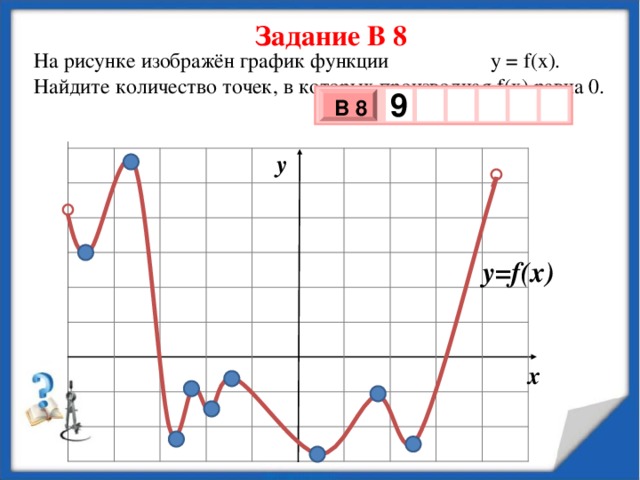
Задание В 8

На рисунке изображён график функции у = f( х ) . Найдите количество точек, в которых производная f( х) равна 0.

9

В 8

х

3

х

1

0

у

у= f(x)

х

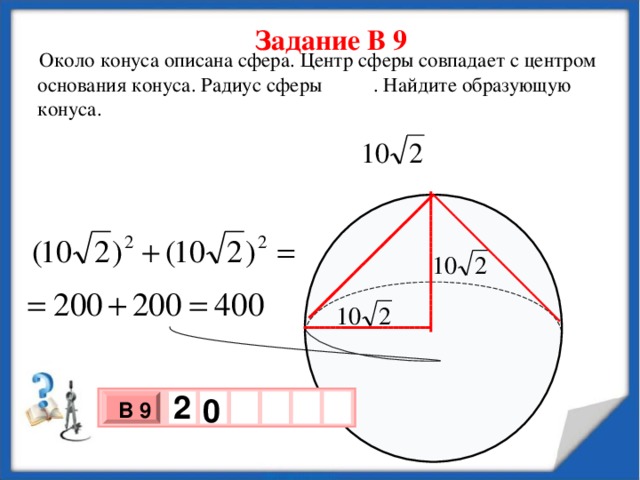
Задание В 9

Около конуса описана сфера. Центр сферы совпадает с центром основания конуса. Радиус сферы . Найдите образующую конуса.

2

0

В 9

х

3

х

1

0

Задание В 10

Перед началом турнира по теннису участников разбивают на игровые пары случайным образом. Всего участников 76, среди них 7 спортсменов из России, в том числе Анатолий Москвин. Найти вероятность того, что в первом туре Москвин будет играть с теннисистом из России.

Задание В 10 (решение)

0

0

,

8

В 10

х

3

х

1

0

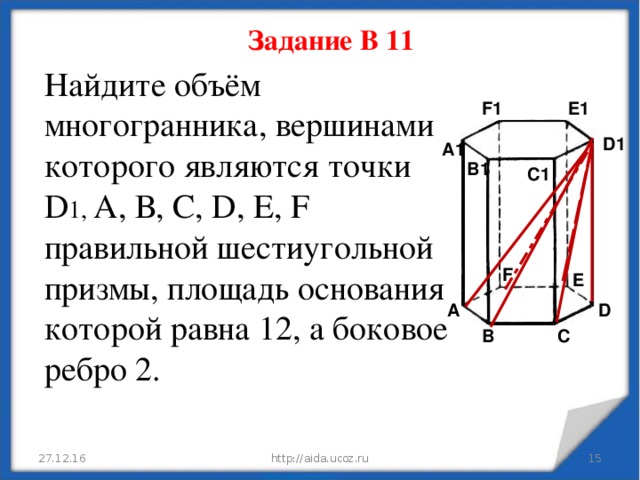
Задание В 11

Найдите объём многогранника, вершинами которого являются точки D 1 , А, В, С, D, E, F правильной шестиугольной призмы, площадь основания которой равна 12, а боковое ребро 2.

F1

E1

D1

A1

B1

C1

F

E

D

A

C

B

14

http://aida.ucoz.ru

27.12.16

15

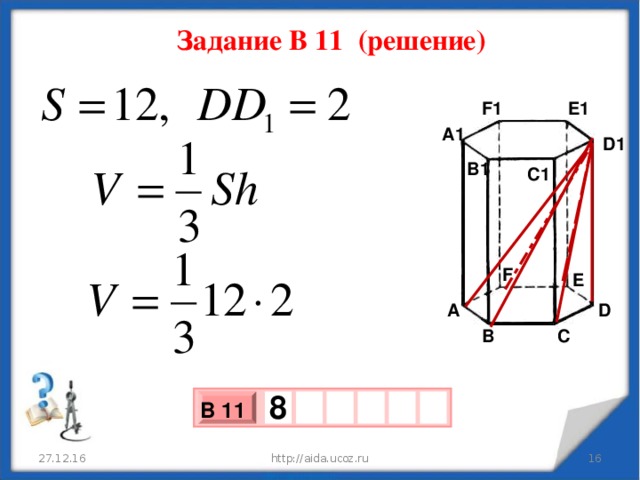
Задание В 11 (решение)

F1

E1

A1

D1

B1

C1

F

E

D

A

C

B

8

В 11

х

3

х

1

0

27.12.16

http://aida.ucoz.ru

15

16

Задание В 12

Локатор батискафа, равномерно погружающегося вертикально вниз, испускает импульсы частотой 217 МГц. Скорость погружения, выражаемая в м/с, определяется по формуле

где с=1500 м\с –скорость звука в воде,

f 0 – частота испускаемых импульсов (в МГц), f - частота отражённого от дна сигнала, регистрируемая приёмником. Определите наибольшую возможную частоту отражённого сигнала f , если скорость погружения батискафа не должна превышать 12 м\с. Ответ выразите в МГц .

Задание В 12 (решение)

Дано: Решение:

f 0 = 217 МГц.

с = 1500 м\с

v ≤ 12 м\с

Найти:

f - ?

0

5

,

2

2

В 12

х

3

х

1

0

Задание В 13

Байдарка в 10:00 вышла из пункта А в пункт В, расположенный от А в 15 км. Пробыв в пункте В 1 час 20 мин, байдарка отправилась обратно и вернулась в пункт А в 16:00 того же дня. Определить (в км\ч) собственную скорость байдарки, если известно, что скорость течения реки равна 2 км/ч.

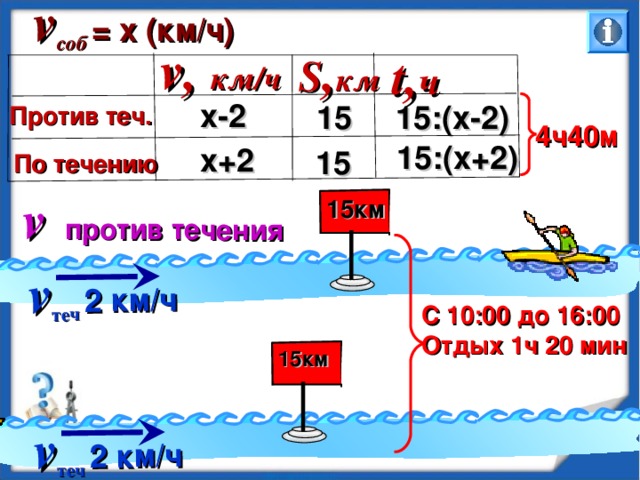
v соб = х (км/ч)

v

против течения

v теч 2 км/ч

v теч 2 км/ч

v, км/ч

S , км

t , ч

х-2

15:(х-2)

15

Против теч.

4ч40м

15:(х+2)

х+2

15

По течению

15км

С 10:00 до 16:00

Отдых 1ч 20 мин

15км

20

Задание В 13 (решение)

7

В 9

х

3

х

1

0

Задание В 14

Найдите наименьшее значение функции

на отрезке .

Решение:

Задание В 14 (решение)

Найдите наименьшее значение функции

на отрезке .

4

2

В 9

х

3

х

1

0

Задание С 1

а) Решите уравнение .

б) Найдите все корни уравнения, принадлежащие отрезку

Задание С 1

а) Решите уравнение .

Решение:

Задание С 1

б) Найдите все корни уравнения, принадлежащие отрезку

Задание С 2

В правильной четырёхугольной пирамиде МАВС D с вершиной М стороны основания равны 6, а боковые рёбра равны 12. Найдите площадь сечения пирамиды плоскостью, проходящей через точку С, середину ребра МА и параллельно прямой В D .

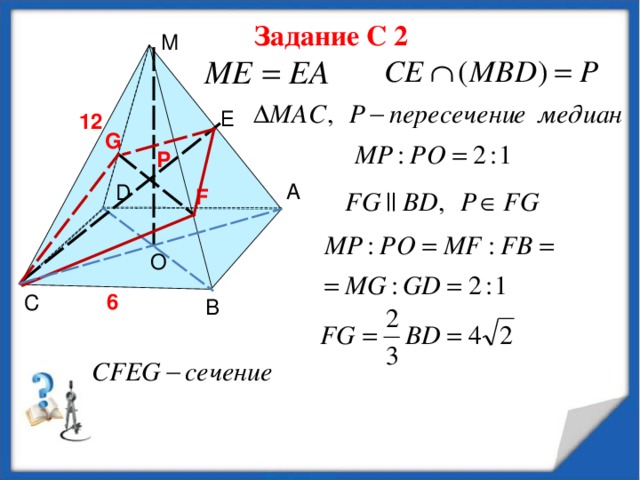
F

Задание С 2

М

Е

12

G

Р

А

D

О

6

С

В

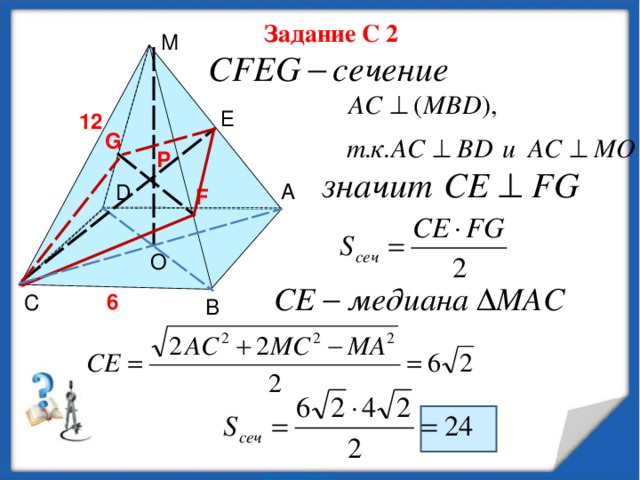
F

Задание С 2

М

Е

12

G

Р

А

D

О

6

С

В

Задание С 3

Решите систему неравенств

Решим первое неравенство:

Задание С 3

Нет решений

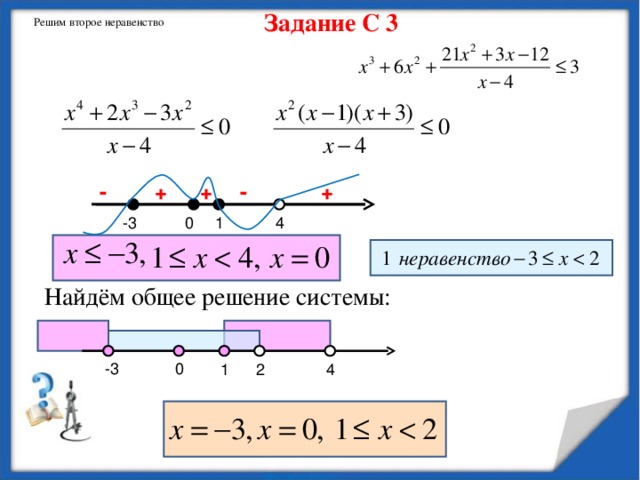
Решим второе неравенство

Задание С 3

-

+

+

+

-

4

1

0

-3

Найдём общее решение системы:

0

-3

4

2

1

Задание С 4

Окружности радиусов 2 и 3 с центрами О 1 и О 2 соответственно касаются в точке А. Прямая, проходящая через точку А, вторично пересекает меньшую окружность в точке В, а большую – в точке С. Найдите площадь треугольника ВСО 2 , если

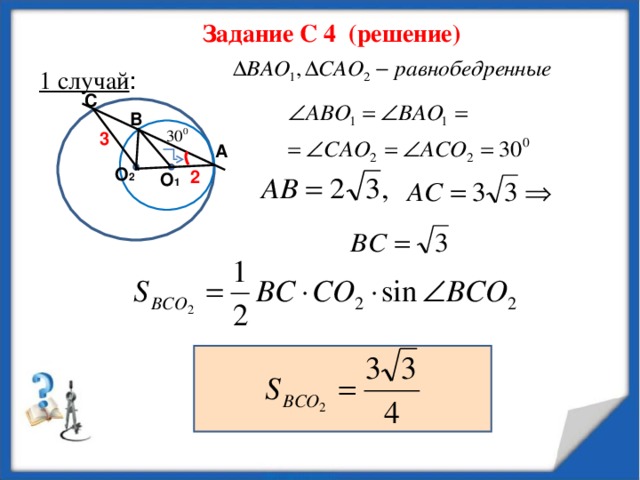
Задание С 4 (решение)

1 случай :

С

В

3

A

О 2

2

О 1

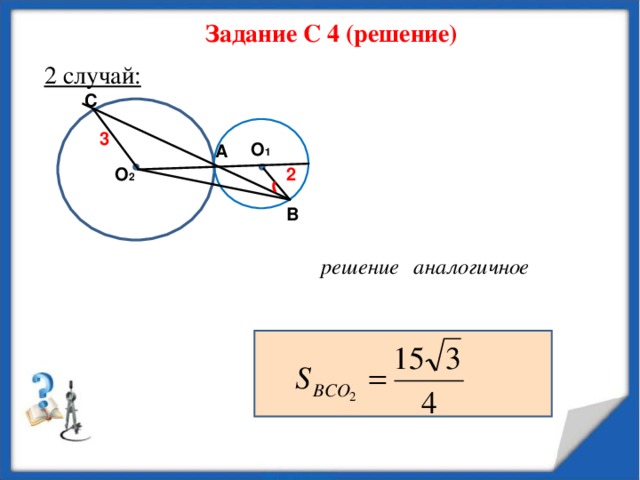
Задание С 4 (решение)

2 случай:

С

3

О 1

A

О 2

2

В

Задание С 5

Найдите все значения а, при каждом из которых уравнение

имеет единственный корень.

Задание С 6

Задумано несколько (не обязательно разных) натуральных чисел. Эти числа и их возможные суммы (по 2, по 3 и т.д.) выписывают на доску в порядке не убывания. Если какое-то число n , выписанное на доску, повторяется несколько раз, то на доске остаётся одно такое число n , а остальные числа равные n стираются. Например, если задуманы числа 1, 3, 3,4, то на доске будет набор 1, 3, 4, 5, 6, 7, 8, 10, 11.

А) Приведите пример задуманных чисел, для которых на доске будет записан набор 2, 4, 6, 8.

Задание С 6

Задумано несколько (не обязательно разных) натуральных чисел. Эти числа и их возможные суммы (по 2, по 3 и т.д.) выписывают на доску в порядке не убывания. Если какое-то число n , выписанное на доску, повторяется несколько раз, то на доске остаётся одно такое число n , а остальные числа равные n стираются. Например, если задуманы числа 1, 3, 3,4, то на доске будет набор 1, 3, 4, 5, 6, 7, 8, 10, 11.

Б) Существует ли пример таких задуманных чисел, для которых на доске будет записан набор 1, 3, 4, 5, 6, 9, 10, 11, 12, 13, 14, 17, 18, 19, 20, 22.

Задание С 6

Задумано несколько (не обязательно разных) натуральных чисел. Эти числа и их возможные суммы (по 2, по 3 и т.д.) выписывают на доску в порядке не убывания. Если какое-то число n , выписанное на доску, повторяется несколько раз, то на доске остаётся одно такое число n , а остальные числа равные n стираются. Например, если задуманы числа 1, 3, 3,4, то на доске будет набор 1, 3, 4, 5, 6, 7, 8, 10, 11.

В) Приведите все примеры задуманных чисел, для которых на доске будет записан набор 9, 10, 11, 19, 20, 21, 22, 30, 31, 32, 33, 41, 42, 43, 52.

Удачи на экзаменах!

Ссылки

1. Материалы ЕГЭ по математике ФИПИ

2. Слайд с задачей В 13 - le-savchen.ucoz.ru/load/14-1-0-136

3. Картинка «Сдадим ЕГЭ на отлично» - http://dist-tutor.info/course/view.php?id=8

4. Шаблон для презентации - edu-teacherzv.ucoz.ru/load/shablony_i_fony_dlja_prezentacij/shablony_powerpoint_dlja_uchitelja_matematiki_chast_1/4-1-0-63

27.12.16

http://aida.ucoz.ru

23