Алгоритм решения дробных - рациональных неравенств

Алгоритм решения дробных - рациональных неравенств

()

1. Перенести все в одну сторону с противоположным знаком.

2. Разложить знаменатели на линейные множители или их степени.

3. Привести к общему знаменателю:

• разложить на множители в знаменатели дробей;

• под общей дробной чертой выписать множители первой дроби;

• приписать к нему недостающие множители второго, третьего,…знаменателя, одинаковые сомножители записать в виде степеней.

и записать его под общей дробной чертой.

4. Записать под каждой дробью дополнительные множители.

5. В числители общей дроби записать результаты умножения числителя каждой дроби на дополнительные множители, при этом используя:

• правила умножения одночлена на одночлен;

• правила умножения многочлена на многочлен

• правило раскрытия скобок.

6. В числители привести подобные и разложить его на множители.

Получим:

() 0

-дробное - рациональное неравенство вида I-III

I. Линейные неравенства и неравенства сводимые к ним (если осталась одна линейная скобка).

А

x-b()0,

(x-a)²≠0,

(x-c)²≠0,

(x-d)²≠0,

≠0,

(x-m)²≠0,

(x-k)²≠0;

лгоритм решения

П

Система!

1. Строгие неравенства:

()0

x ( b,

x≠a,

x≠c,

x,

x≠d,

x≠n,

x≠k.

a b c d e m n k x

­

a b c d e m n k x

Ответ: (b,c)(c,d)(d,e)

Ответ: (-∞,a) (a,b).

2

Объединение систем!

≥(≤)0

x-b≥(≤) 0,

e-x≥(≤)0,

(x-a)²≠0,

(x-k)²≠0,

(x-m)²≠0.

(x-a)²≠0,

X ≤ e,

X ≠ d,

X ≠ k,

X ≠ m.

Обл. определения

Обл. опр.

или

(x-c)²≠0

X ≤ e

X ≠ d

x≠ k

x ≠m

=0

X ≠d

X ≠k

X ≠m

Обл. опр.

и

Обл. опр.

или

Объединению систем!

X ≥(≤)b,

x≤e,

x≠d, или

x≠k,

x≠m.

x =a,

x≤e,

x≠d, или

x≠k,

x≠m.

x≠c,

x≤e, или

x≠d,

x≠k.

x≠m

x=e,

x≠d,

x≠k,

x≠m.

­­

­ ­­­­­­ ­­ x=a, т.к a∈ обл.опред.;x=c, т.к. c∈ обл.опред; x=e, т.к. e∈ обл.опред;

b d e m k x

Объединим полученные решения:

a b c d e x

Ответ: [b;d)(d;e], x=a.

b d e m k x

x≤b или x=a или x=c или x=e

Объединим полученные решения;

a b c d e x

Ответ: (-∞;b), x=c, x=e.

II. Квадратные неравенства и неравенства сводимые к ним (когда две линейные функции).

1). ax²+bx+c(0 a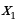(x- )(x-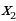 ) (0 (D0)

2). 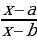(0 (x-a)(x-b) (0

3). 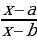≥(≤)0 ,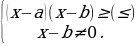

Неравенства вида 1)-3) решаем с помощью параболы (когда две линейные функции).

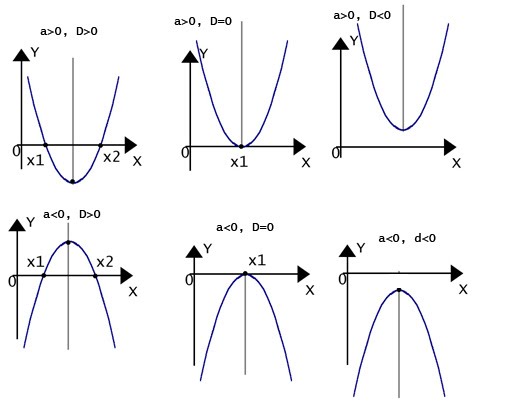
Решая неравенства вида 1) -3) изображаем одну из шести парабол.

Т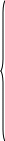 .о. в неравенствах I-II вида проводится пропедевтика решения неравенств методом интервалов.

(

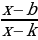(x-a)²≠0

(x-c)²≠0

0

(x-d)²≠0

(x-m)²≠0

(n-x)²≠0

()0

Обл. опред.

(x-b)(x-k)(

x≠a

x≠c

x

x≠d

x≠m

x≠n

+ - +

a b c d e m n k x

Ответ: (-∞;a) (a;b).

Ответ: (b;с) (с;d) (d;e).

≥(≤)0

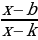
x≠a

x≤e

x≠d

x≠m

x≠n

X=c

x≤e

x≠d

x≠m

x≠n

x=e

x≠d

x≠m

x≠n

≥(≤)0

x

Обл. опред.

или

или

или

≤e

x≠m

x≠n

x≠d

X=e

x≠d

x≠m

x≠n

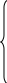
(x-b)(x-k)≥(≤)0

x≠k

x≤e

x≠m

x≠n

x≠d

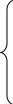
X=a

x≤e

x≠d

x≠m

x≠n

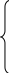
X=c

x≤e

x≠d

x≠m

x≠n

или

или

или

+ _ +

b d e m n k x

(-∞;b] или x=a или x=c или x=e.

[b;d)(d;e] или x=a или x=c или x=e.

Объединим полученные решения:

a b c e x

a b c d e x

Ответ: (-∞;b] , x=c, x=e.

Ответ: [b;d)(d;e) , x=a.

III. Неравенства высших степеней.

Метод интервалов (если остается линейных скобок больше или равно трем).

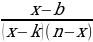()0

()0

x≠a

x≠c

x

x≠d

x≠m

_

+

_

+

a b c d e m n k x

О

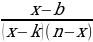≥(≤)0

e-x≥0 или

x≠d

x≠m

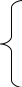
(x-a)²=0

x≤e

x≠d или

x≠m

твет: (-∞; a)(a;b).

Ответ: (b;c)(c;d)(d;e).

≥(≤)0

=0

x≠d

x≠m

(x-c)²=0

x≤e

x≠d или

x≠m

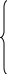
Ответ: (-∞;b], x=c, x=e.

Ответ: [b;d)(d;e], x=a.