Алгебра и начала анализа. Экстремумы функции.

Алгебра и начала анализа 11 класс

ГУО Средняя школа

№ 99 г. Минск

Экстремумы функции

Введение

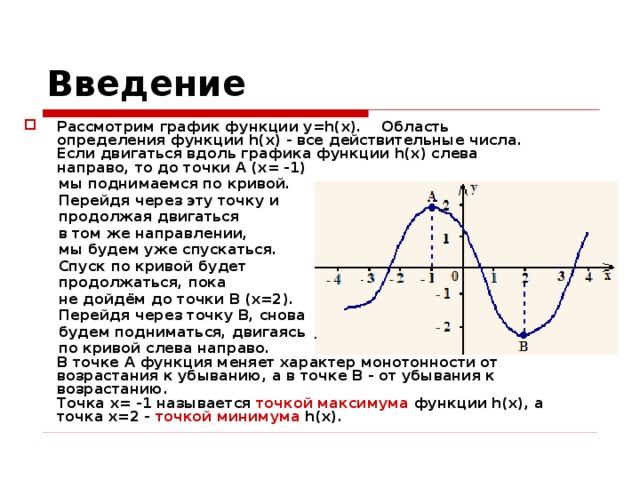
• Рассмотрим график функции y=h(x).  Область определения функции h(x) - все действительные числа. Если двигаться вдоль графика функции h(x) слева направо, то до точки A (x= -1)

мы поднимаемся по кривой.

Перейдя через эту точку и

продолжая двигаться

в том же направлении,

мы будем уже спускаться.

Спуск по кривой будет

продолжаться, пока

не дойдём до точки B (x=2).

Перейдя через точку B, снова

будем подниматься, двигаясь

по кривой слева направо. В точке A функция меняет характер монотонности от возрастания к убыванию, а в точке B - от убывания к возрастанию. Точка x= -1 называется точкой максимума функции h(x), а точка x=2 - точкой минимума h(x).

Окрестность точки

При исследовании поведения функции вблизи некоторой точки удобно пользоваться понятием окрестности.

• Определение Окрестностью точки а называется любой интервал, содержащий эту точку.

Например, интервал (2; 6) - одна из окрестностей точки 3, интервал (-3,3;-2,7) - окрестность точки -3.

Точка максимума

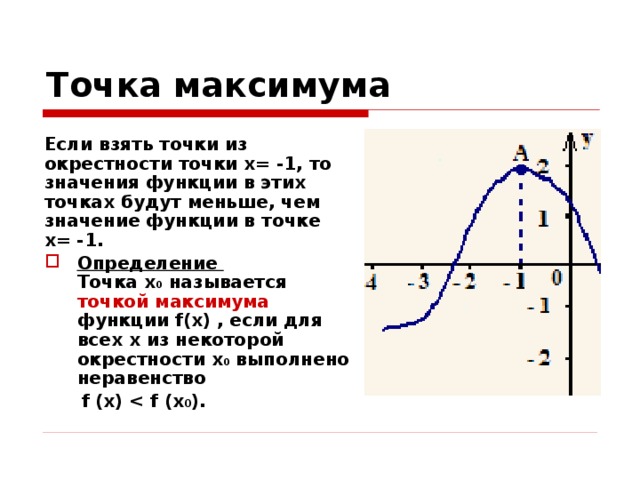
Если взять точки из окрестности точки x= -1, то значения функции в этих точках будут меньше, чем значение функции в точке x= -1.

• Определение Точка x 0 называется точкой максимума функции f(x) , если для всех x из некоторой окрестности x 0 выполнено неравенство

f (x) 0 ).

f (x 0 ). " width="640"

Точка минимума

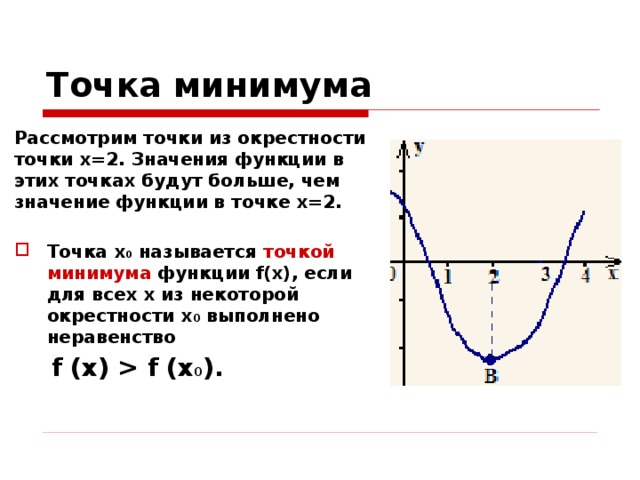
Рассмотрим точки из окрестности точки x=2. Значения функции в этих точках будут больше, чем значение функции в точке x=2.

• Точка x 0 называется точкой минимума функции f(x), если для всех x из некоторой окрестности x 0 выполнено неравенство

f (x) f (x 0 ).

Экстремумы функции

• Точки максимума и минимума называются точками экстремума функции и обозначаются:

x max ,  x min .

• Значения функции в этих точках называются экстремумами функции и обозначаются: y max = f(x max ),   y min = f(x min ).

КОНЕЦ