Аксиомы стереометрии.

10 класс геометрия

Аксиомы стереометрии

Учитель: Олейникова И.В.

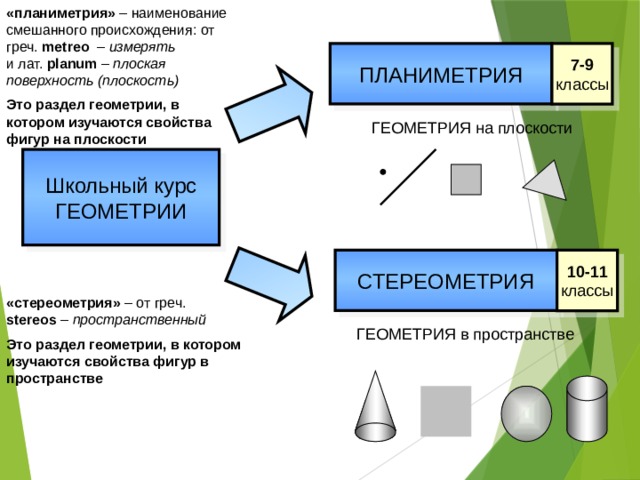
«планиметрия»  – наименование смешанного происхождения: от греч. metreo  – измерять и лат. planum  – плоская поверхность (плоскость)

Это раздел геометрии, в котором изучаются свойства фигур на плоскости

7-9 классы

ПЛАНИМЕТРИЯ

ГЕОМЕТРИЯ на плоскости

Школьный курс ГЕОМЕТРИИ

10-11 классы

СТЕРЕОМЕТРИЯ

«стереометрия»  – от греч. stereos  – пространственный

Это раздел геометрии, в котором изучаются свойства фигур в пространстве

ГЕОМЕТРИЯ в пространстве

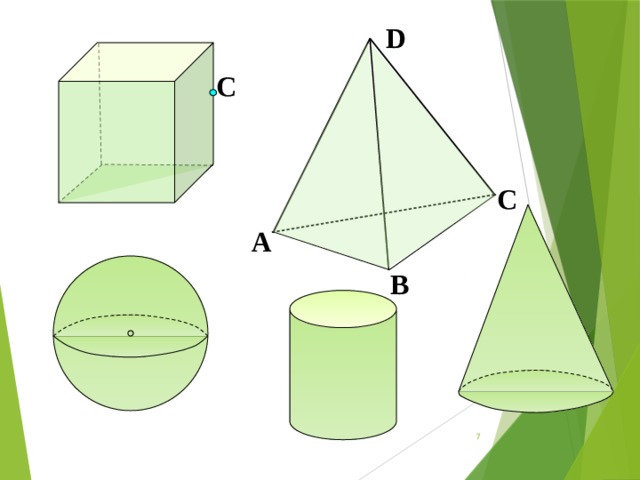
К

n

М

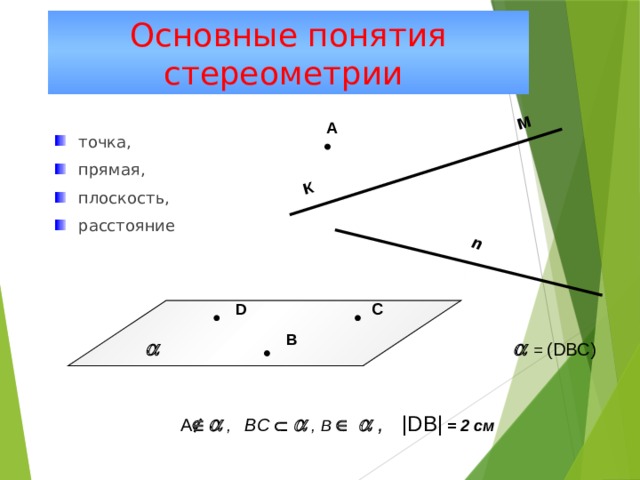
Основные понятия стереометрии

А

• точка,
• прямая,
• плоскость,
• расстояние

D

С

В

 = (DВС)



A   , ВC   , В   , |DВ| = 2 см

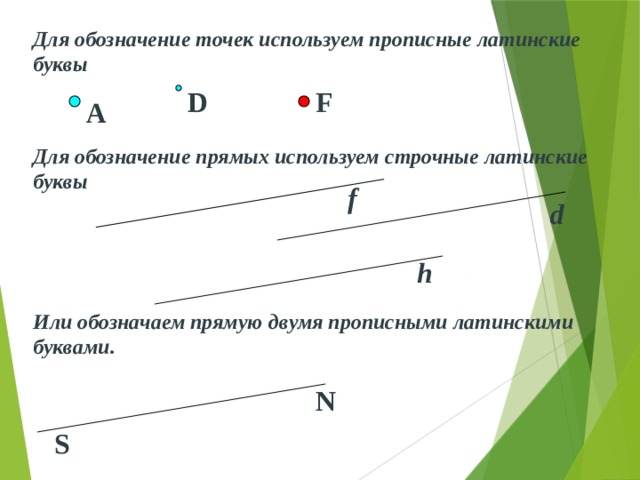
Для обозначение точек используем прописные латинские буквы

D

F

A

Для обозначение прямых используем строчные латинские буквы

f

d

h

Или обозначаем прямую двумя прописными латинскими буквами.

N

S

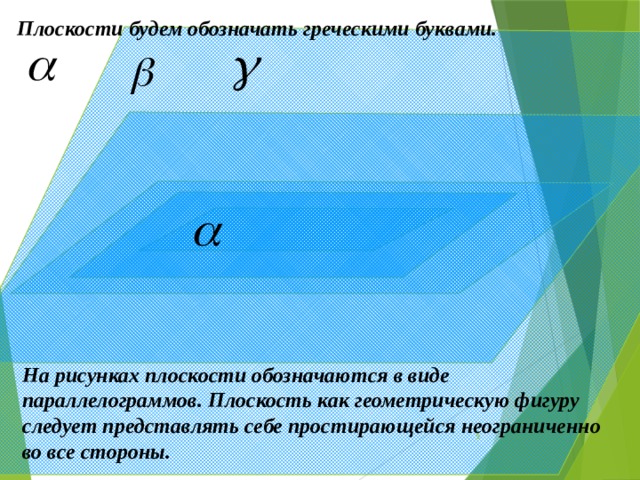
Плоскости будем обозначать греческими буквами.

На рисунках плоскости обозначаются в виде параллелограммов. Плоскость как геометрическую фигуру следует представлять себе простирающейся неограниченно во все стороны.

4

ОБОЗНАЧЕНИЯ

Точка A принадлежит прямой a

Точка B не принадлежит прямой a

Точка A принадлежит плоскости

Точка B не принадлежит плоскости

Прямая a лежит в плоскости

Прямая b не лежит в плоскости

Прямая b пересекает плоскость в точке A

Плоскости и пересекаются по прямой c

6

D

C

C

A

B

6

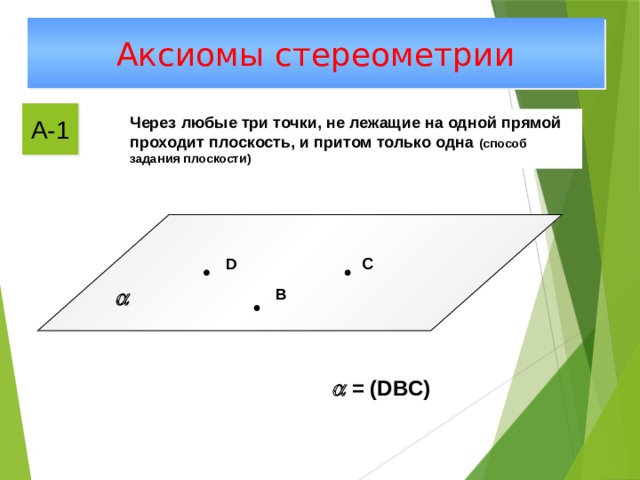
Аксиомы стереометрии

Слово « аксиома » греческого происхождения и в переводе означает истинное, исходное положение теории .

Система аксиом стереометрии дает описание свойств пространства и основных его элементов

Понятия « точка », « прямая », « плоскость », « расстояние » принимаются без определений: их описание и свойства содержатся в аксиомах

Аксиомы стереометрии

А-1

Через любые три точки, не лежащие на одной прямой проходит плоскость, и притом только одна (способ задания плоскости)

D

С

B



 = (DBС)

С

М

m

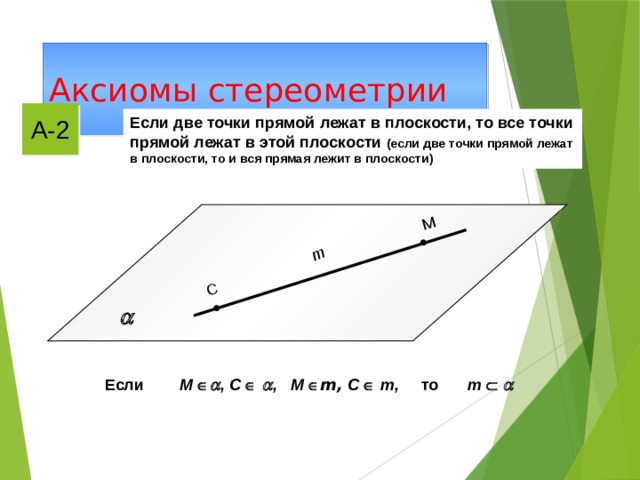
Аксиомы стереометрии

А-2

Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости (если две точки прямой лежат в плоскости, то и вся прямая лежит в плоскости)



М   , C   ,

m  

М  m, C  m,

Если

то

m

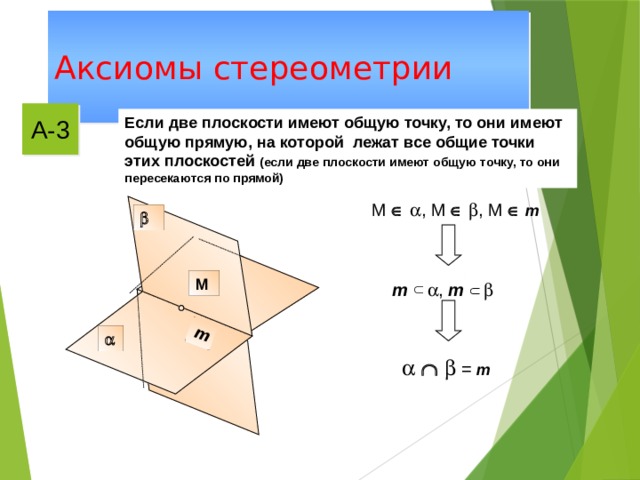
Аксиомы стереометрии

А-3

Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей (если две плоскости имеют общую точку, то они пересекаются по прямой)

М   , М   , М  m



М

m  , m 



   = m

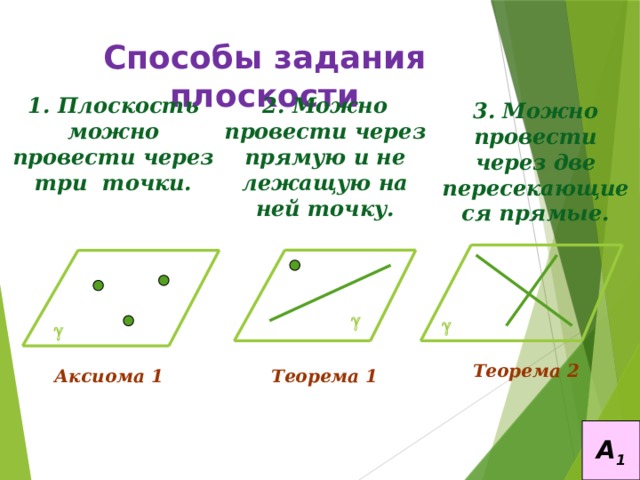
Способы задания плоскости

2. Можно провести через прямую и не лежащую на ней точку.

1. Плоскость можно провести через три точки.

3. Можно провести через две пересекающиеся прямые.

g

g

g

Теорема 2

Аксиома 1

Теорема 1

А 1

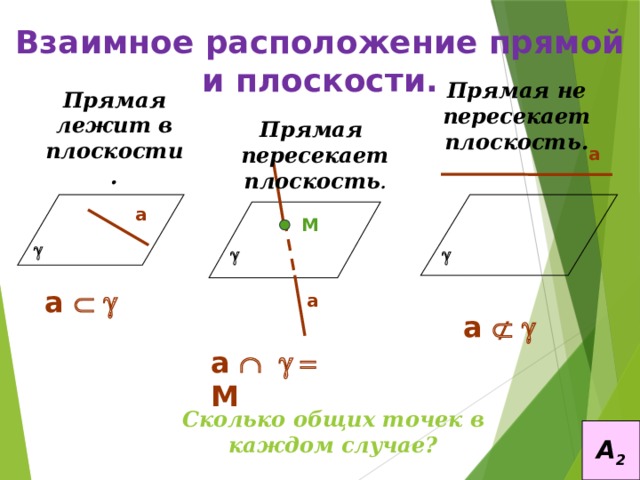
Взаимное расположение прямой и плоскости.

Прямая не пересекает плоскость.

Прямая лежит в плоскости.

Прямая пересекает плоскость .

а

а

М

g

g

g

а Ì g

а

а Ë g

а Ç g = М

Сколько общих точек в каждом случае?

А 2

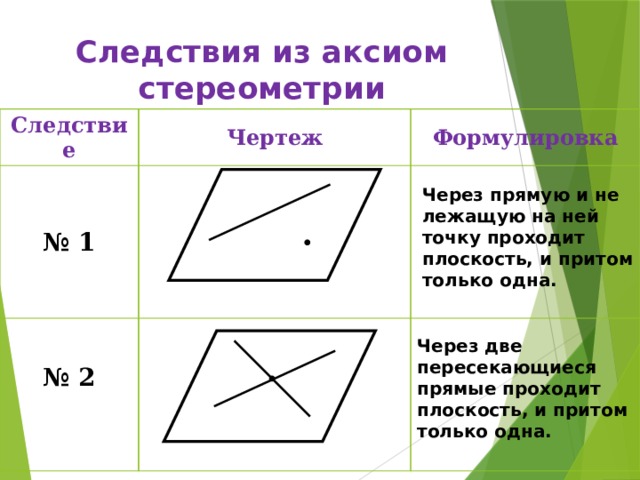
Следствия из аксиом стереометрии

Следствие

Чертеж

№ 1

Формулировка

№ 2

Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна.

Через две пересекающиеся прямые проходит плоскость, и притом только одна.

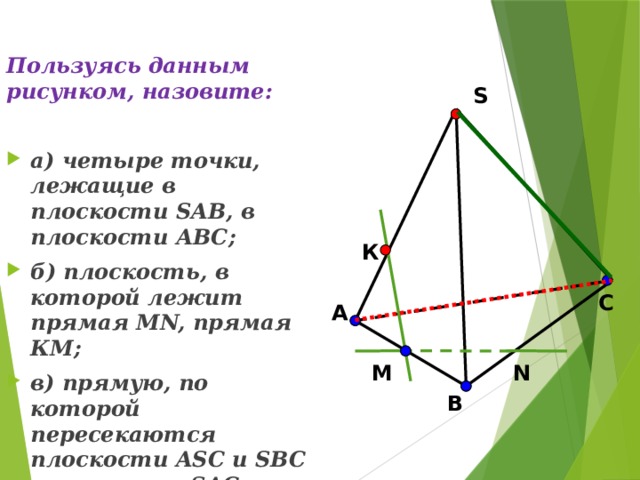
Пользуясь данным рисунком, назовите:

• а) четыре точки, лежащие в плоскости SAB, в плоскости АВС;
• б) плоскость, в которой лежит прямая MN, прямая КМ;
• в) прямую, по которой пересекаются плоскости ASC и SBC , плоскости SAC и CAB.

S

К

C

А

N

М

В

Пользуясь данным рисунком, назовите:

• а) две плоскости, содержащие прямую DE , прямую EF
• б) прямую, по которой пересекаются плоскости

DEF и SBC; плоскости FDE и SAC ;

• в) две плоскости, которые пересекает прямая SB; прямая AC .

S

E

D

С

А

F

В

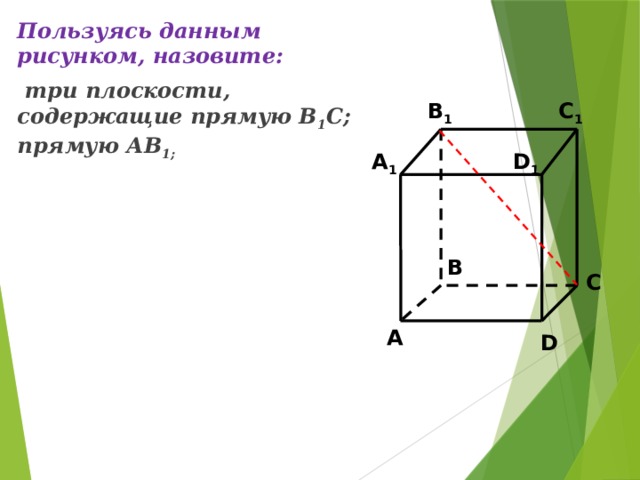
Пользуясь данным рисунком, назовите:

три плоскости, содержащие прямую В 1 С; прямую АВ 1;

C 1

B 1

A 1

D 1

B

C

A

D