Аксиомы стереометрии

Презентация предназначена для систематизации и закрепления знаний по теме "Аксиомы стереометрии", может быть использована на уроках геометрии в 10 классе для закрепления темы и в 11 классе в качестве повтора программы. В презентации приведены кратко и наглядно аксиомы стереометрии и следствия из них.

Презентация содержит вопросы для самоконтроля: "верно ли...", "может ли...", "докажите, что...".

В разделе "Задания для самоконтроля" учащимся предлагается обосновать выбор той или иной точки зрения при ответе на вопросы.

Задания для самоконтроля могут быть использованы на уроке:

1) в качестве обсуждения с учителем или в мини-группах,

2) в виде проверочной работы, а также даны в виде домашнего задания.

Стереометрия  (от др. греч. Στερεός  «стереос» «твёрдый, пространственный» и μετρέω  «измеряю»)  – это  раздел геометрии, в котором изучаются фигуры в пространстве.

Основными фигурами в пространстве являются точка, прямая и плоскость

Аксиомы стереометрии:

Аксиома 1.

Через любые три точки, не лежащие на одной прямой, можно провести плоскость, и притом только одну.

Аксиома 2.

Через прямую и точку, не лежащую на ней, можно провести плоскость, и притом только одну.

Аксиома 3.
Если две плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку.

Аксиомы стереометрии

Содержание :

• Введение
• Аксиомы стереометрии
• Следствия из аксиом
• Задания для самоконтроля

Введение

Стереометрия (от др. греч. Σ τερεός «стереос» «твёрдый, пространственный» и μετρέω   «измеряю»)  – это раздел геометрии, в котором изучаются фигуры в пространстве.

Основными фигурами в пространстве являются

точка, прямая и плоскость

а

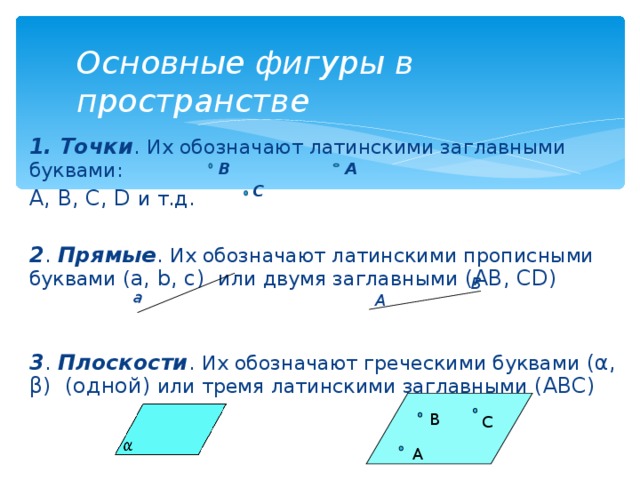
Основные фигуры в пространстве

1. Точки . Их обозначают латинскими заглавными буквами:

A, B, C, D и т.д .

2 . Прямые . Их обозначают латинскими прописными буквами ( a, b, c ) или двумя заглавными ( AB, CD )

3 . Плоскости . Их обозначают греческими буквами ( α , β ) (одной) или тремя латинскими заглавными ( ABC)

В

А

С

В

А

В

С

А

(  ! α ) A  α , B  α , C  α " width="640"

Аксиомы стереометрии

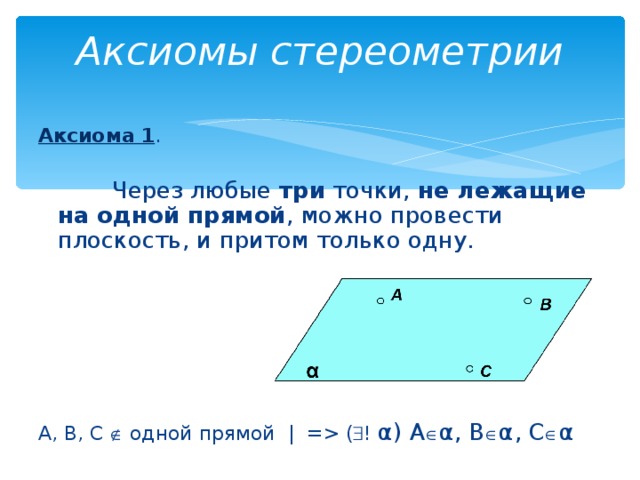
Аксиома 1 .

Через любые три точки, не лежащие на одной прямой , можно провести плоскость, и притом только одну.

A, B, C  одной прямой | = (  ! α ) A  α , B  α , C  α

(  ! β ) A  β , a  β " width="640"

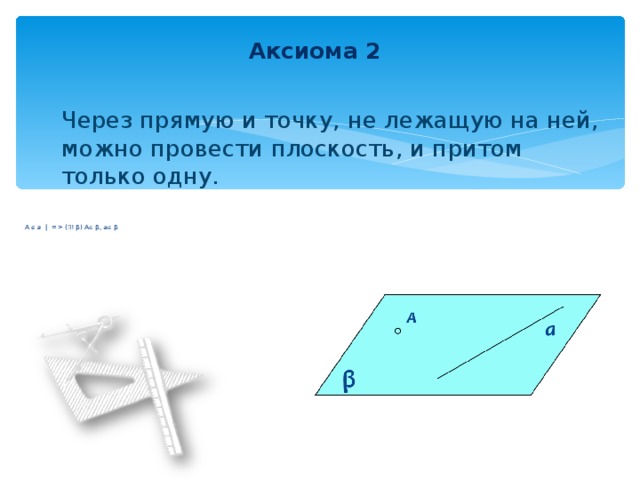
Аксиома 2

Через прямую и точку, не лежащую на ней, можно провести плоскость, и притом только одну.

A  a | = (  ! β ) A  β , a  β

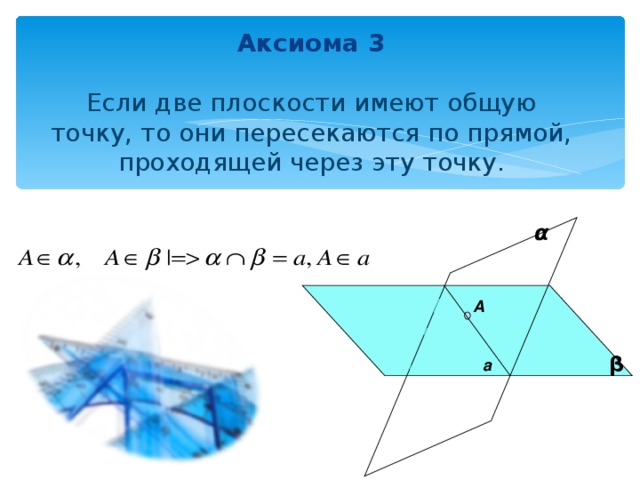
Аксиома 3 Если две плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку.

α

A

β

a

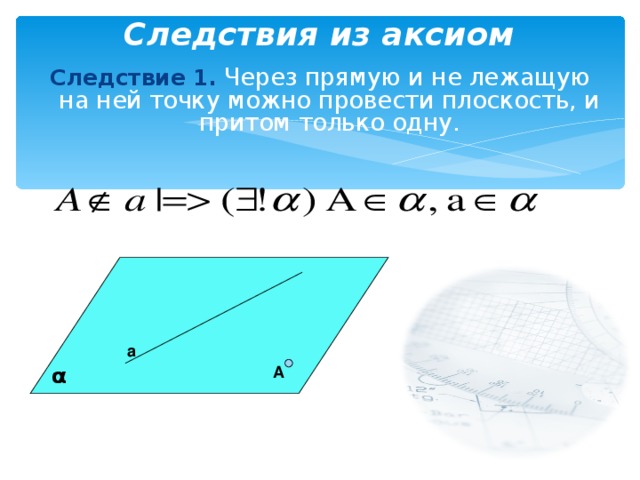
Следствия из аксиом

Следствие 1. Через прямую и не лежащую на ней точку можно провести плоскость, и притом только одну.

a

A

α

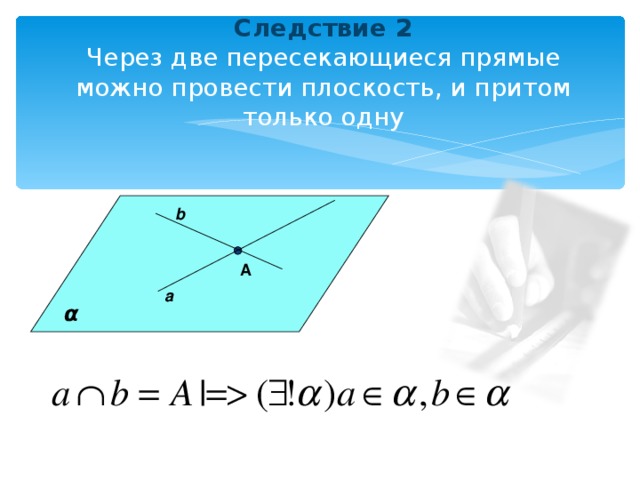
Следствие 2 Через две пересекающиеся прямые можно провести плоскость, и притом только одну

b

A

a

α

Задания для самоконтроля

Задание 1 . Верно ли, что:

• любые три точки лежат в одной плоскости ;
• любые четыре точки не лежат в одной плоскости ;
• любые три точки не лежат в одной плоскости;
• любые четыре точки лежат в одной плоскости ;
• через любые три точки проходит плоскость, и притом только одна ;

Задание 2 . Точки A, B, C, D не лежат в одной плоскости.

• могут ли какие-то три из них лежать на одной прямой?
• могут ли прямые AB и CD пересекаться? Обоснуйте ответ.
• пересекаются ли плоскости, проходящие через точки A, B, C и A, B, D
• могут ли существовать две плоскости, содержащие точки А, В и С, D соответственно ? Если да, то в каких случаях?

Задание 3 . Прямая лежит в плоскости данного треугольника. Может ли она:

а) пересекать две стороны треугольника ;

б) проходить через одну из вершин треугольника?

Задание 4 . Даны прямая и точка, не лежащая на данной прямой. Докажите, что все прямые, проходящие через данную точку и пересекающие данную прямую, лежат в одной плоскости.

Задание 5 . Могут ли две плоскости иметь:

а) только одну общую точку ;

б) только две общие точки ;

в) только одну общую прямую?

Задание 6 . Три точки А , В и С соединены попарно отрезками. Докажите, что все отрезки лежат в одной плоскости.

Задание 7 . Могут ли прямая и плоскость иметь только одну общую точку? Если да, то в каком случае?

Задание 8 . Могут ли прямая и плоскость иметь только две общие точки? Если да, то в каком случае?