Конспект урока "Аксиомы стереометрии"

Цели урока:

Познакомить с понятием стереометрии

Познакомить с аксиомами стереометрии, основные понятия стереометрии

Формирование аккуратности выполнения чертежей

Использовать аксиомы стереометрии при решении задач

Геометрия – это наука, которая изучает свойства геометрических фигур. Геометрическая фигура – это любая совокупность точек. Геометрия подразделяется на планиметрию и на стереометрию, которую мы начинаем изучать.

Основные фигуры с тереометрии, примеры фигур

Основными фигурами стереометрии являются точка, прямая, плоскость. Примеры стереометрических фигур: шар, сфера, конус, цилиндр, параллелепипед и т.д.

 Обозначение основных ф игур стереометрии

А, В, С, D – точки. Точки обозначаются прописными латинскими буквами.

Прямые обозначаются строчными латинскими буквами.

Плоскости обозначаются греческими буквами.

Рассмотрим прямую. На ней лежат точки А и В. Прямая может быть также обозначена как АВ.

Рассмотрим прямую b, на ней лежат точки С и D. Прямая b может быть также обозначена как СD.

Аксиомы стереометрии.

Аксиома 1 (А1)

Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна. 

Рассмотрим три точки: А, В, С, причем точка С не принадлежит прямой АВ: Тогда через три точки А, В, С, не лежащие на одной прямой, проходит плоскость, и притом только одна.

Плоскость можно также обозначить через три точки АВС. 

Аксиома 2 (А2)

Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости. 

По-иному говорят, что прямая лежит в плоскости или что плоскость проходит через прямую. 

Пояснение к аксиоме А2.

Рассмотрим плоскость, точки А, В прямой а принадлежат плоскости

Аксиома утверждает – все точки прямой а (прямой АВ) принадлежат плоскости, т.е. вся прямая лежит в плоскости или плоскость проходит через прямую а. Смысл заключается в следующем: из того, что только две точки принадлежат плоскости, вытекает, что бесчисленное множество точек прямой лежат в этой плоскости.

Следствие: Может ли быть только три общие точки у прямой и плоскости? Нет, не может быть. Может быть две точки, и тогда вся прямая лежит в плоскости.

Весь конспект - смотрите архив.

Урок № 1. (1 четверть Геометрия 10 класс)

Тема: Аксиомы стереометрии и их следствия

Цели урока:

• Познакомить с понятием стереометрии

• Познакомить с аксиомами стереометрии, основные понятия стереометрии

• Формирование аккуратности выполнения чертежей

• Использовать аксиомы стереометрии при решении задач

Геометрия – это наука, которая изучает свойства геометрических фигур. Геометрическая фигура – это любая совокупность точек. Геометрия подразделяется на планиметрию и на стереометрию, которую мы начинаем изучать.

1. Основные фигуры стереометрии, примеры фигур

Основными фигурами стереометрии являются точка, прямая, плоскость. Примеры стереометрических фигур: шар, сфера, конус, цилиндр, параллелепипед и т.д.

1. Обозначение основных фигур стереометрии

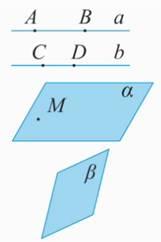
Рис. 1.

А, В, С, D – точки. Точки обозначаются прописными латинскими буквами.

АВ = 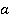, CD = b – прямые. Прямые обозначаются строчными латинскими буквами.

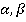 – плоскости. Плоскости обозначаются греческими буквами. (Рис. 1).

Рассмотрим прямую 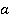. На ней лежат точки А и В. Прямая 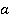может быть также обозначена как АВ.

Рассмотрим прямую b, на ней лежат точки С и D. Прямая b может быть также обозначена как СD.

1. Аксиомы стереометрии.

Аксиома 1 (А1)

Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна. 

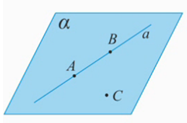
Рис. 2.

Рассмотрим три точки: А, В, С, причем точка С не принадлежит прямой АВ: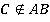 (Рис. 2). Тогда через три точки А, В, С, не лежащие на одной прямой, проходит плоскость 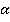, и притом только одна.

Плоскость 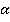можно также обозначить через три точки АВС. 

Аксиома 2 (А2)

Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости. 

По-иному говорят, что прямая лежит в плоскости или что плоскость проходит через прямую. 

Пояснение к аксиоме А2.

Рассмотрим плоскость 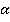, точки А, В прямой 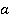принадлежат плоскости 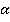(Рис. 3).

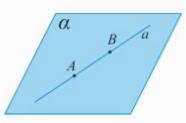
Рис. 3.

Аксиома утверждает – все точки прямой 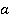(прямой АВ) принадлежат плоскости 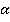, т.е. вся прямая лежит в плоскости 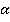или плоскость 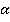проходит через прямую 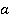. Смысл заключается в следующем: из того, что только две точки принадлежат плоскости, вытекает, что бесчисленное множество точек прямой лежат в этой плоскости.

Эту аксиому можно записать следующим образом:

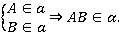
Следствие: Может ли быть только три общие точки у прямой и плоскости? Нет, не может быть. Может быть две точки, и тогда вся прямая лежит в плоскости.

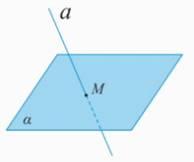
Если у прямой и плоскости одна общая точка М, то тогда говорят, что прямая 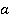и плоскость 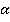пересекаются в точке М (Рис. 4). Этот факт записывается следующим образом: .

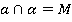Аксиома 3 (А3)

Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей. Говорят, что плоскости пересекаются по прямой. 

Пояснение к аксиоме А3.

Имеем разные плоскости: плоскость 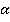, плоскость 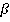. Известно, что они имеют общую точку М, точка М принадлежит плоскости и плоскости 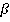. (Рис. 5)

Рис. 5.

Отсюда вытекает, что существует прямая 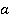, которая проходит через точку М, которая одновременно принадлежит и плоскости a, и плоскости b. Вот в этом случае и говорят, что плоскост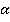и и 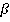пересекаются по прямой .

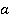Смысл аксиом разъясняется в многочисленных вопросах и задачах. Вот некоторые из них. 

мысл аксиом разъясняется в многочисленных вопросах и задачах. Вот некоторые из них. 

Решение задач

Дан тетраэдр АВСD (Рис. 6). Даны следующие точки: точка Е – внутренняя точка ребра АВ, точка Р – внутренняя точка отрезка ЕD, точки М и К, соответственно, на ребрах ВD и DС.

Рис. 6. 

Задача 1

а) В какой плоскости лежит прямая

Ответ: . Прямая РЕ лежит в плоскости АВD, так как в этой плоскости лежат две точки этой прямой. Точка Е лежит в плоскости АВD и точка Р лежит в этой же плоскости. Значит, по второй аксиоме все точки прямой РЕ лежат в плоскости АВD.

 б) В какой плоскости лежит прямая

Ответ: . Прямая MK лежит в плоскости DBC, так как в этой плоскости лежат две точки этой прямой. Точка M лежит в плоскости DBC и точка Р лежит в плоскости DBC. По второй аксиоме все точки прямой MK лежат в плоскости DBC.

 в) В каких плоскостях лежит прямая

Ответ: Прямая BD лежит в плоскостиBDА и в плоскости BDС. Значит, прямая BD одновременно лежит в двух плоскостях. Прямая BD есть линия пересечения двух плоскостей. Говорят, что грани АBD, BDС пересекаются по прямой BD. Это можно записать так:

.

г) В каких гранях лежит прямая ?

Ответ: Прямая АB лежит в грани АВС и в грани АBD. Значит, прямая АВ есть линия пересечения двух этих граней.

д) В каких гранях лежит прямая ?

Ответ: Прямая EC лежит в плоскости АВС и в плоскости ECD, так как точки Е и С лежат одновременно в плоскости АВС и в плоскости ECD. Значит, прямая ЕС есть линия пересечения этих плоскостей. 

Задача 2.

а) Найдите точку пересечения прямой DК с плоскостью АВС.

Решение:

Прямая DК содержит точку С. Плоскость АВС содержит точку С. Значит, прямая DК и плоскость АВС пересекаются в точке С.

б) Найдите точку пересечения прямой СЕ с плоскостью АDВ.

Решение: 

Точка Е принадлежит и прямой СЕ, и плоскости АDВ. Значит, Прямая СЕ пересекается с плоскостью АDВ в точке Е. 

Задача 3.

а) Найдите точки, лежащие одновременно в плоскостях АDВ и DВС.

Решение:

Точка В и точка D одновременно лежат и в АDВ, и в DВС. Значит, . Все точки прямой DВ являются ответом. 

б) Найдите прямые, по которым пересекаются плоскость АDВ и DВС.

Решение:

Точка В и точка D одновременно лежат и в АDВ, и в DВС. Значит, прямая DВ есть прямая, по которой пересекаются заданные плоскости. 

в) Назовите прямые, по которым пересекаются плоскости АDВ и СDА.

Решение:

Точки А, D лежат в плоскости АDВ, а также точки А, D лежат в другой плоскости СDА. Значит, АD – линия их пересечения: . 

г) Назовите прямые, по которым пересекаются плоскости РDС и АВС.

Решение: 

Плоскость РDС совпадает с плоскостью ЕDС. Точка Е и точка С одновременно лежат в двух плоскостях: РDС и АВС. Значит, СЕ – это линия пересечения двух плоскостей.  

1. Домашнее задание: Выучить аксиомы А1 – А3, п.1 – 2, №2(б,д)  

Рис 7.