Аксиомы стереометрии

Стереометрия - раздел  геометрии,  в  котором изучаются свойства  фигур в пространстве.

Геометрические понятия.

Плоскость – грань

Прямая – ребро

Точка – вершина

Аксиома (от греч. axíõma – принятие положения) - исходное положение научной теории, принимаемое без доказательства.

А1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна

А2. Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости

А3. Если две плоскости имеют общую  точку, то  они имеют общую прямую, на которой лежат все общие точки этих плоскостей.

Аксиомы

стереометрии .

Некоторые

следствия

из аксиом.

Геометрия

Планиметрия

Стереометрия

stereos

телесный, твердый, объемный, пространственный

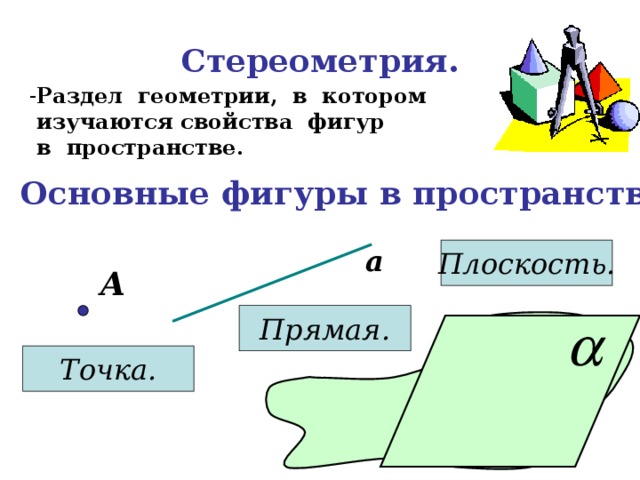
Стереометрия.

• Раздел геометрии, в котором

изучаются свойства фигур

в пространстве.

Основные фигуры в пространстве:

а

Плоскость.

А

Прямая.

Точка.

A, B, C, …

a, b, c, …

A В , B С , CD, …

или

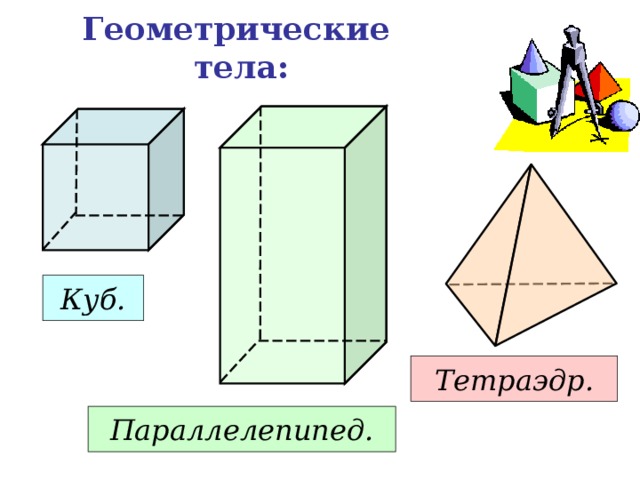
Геометрические тела:

Куб.

Тетраэдр.

Параллелепипед.

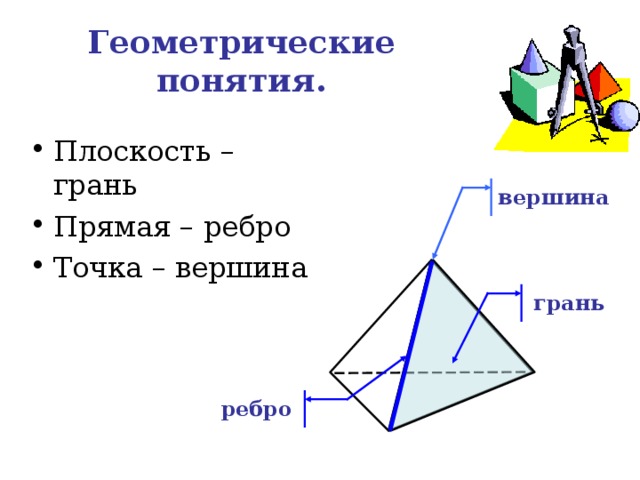
Геометрические понятия.

• Плоскость – грань
• Прямая – ребро
• Точка – вершина

вершина

грань

ребро

Аксиома

(от греч. ax íõ ma – принятие положения)

исходное положение научной теории, принимаемое без доказательства

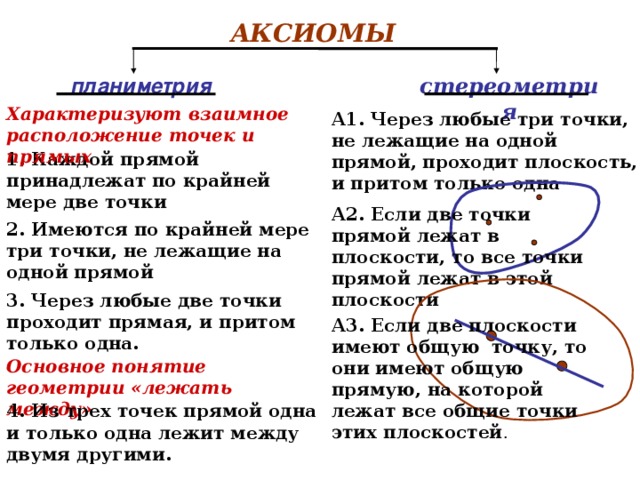
АКСИОМЫ

планиметрия

стереометрия

Характеризуют взаимное расположение точек и прямых

А1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна

1. Каждой прямой принадлежат по крайней мере две точки

А2. Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости

2. Имеются по крайней мере три точки, не лежащие на одной прямой

3. Через любые две точки проходит прямая, и притом только одна.

А3. Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей .

Основное понятие геометрии «лежать между»

4. Из трех точек прямой одна и только одна лежит между двумя другими.

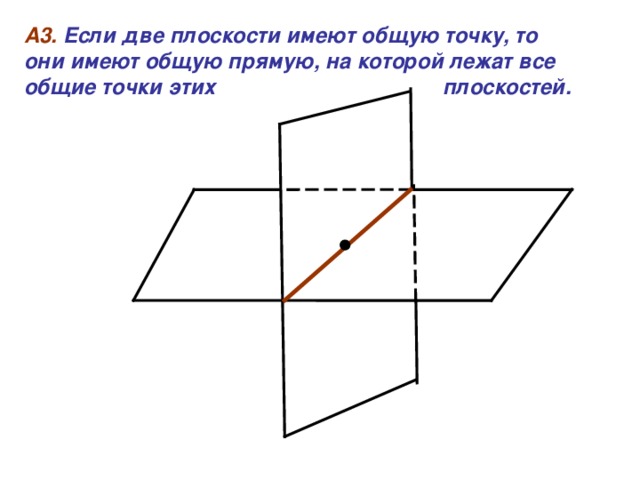
А3. Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.

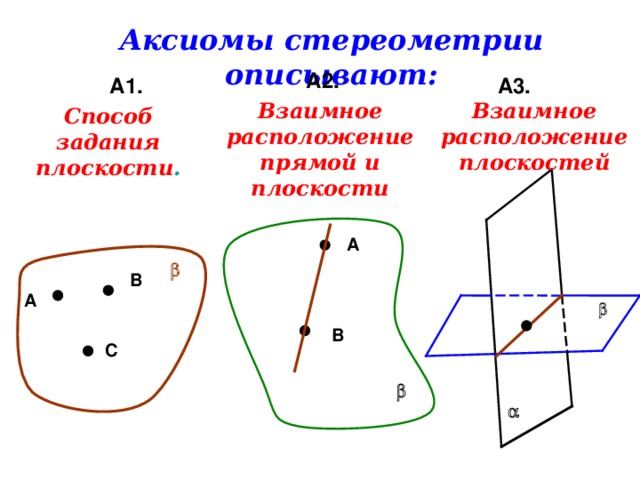
Аксиомы стереометрии описывают:

А2.

А1.

А3.

Взаимное расположение плоскостей

Взаимное расположение прямой и плоскости

Способ задания плоскости .

А



В

А



В

С





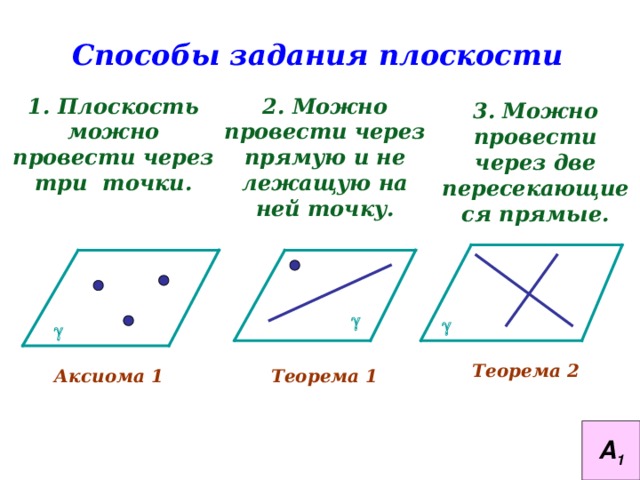
Способы задания плоскости

2. Можно провести через прямую и не лежащую на ней точку.

1. Плоскость можно провести через три точки.

3. Можно провести через две пересекающиеся прямые.







Теорема 2

Аксиома 1

Теорема 1

А 1

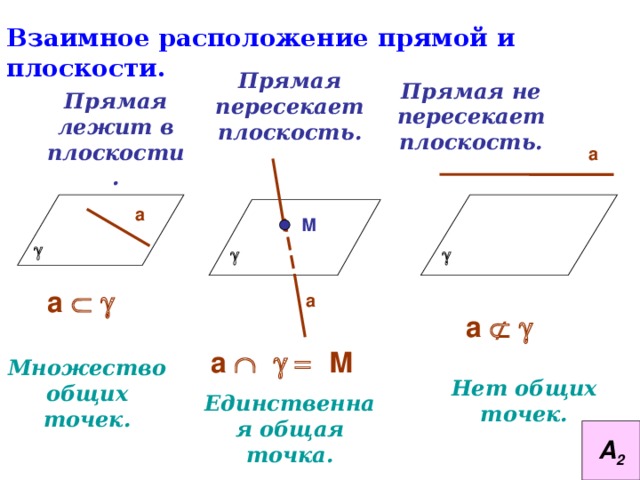
Взаимное расположение прямой и плоскости.

Прямая пересекает плоскость.

Прямая не пересекает плоскость.

Прямая лежит в плоскости.

а

а

М







а 

а

а 

а  М

Множество общих точек.

Нет общих точек.

Единственная общая точка.

А 2

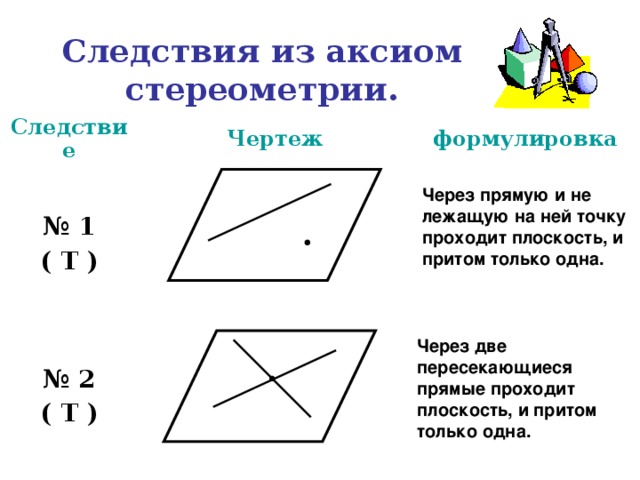
Следствия из аксиом стереометрии.

Следствие

Чертеж

№ 1

( Т )

формулировка

№ 2

( Т )

Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна.

Через две пересекающиеся прямые проходит плоскость, и притом только одна.

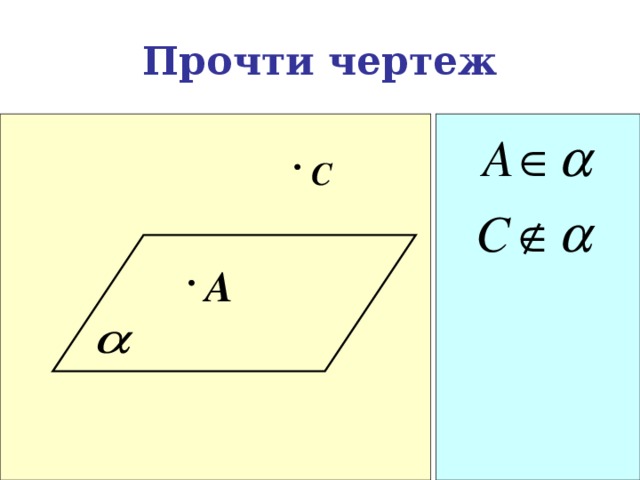
Прочти чертеж

С

A

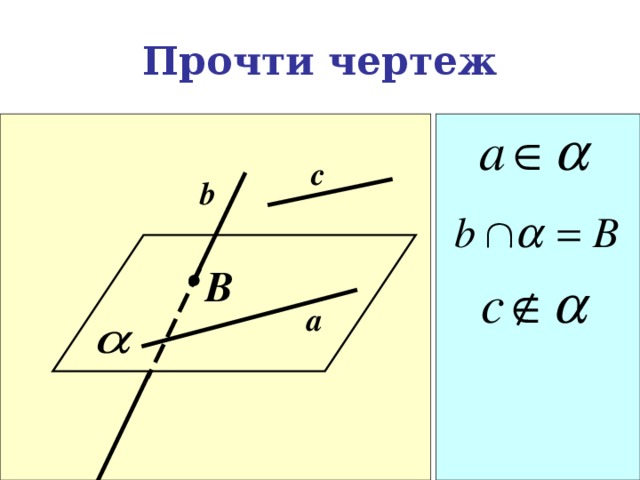
Прочти чертеж

c

b

B

a

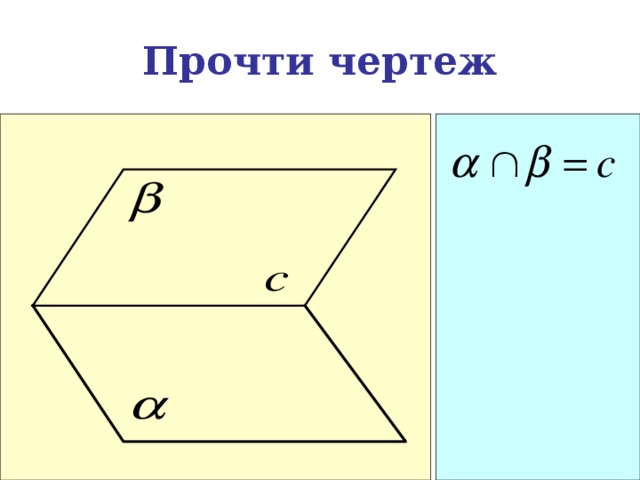
Прочти чертеж

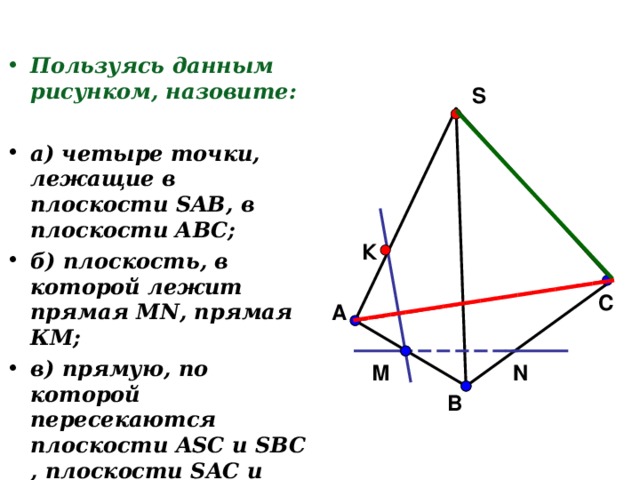
• Пользуясь данным рисунком, назовите:

• а) четыре точки, лежащие в плоскости SAB , в плоскости АВС;
• б) плоскость, в которой лежит прямая MN , прямая КМ;
• в) прямую, по которой пересекаются плоскости ASC и SBC , плоскости SAC и CAB .

S

К

C

А

N

М

В

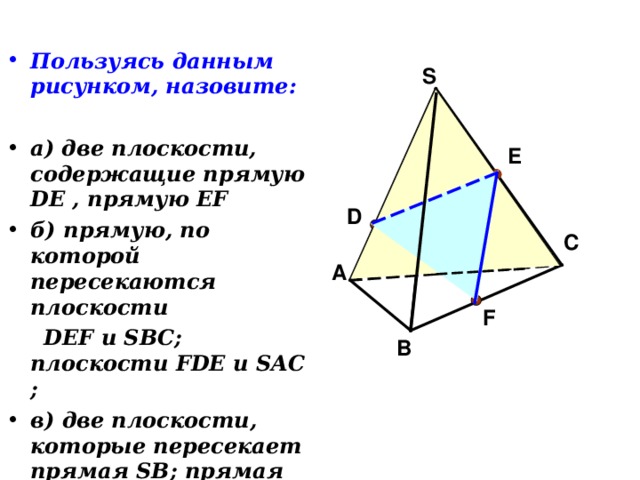
• Пользуясь данным рисунком, назовите:

• а) две плоскости, содержащие прямую DE , прямую EF
• б) прямую, по которой пересекаются плоскости

DEF и SBC ; плоскости FDE и SAC ;

• в) две плоскости, которые пересекает прямая SB ; прямая AC .

S

E

D

С

А

F

В

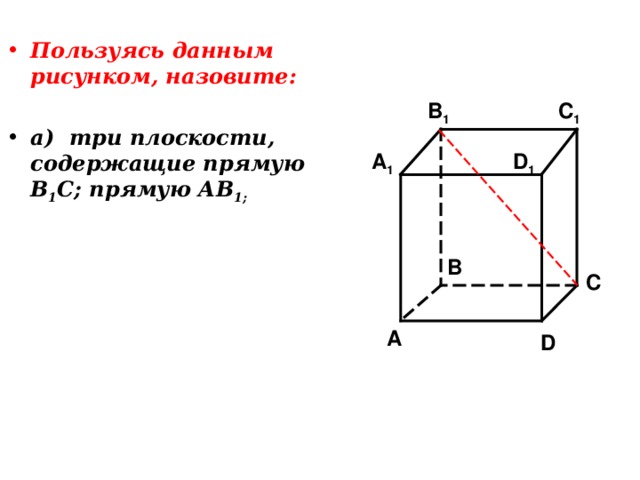
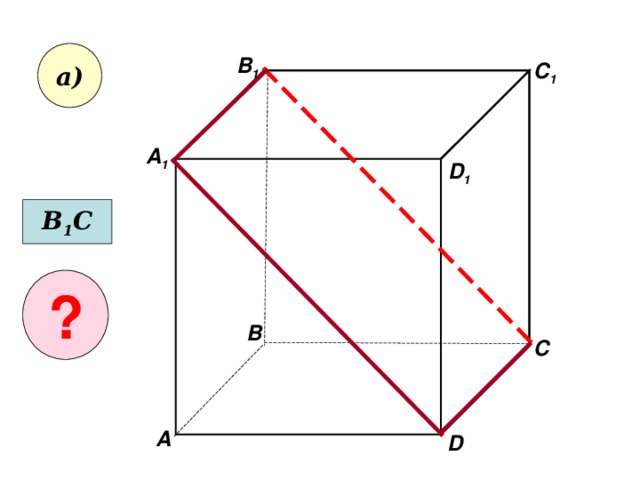
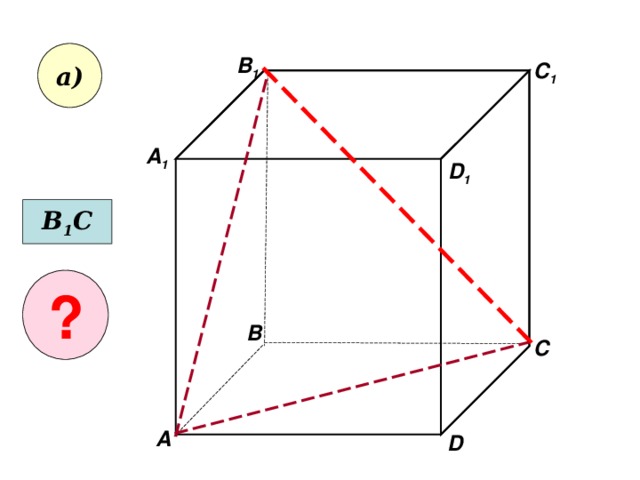
• Пользуясь данным рисунком, назовите:

• а) три плоскости, содержащие прямую В 1 С; прямую АВ 1;

C 1

B 1

A 1

D 1

B

C

A

D

а)

В 1

C 1

А 1

D 1

В 1 С

?

В

С

А

D

а)

В 1

C 1

А 1

D 1

В 1 С

?

В

С

А

D

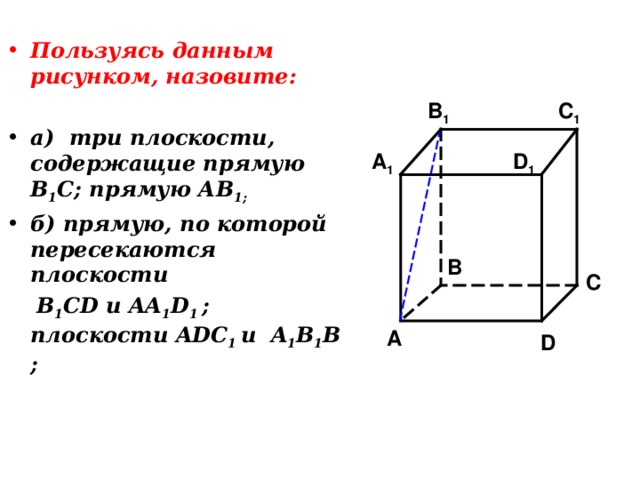
• Пользуясь данным рисунком, назовите:

• а) три плоскости, содержащие прямую В 1 С; прямую АВ 1;
• б) прямую, по которой пересекаются плоскости

B 1 CD и AA 1 D 1 ; плоскости ADC 1 и A 1 B 1 B ;

C 1

B 1

A 1

D 1

B

C

A

D

б)

В 1

C 1

А 1

D 1

В

С

А

D

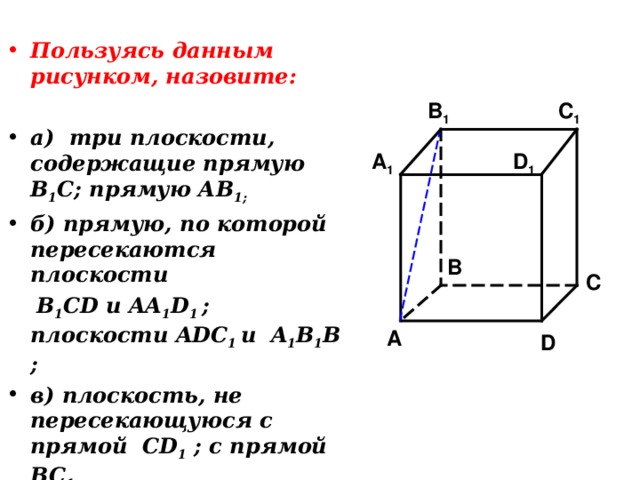
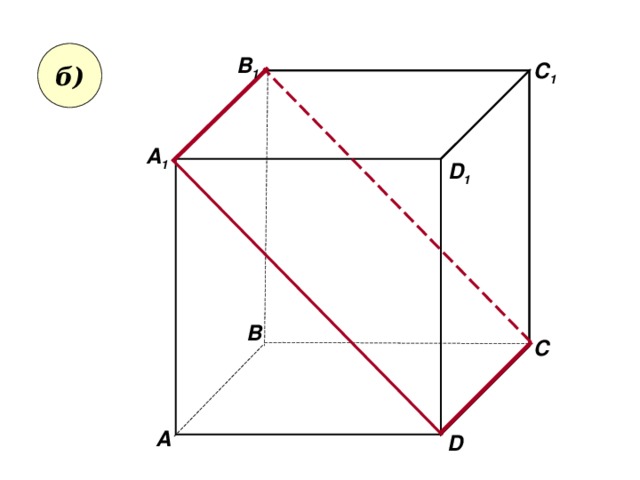
• Пользуясь данным рисунком, назовите:

• а) три плоскости, содержащие прямую В 1 С; прямую АВ 1;
• б) прямую, по которой пересекаются плоскости

B 1 CD и AA 1 D 1 ; плоскости ADC 1 и A 1 B 1 B ;

• в) плоскость, не пересекающуюся с прямой CD 1 ; с прямой BC 1

C 1

B 1

A 1

D 1

B

C

A

D

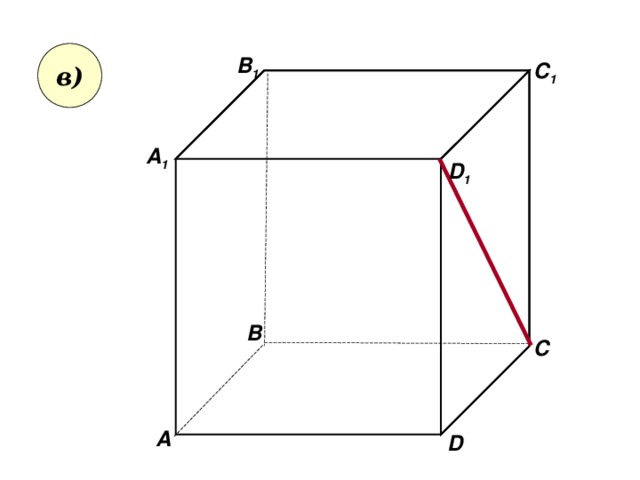
в)

В 1

C 1

А 1

D 1

В

С

А

D

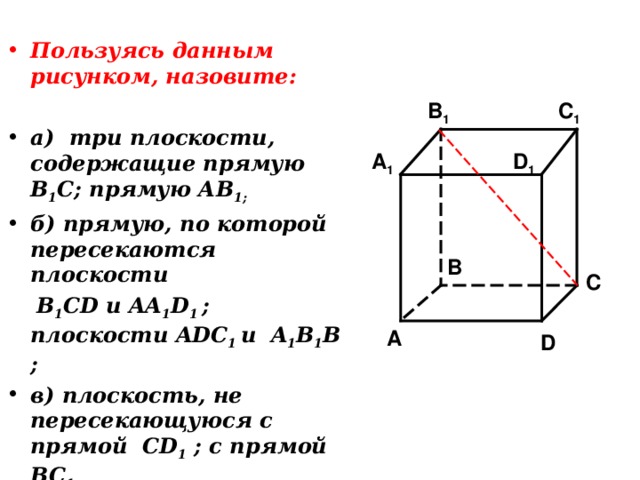
• Пользуясь данным рисунком, назовите:

• а) три плоскости, содержащие прямую В 1 С; прямую АВ 1;
• б) прямую, по которой пересекаются плоскости

B 1 CD и AA 1 D 1 ; плоскости ADC 1 и A 1 B 1 B ;

• в) плоскость, не пересекающуюся с прямой CD 1 ; с прямой BC 1

C 1

B 1

A 1

D 1

B

C

A

D

Закрепление изученного материала.

• № 1;
• № 2 (б,д);

Домашнее задание:

• Выучить аксиомы

и следствия из них.

Задания 4 – 12 в

рабочей тетради.

3) №№ 4; 6; 10.

Успехов!

2) П. 1-3

стр. 4 – 7.

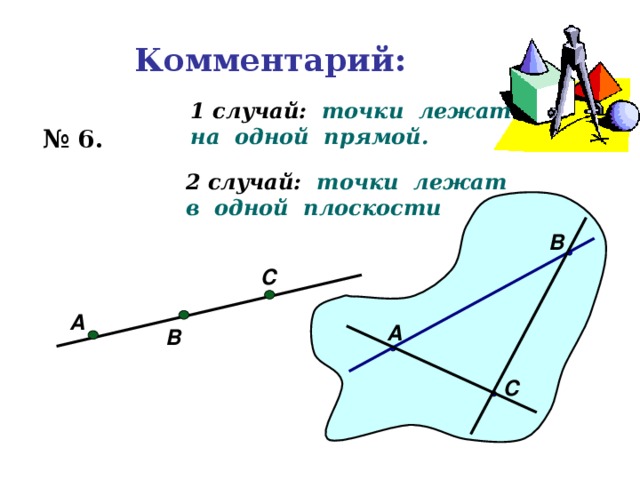
Комментарий:

1 случай: точки лежат

на одной прямой.

№ 6.

2 случай: точки лежат

в одной плоскости

В

С

А

А

В

С