Аксиомы стереометрии

Планиметрия - это раздел геометрии, в котором изучаются свойства фигур на плоскости

Стереометрия - это раздел геометрии, в котором изучаются свойства фигур в пространстве.

АКСИОМЫ

А1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна

А2. Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости

А3. Если две плоскости имеют общую  точку, то  они имеют общую прямую, на которой лежат все общие точки этих плоскостей.

Тема: Аксиомы стереометрии.

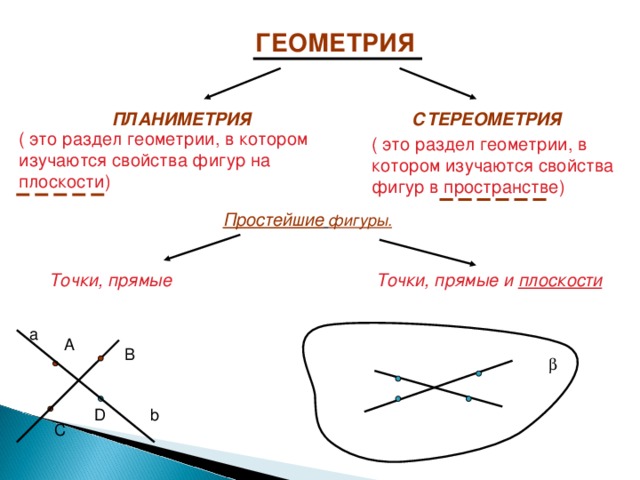
ГЕОМЕТРИЯ

СТЕРЕОМЕТРИЯ

ПЛАНИМЕТРИЯ

( это раздел геометрии, в котором изучаются свойства фигур на плоскости)

( это раздел геометрии, в котором изучаются свойства фигур в пространстве)

Простейшие фигуры.

Точки, прямые

Точки, прямые и плоскости

a

А

В



D

b

С

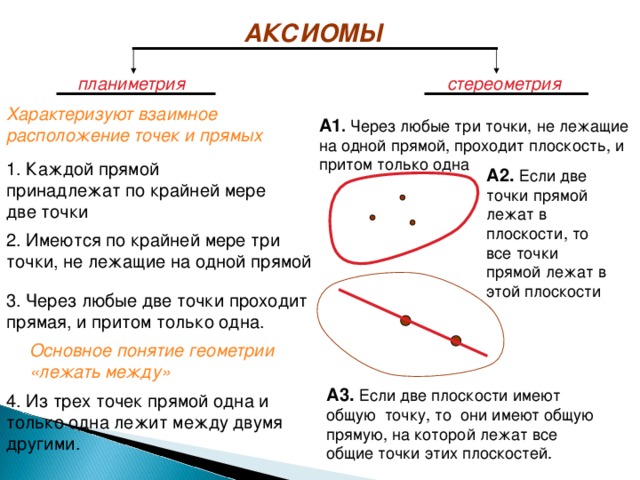
АКСИОМЫ

планиметрия

стереометрия

Характеризуют взаимное расположение точек и прямых

А1 . Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна

1. Каждой прямой принадлежат по крайней мере две точки

А2. Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости

2. Имеются по крайней мере три точки, не лежащие на одной прямой

3. Через любые две точки проходит прямая, и притом только одна.

Основное понятие геометрии «лежать между»

А3. Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.

4. Из трех точек прямой одна и только одна лежит между двумя другими.

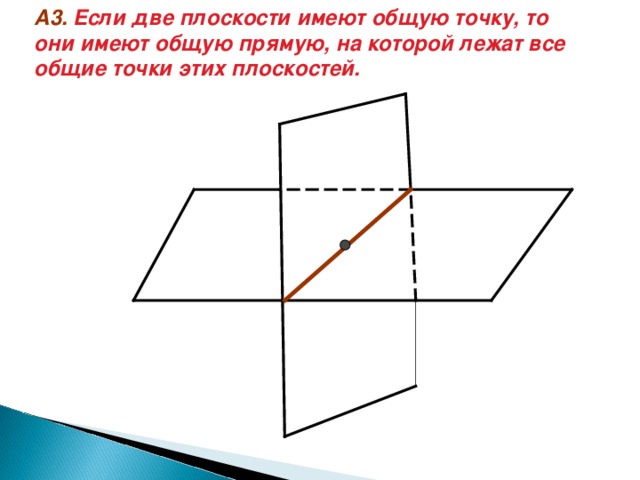
А3. Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.

АКСИОМЫ

планиметрия

стереометрия

Характеризуют взаимное расположение точек и прямых

А1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна

1. Каждой прямой принадлежат по крайней мере две точки

А2. Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости

2. Имеются по крайней мере три точки, не лежащие на одной прямой

А3. Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.

3. Через любые две точки проходит прямая, и притом только одна.

Основное понятие геометрии «лежать между»

4. Из трех точек прямой одна и только одна лежит между двумя другими.

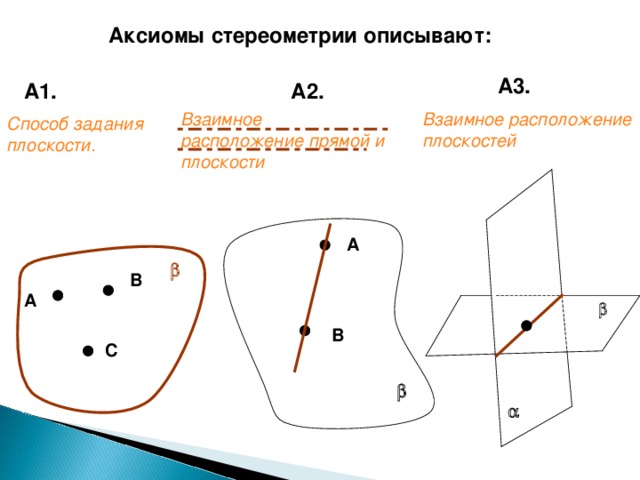
Аксиомы стереометрии описывают:

А3.

А2.

А1.

Взаимное расположение прямой и плоскости

Взаимное расположение плоскостей

Способ задания плоскости.

А



В

А



В

С





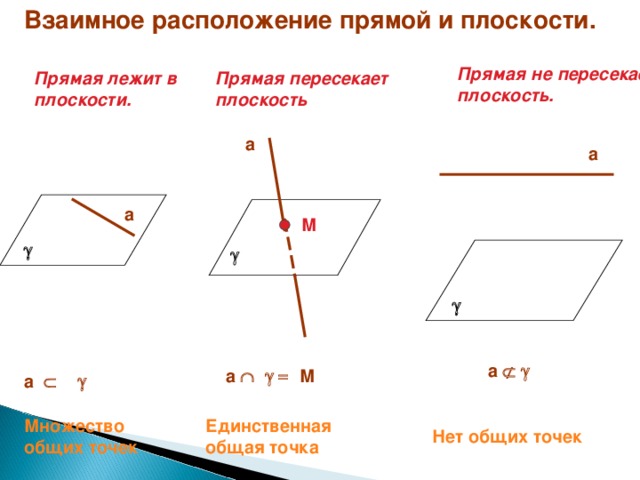
Взаимное расположение прямой и плоскости.

Прямая не пересекает плоскость.

Прямая лежит в плоскости.

Прямая пересекает плоскость

а

а

а

М







а 

а  М

а 

Множество общих точек

Единственная общая точка

Нет общих точек

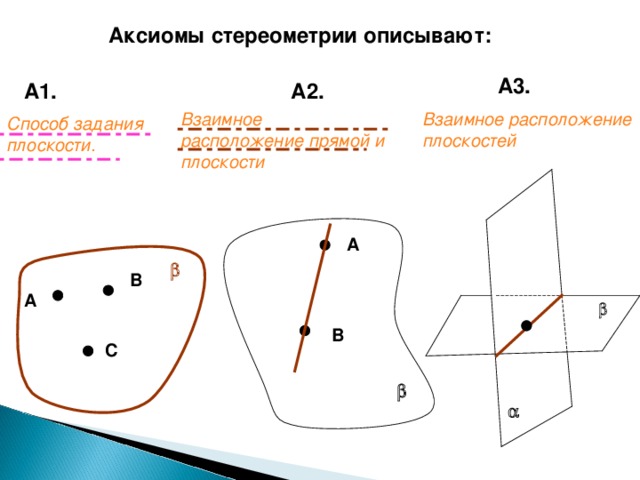
Аксиомы стереометрии описывают:

А3.

А1.

А2.

Взаимное расположение прямой и плоскости

Взаимное расположение плоскостей

Способ задания плоскости.

А



В

А



В

С





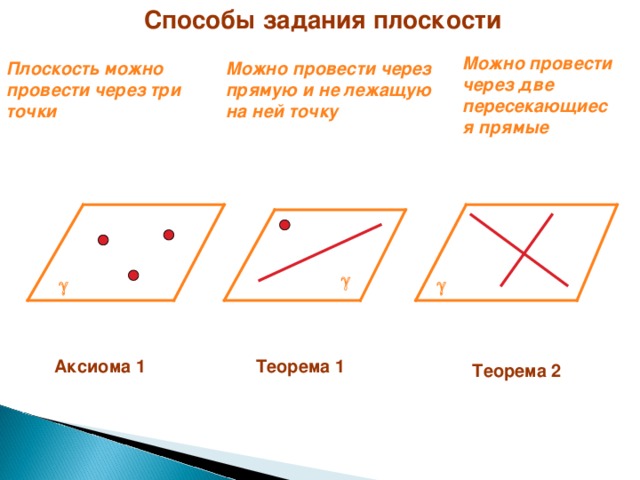
Способы задания плоскости

Можно провести через две пересекающиеся прямые

Можно провести через прямую и не лежащую на ней точку

Плоскость можно провести через три точки







Аксиома 1

Теорема 1

Теорема 2

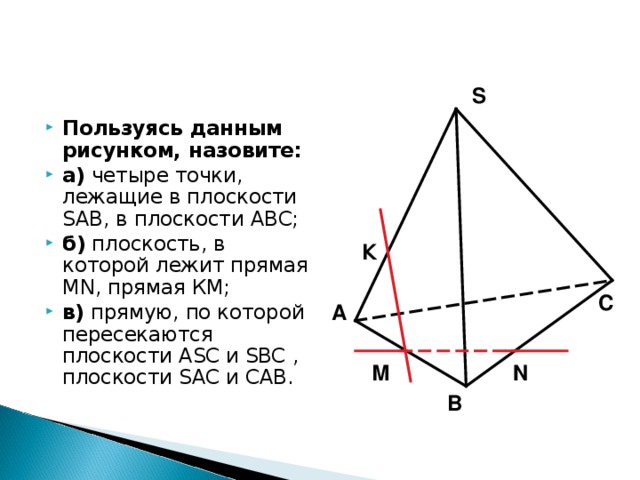
S

• Пользуясь данным рисунком, назовите:
• а) четыре точки, лежащие в плоскости SAB , в плоскости АВС;
• б) плоскость, в которой лежит прямая MN , прямая КМ;
• в) прямую, по которой пересекаются плоскости ASC и SBC , плоскости SAC и CAB .

К

C

А

М

N

В

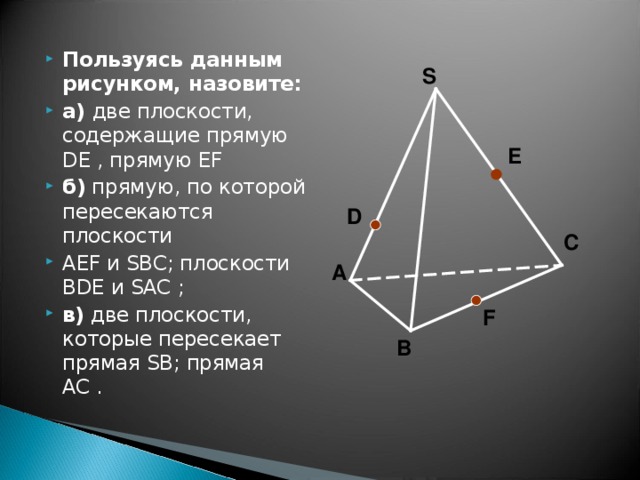
• Пользуясь данным рисунком, назовите:
• а) две плоскости, содержащие прямую DE , прямую EF
• б) прямую, по которой пересекаются плоскости
• AEF и SBC ; плоскости BDE и SAC ;
• в) две плоскости, которые пересекает прямая SB ; прямая AC .

S

E

D

С

А

F

В

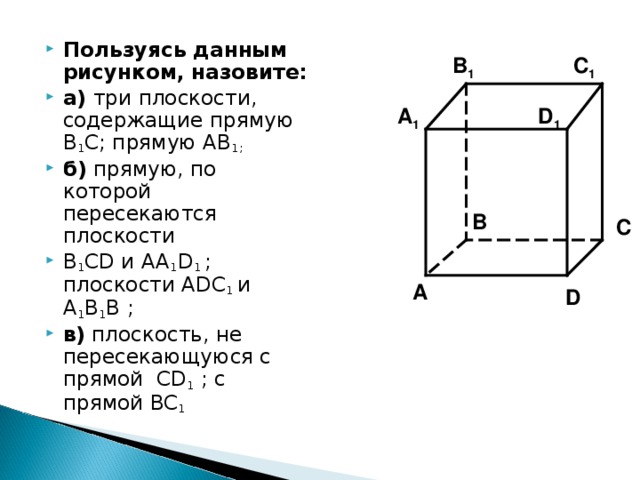
• Пользуясь данным рисунком, назовите:
• а) три плоскости, содержащие прямую В 1 С; прямую АВ 1;
• б) прямую, по которой пересекаются плоскости
• B 1 CD и AA 1 D 1 ; плоскости ADC 1 и A 1 B 1 B ;
• в) плоскость, не пересекающуюся с прямой CD 1 ; с прямой BC 1

B 1

C 1

A 1

D 1

B

C

A

D