Урок № 44
Тема: «Треугольники. Теорема о соотношениях между сторонами и углами треугольника.»
7а –
7б -
7г –
7е -
Тип урока: ознакомление с новым материалом
Цель урока: организовать деятельность обучающихся по восприятию следствий из теоремы о соотношениях между сторонами и углами треугольника, их доказательству, осмыслению и применению в решении задач.
Задачи урока:
Предметные: повторить понятие треугольника, классифицировать его по сторонам, сформулировать и доказать теорему о соотношениях между сторонами и углами треугольника, следствия из неё. Научить применять доказанные утверждения в задачах.
Личностные: Воспитывать интерес к геометрии, культуру устной речи, правильное и аккуратное оформление геометрических задач.
Метапредметные: Развивать логическое и пространственное воображение, интуицию учащихся; формировать умения чётко и ясно излагать свои мысли; совершенствовать графическую культуру.
Планируемые результаты:
Предметные: познакомятся со следствиями из теоремы о соотношениях между сторонами и углами треугольника.
Личностные: Проявляют устойчивый и широкий интерес к способам решения познавательных задач, положительное отношение к урокам математики, дают оценку результатов своей учебной деятельности.
Метапредметные:
Р – определяют цель учебной деятельности, осуществляют поиск средств её осуществления.
П – делают предположения об информации, которая нужна для решения учебной задачи.
К – умеют отстаивать точку зрения, аргументируя ее, подтверждая фактами.
Оборудование: мультимедийный проектор; компьютер, интерактивная доска.
Структура урока:
| 1. | Организационный момент | 2 мин |
| 2 | Проверка д.з. | 3 мин |
| 3. | Подготовка к изучению нового материала, через актуализацию опорных знаний | 4мин |
| 4. | Формулирование темы и цели урока | 1 мин |
| 5. | Ознакомление с новым материалом | 15 мин |
| 6. | Физкультминутка | 1 мин |
| 7. | Первичное осмысление и закрепление связей и отношений в объектах изучения | 15 мин |
| 8. | Рефлексия | 1 мин |
| 9. | Постановка Д/З | 1мин |
Ход урока
| Учитель | Ученики | УУД | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Организационный момент |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Приветствие обучающихся Эпиграф нашего урока: «Высшее проявление духа – это разум. Высшее проявление разума – это геометрия, клетка геометрии – треугольник. Он так же неисчерпаем, как и Вселенная.» | Приветствуют учителя.
| К: Умение слушать и вступать в диалог. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 2. Проверка д.з. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Есть ли вопросы по д.з.?
| задают вопросы. | К: Умение слушать и вступать в диалог. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Подготовка к изучению нового материала, через актуализацию опорных знаний |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Двое учащихся готовят у доски доказательства I и II частей теоремы о соотношениях между сторонами и углами треугольника с последующим заслушиванием их ответов всем классом. (слайд 1)
(слайд 2)
Вспомним: - определение внешнего угла треугольника, свойство. - теорема о сумме углов треугольника.
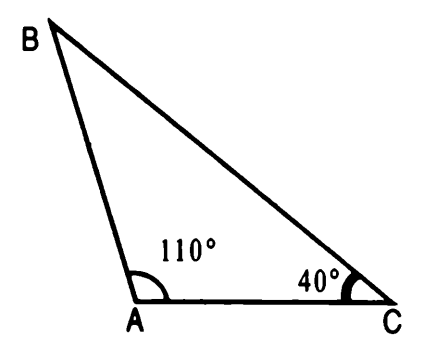
ТЕСТ (слайд 3) 1.Существует ли треугольник с углами 47°, 56°, 87° 78°, 64°, 38° 2.Напротив какой стороны лежит больший угол? 48 см, 49 см, 2 см 15 дм, 42 дм, 26 дм 3. Какая сторона лежит напротив Тупого угла прямого угла а) наибольшая; б) наименьшая; в) средняя; г) нельзя определить 4. Определите вид треугольника, если известно, что у него один внешний угол Прямой острый а) прямоугольный, б) тупоугольный, в) остроугольный, г) нельзя определить 5. Является ли треугольник равнобедренным, если два его угла равны 40°, 100° 50°, 100° Взаимопроверка (слайд 4)
-Как вы можете сформулировать тему урока?
| отвечают
ВС наибольшая, АС наименьшая
| П: уметь ориентироваться в своей системе знаний К: уметь слушать и понимать речь других, оформлять мысли в устной речи Р: уметь проговаривать последовательность действий на уроке, высказывать свое предположение | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Формулирование темы и цели урока | | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Постановка цели урока - Какую цель мы поставим перед собой? - А какие задачи мы с вами определим? - Приступим к выполнению заданий для достижения поставленной цели. | Формулируют, записывают в тетрадях число, кл/р, тема урока. |
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Ознакомление с новым материалом | | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
№ 243 Дано: ΔАВС, АА1- биссектриса ∠A, CD || АА1, CD ∩ AB = D. Доказать: АС = AD. Доказательство: 1) ∠1 = ∠2 (т.к. AA1 - биссектриса ∠A) 2) ∠1 = ∠3 (соответственные углы при CD || АА1 и секущей ВD) 3) ∠4 = ∠2 (накрест лежащие углы при CD || АА1 и секущей АС) 4) Рассмотрим ΔАDC: ∠3 = ∠4 (см. п. 1-3). Следовательно, АС = AD (по признаку р/б треугольника), что и требовалось доказать.
| Записывают следствие и доказательство
Делают вывод
Один ученик у доски остальные в тетрадях.
| П: уметь добывать новые знания. Р: уметь работать по коллективно составленному плану, проговаривать последовательность действий на уроке. К: уметь слушать и понимать других, оформлять свои мысли в устной и письменной речи | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 5. Физкультминутка | | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 1. Потереть ладонью о ладонь. Закрыть глаза и положить ладони на них. Отдых 10-15 с. | выполняют |
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 6. Первичное осмысление и закрепление связей и отношений в объектах изучения |
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| № 240. Дано: ΔАВС – р/б, АВ = ВС, АО - биссектриса ∠A, СО - биссектриса ∠C, АО Доказать: ΔАОС - равнобедренный.
Доказательство: 1) Так как ΔАВС - равнобедренный, то ∠A = ∠C (по свойству р/б треугольника). 2) ∠1 = ∠2 = ∠3 = ∠4 (так как АО, СО - биссектрисы соответственно равных углов). 3) Рассмотрим ΔАОС: ∠2 = ∠3 (см. п.2), тогда АО = СО (по признаку р/б треугольника). Значит, ΔАОС - равнобедренный (по определению). Что и требовалось доказать.
№ 241
№ 246. Дано: ΔАВС, ВО и ОС - биссектрисы, OE || AB, OD || AC. Доказать: Р△OED = ВС.
Доказательство: 1) ∠1 = ∠3, как накрест лежащие углы при ОЕ || АВ и секущей ОВ, ∠1 = ∠2, так как ВО – биссектриса угла В, ∠2 = ∠3, тогда 2) ∠4 = ∠6, как накрест лежащие углы при OD || АС и секущей ОС, ∠4 = ∠5, так как СО - биссектриса, ∠5 = ∠6, значит,
№ 247 Дано: АВ = АС, АР = АQ
Тр.док: а) △ВОС – р/б; б) ВК=КС, АК┴ВС Док-во: а) Рассмотрим △СВQ и △ВСP: BC – общая QC = AC – AQ=АВ – АР= ВР Значит, △СВQ = △ВСP (по двум сторонам и углу между ними), следовательно Значит, △ВОС – р/б (по признаку равнобедренного треугольника), что и требовалось доказать. б) Рассмотрим △АВО и △АОС: АО– общая АВ = ВС (по условию) ВО = ОС (т.к. △ ВОС – р/б) Значит, △АВО = △АОС (по трем сторонам), следовательно, Значит, ВК=КС, АК┴ВС, что и требовалось доказать.
| Один ученик у доски остальные в тетрадях.
Один ученик у доски остальные в тетрадях.
Один ученик у доски остальные в тетрадях.
Письменно в тетрадях | Р: проговаривать последовательность действий К: уметь письменно оформлять свои мысли | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7. Рефлексия | | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Сколько прямых можно провести через любые две точки? Как могут располагаться две прямые? С какими символами вы сегодня познакомились? Определите свое настроение в конце урока. | Поднимают руки. | Р: уметь оценивать правильность выполнения действий | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Постановка Д/З | | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Домашнее задание: п. 32; решить задачи № 242, 244 + следствия с доказательством | Слушают, записывают. |
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
4

 Получите свидетельство
Получите свидетельство Вход
Вход




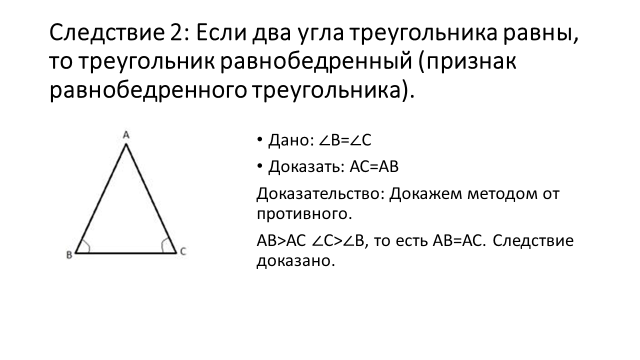 Обсудим следствие 2. Треугольник называется равнобедренным, если его две стороны равны. Из этого вытекает его свойство: углы при основании равны. А теперь у нас есть признак, что если углы при какой-либо стороне равны, то треугольник равнобедренный. Мы имеем признак равнобедренного треугольника.
Обсудим следствие 2. Треугольник называется равнобедренным, если его две стороны равны. Из этого вытекает его свойство: углы при основании равны. А теперь у нас есть признак, что если углы при какой-либо стороне равны, то треугольник равнобедренный. Мы имеем признак равнобедренного треугольника.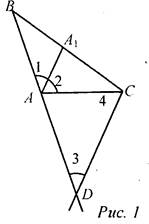
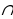 СО=О.
СО=О.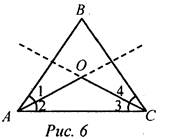

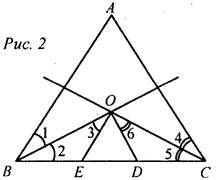
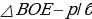 (по признаку р/б треугольника), значит BE = ОЕ.
(по признаку р/б треугольника), значит BE = ОЕ.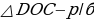 (по признаку р/б треугольника), значит CD = OD.
(по признаку р/б треугольника), значит CD = OD.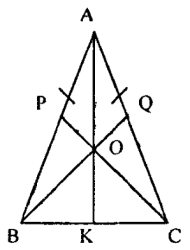
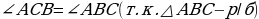
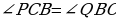 (по свойству равных треугольников).
(по свойству равных треугольников).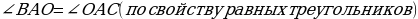 . Значит, АО – биссектриса
. Значит, АО – биссектриса 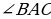 , а, следовательно АО – медиана и высота (по свойству биссектрисы, проведенной к основанию р/б треугольника).
, а, следовательно АО – медиана и высота (по свойству биссектрисы, проведенной к основанию р/б треугольника). 








 Аксиома параллельных прямых. (433.16 KB)
Аксиома параллельных прямых. (433.16 KB)
 0
0 31
31 0
0 Нравится
0
Нравится
0





