Тангенс, котангенс

Вопросы занятия:

·     познакомиться с понятиями тангенса и котангенса;

·     узнать, как понятия тангенса и котангенса связаны с координатами точек числовой окружности;

·     узнать какие знаки имеют тангенс и котангенс в зависимости от того, в какой четверти единичной окружности располагается точка.

Материал урока.

Прежде чем приступить к изучению темы, давайте вспомним определения синуса и косинуса.

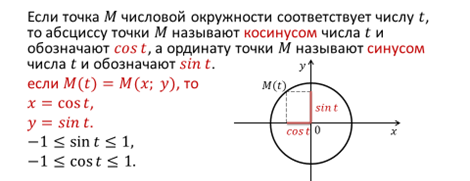
Рассмотрим пример.

Пример.

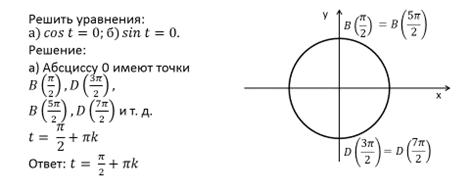
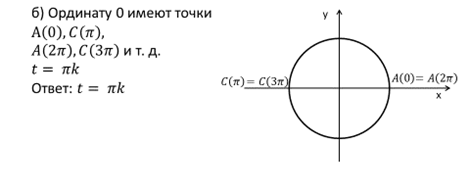
Определение.

Легко построить таблицу знаков тангенса и котангенса по четвертям окружности.

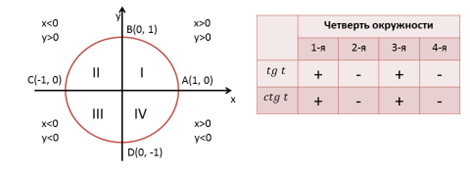
Зная таблицы основных значений синуса и косинуса, легко построить таблицу основных значений тангенса и котангенса. Достаточно разделить соответствующие значения синуса и косинуса друг на друга. В итоге получим следующую таблицу основных значений тангенса и котангенса.

Для тангенса и котангенса выполняются свойства, аналогичные тем, что были сформулированы для синуса и косинуса.

Свойство 1. Для любого t справедливы равенства:

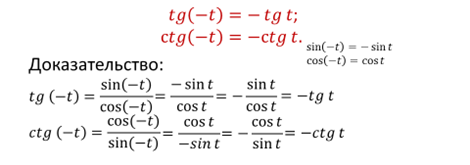
Свойство 2. Для любого t справедливы равенства:

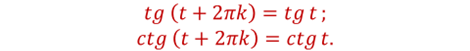
Свойство 3. Для любого t справедливы равенства:

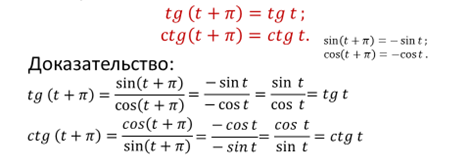
Для синуса и косинуса у нас есть геометрическая иллюстрация на числовой окружности. Можно дать и геометрическую иллюстрацию для тангенса.

Геометрическая иллюстрация для котангенса:

Решим несколько примеров.

Пример.

Пример.