Вопросы занятия:
· познакомиться с понятиями синуса и косинуса;
· узнать, как понятия синуса и косинуса связаны с координатами точек числовой окружности;
· узнать какие знаки имеют синус и косинус в зависимости от того, в какой четверти единичной окружности располагается точка.
Материал урока.
Прежде чем приступить к изучению новой темы, решите устно.
Упражнение.
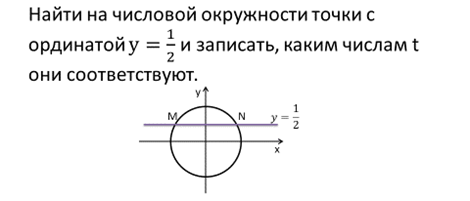
Определение.
Если точка M числовой окружности соответствует числу t, то абсциссу точки M называют косинусом числа t и обозначают cos t, а ординату точки M называют синусом числа t и обозначают sin t.
Итак, если M(t)=M(x; y), то x=cos t, y=sin t.
Поскольку радиус окружности равен 1, то, очевидно, что
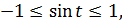
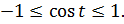
Мы знаем, что каждая точка числовой окружности имеет в системе XOY свои координаты, поэтому можем легко можем составить таблицу знаков синуса и косинуса по четвертям окружности.
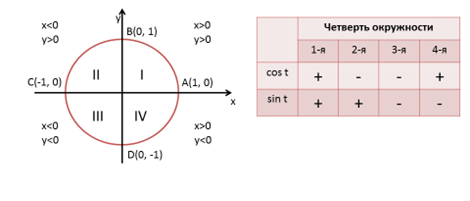
Уравнение числовой окружности имеет вид x2 + y2 = 1, применив формулы x=cos t, y=sin t, получим важное равенство, связывающее sin t и cos t:
cos2t + sin2t = 1.
Вернёмся к нашим основным макетам.
Зная таблицу координат основных точек первого макета легко записать таблицу значений синуса и косинуса для основных точек первого макета, для этого достаточно вместо букв x и y записать соответственно cos t и sin t.
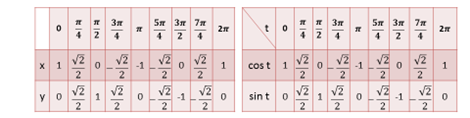
Аналогично, запишем таблицу значений синуса и косинуса для основных точек второго макета.
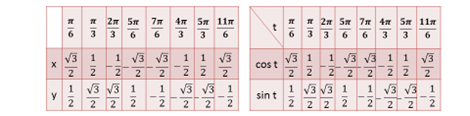
Рассмотрим пример.
Пример.
`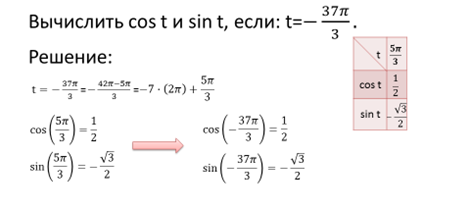
Сформулируем и докажем некоторые свойства синуса и косинуса.
Свойство 1. Для любого значения t справедливы равенства:
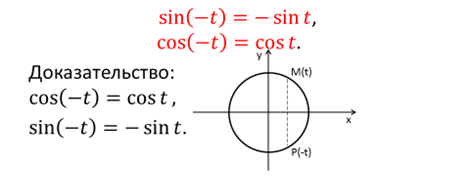
Свойство 2. Для любого значения t справедливы равенства:
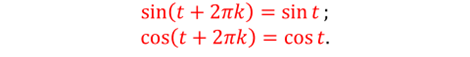
Свойство 3. Для любого значения t справедливы равенства:
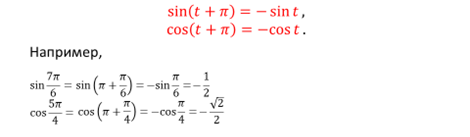
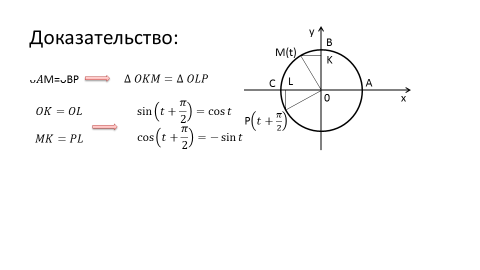
Доказательство.
Если числу t соответствует точка M числовой окружности, то числу t+π соответствует точка P, симметричная точке M относительно центра окружности – начала координат. У таких точек абсциссы равны по модулю, но противоположны по знаку; то же самое можно сказать и про ординаты точек. Это значит, что:
sin (t + π) = - sin t
cos (t + π) = - cos t
Сформулируем четвёртое свойство.
Свойство 4. Для любого значения t справедливы равенства:
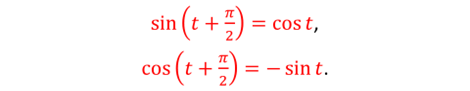
Рассмотрим пример.
Пример.
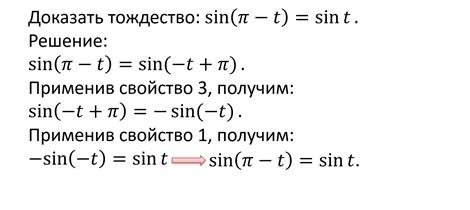

 Получите свидетельство
Получите свидетельство Вход
Вход



 1
1 4316
4316



Огромное спасибо! Очень удобно.