Получите свидетельство
Вход
Вопросы занятия:
· показать еще один способ решения систем линейных уравнений – способ сложения.
Материал урока
Мы с вами уже познакомились с двумя способами решения систем линейных уравнений с двумя переменными, а именно, с графическим способом и способом подстановки.
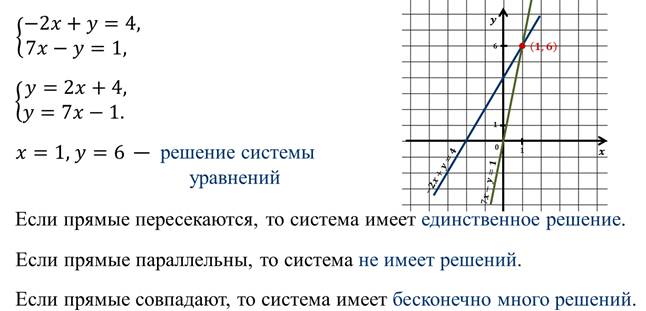
На этом уроке мы познакомимся с ещё одним способом решения систем линейных уравнений, который называют способом сложения.
Рассмотрим следующую систему
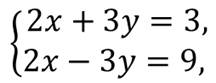
Обратите внимание, что в уравнениях системы коэффициенты при переменной игрек – противоположные числа. Сложим почленно левые и правые части уравнений
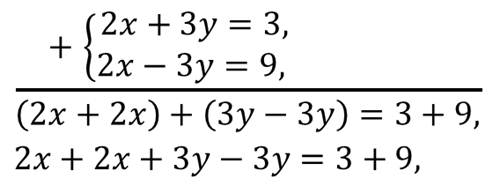
Приведём подобные слагаемые в обеих частях получившегося уравнения
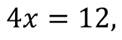
Видим, что получили уравнение с одной переменной.
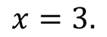
Затем, чтобы найти значение переменной игрек, мы подставим х = 3 в любое уравнение системы, например, в первое. Снова получили уравнение с одной переменной у. Решим его.
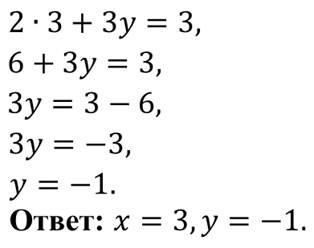
Убедиться в этом вы можете, подставив эти значения в каждое уравнение системы.
Пример.
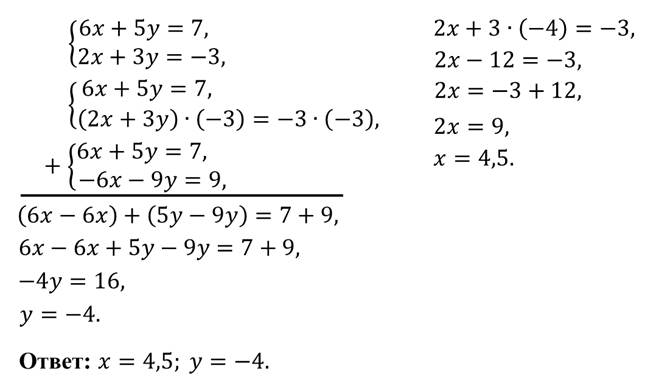
Пример.
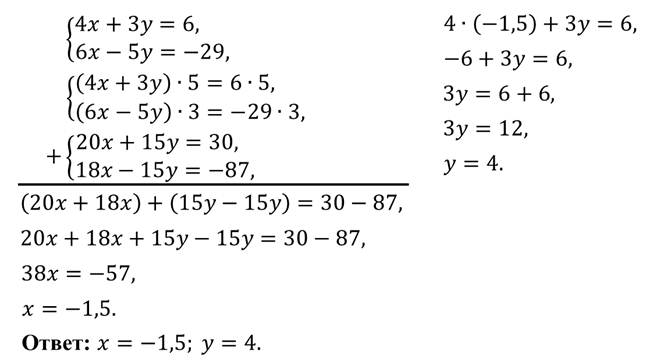
Пример.
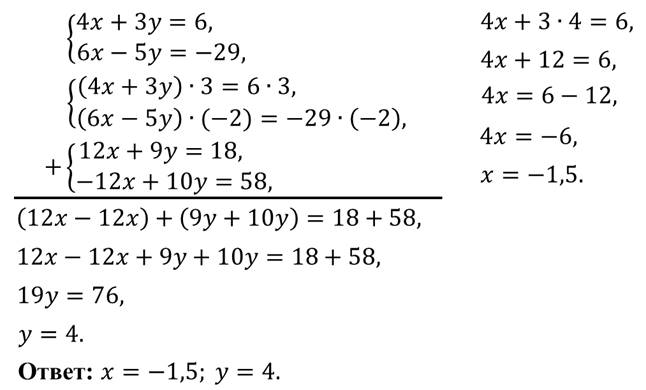
Можем сделать вывод: чтобы решить систему линейных уравнений способом сложения, надо:
1) умножить почленно уравнения системы, подбирая множители так, чтобы коэффициенты при одной из переменных стали противоположными числами;
2) сложить почленно левые и правые части уравнений системы;
3) решить получившееся уравнение с одной переменной;
4) найти соответствующее значение второй переменной.
При этом следует помнить, что если коэффициенты при одной из переменных являются противоположными числами, то решение системы сразу начинают с почленного сложения уравнений.
0
14053
