Решение систем линейных уравнений способом подстановки

Вопросы занятия:

·  показать еще один способ решения систем линейных уравнений – способ подстановки.

Материал урока

На прошлом уроке мы с вами говорили о системе линейных уравнений с двумя переменными.

Нам уже знаком графический способ решения систем линейных уравнений.

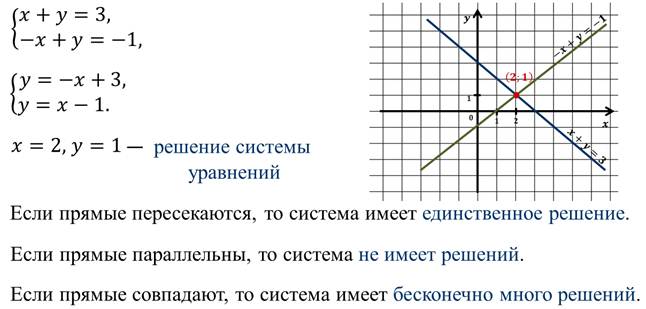
Мы также отмечали, что графический способ чаще всего позволяет находить решения лишь приближённо.

Сегодня на уроке мы познакомимся с ещё одним способом решения систем линейных уравнений с двумя переменными, который называют способом подстановки.

Итак, рассмотрим следующую систему

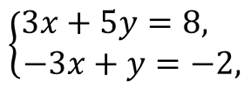
Заметим, что во втором уравнении системы коэффициент при у равен 1, поэтому мы легко можем выразить переменную у через переменную х.

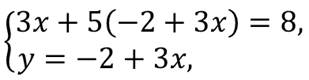
Далее мы подставим вместо у в первое уравнение системы это выражение и получим уравнение с одной переменной х.

Решим это уравнение.

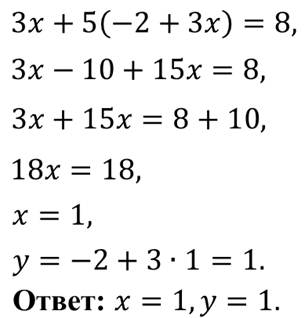
Вот так мы с вами решили систему уравнений способом подстановки.

Таким образом, чтобы решить систему уравнений способом подстановки, надо:

1.  выразить из какого-нибудь уравнения системы одну переменную через другую;

2.  подставить вместо этой переменной полученное выражение в другое уравнение системы;

3.  решить получившееся уравнение с одной переменной;

4.  найти соответствующее значение второй переменной.

Ранее мы с вами говорили о равносильных уравнениях, то есть уравнениях, которые имеют одни и те же корни.

То же самое можно сказать и о системах уравнений.

Определение.

Системы уравнений с двумя переменными, имеющие одни и те же решения, называются равносильными.

Системы, которые не имеют решений, также являются равносильными.

Ну а теперь давайте решим несколько систем рассмотренным выше способом.

Пример.

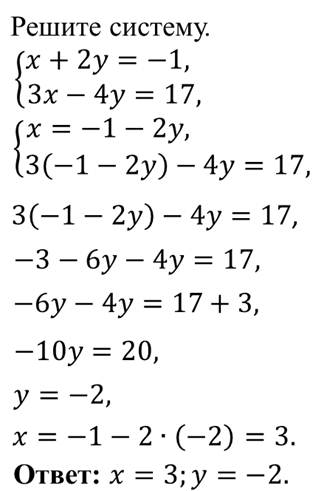
Пример.

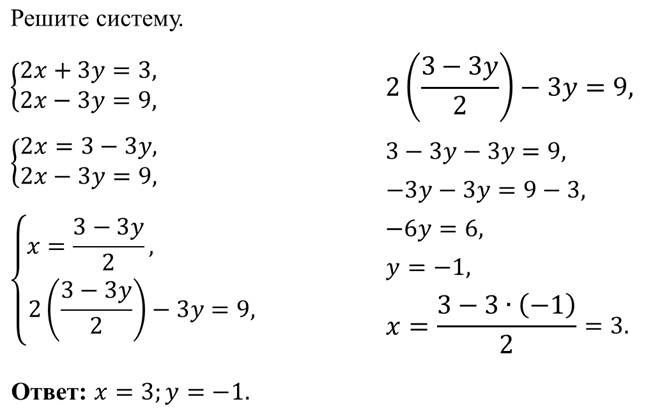
Итоги урока

На этом уроке мы рассмотрели алгоритм решения систем линейных уравнений способом подстановки и научились решать системы этим способом.