Вопросы занятия:
· ввести понятие «система линейных уравнений»;
· рассмотреть графический способ решения систем линейных уравнений.
Материал урока
Прежде, чем приступить к рассмотрению новой темы вспомним, что:

А теперь давайте рассмотрим задачу. Сумма двух чисел равна 25, а их разность – 17. Чему равны эти числа?
Пусть икс – первое число, а игрек – второе.
Так как по условию задачи сумма этих чисел равна 25, то можно составить уравнение:

Также известно, что разность чисел равна 17, а тогда можем записать следующее уравнение:

Таким образом, мы получили два уравнения с двумя переменными.
Чтобы ответить на вопрос задачи, нам надо найти такие значения переменных x и y, которые обращают каждое из уравнений в верное равенство, то есть найти общие решения уравнений.
Говорят, что требуется решить систему уравнений и записывают вот таким образом:

Теперь подбором найдём пару значений переменных:

Действительно, эта пара является решением каждого уравнения системы, так при подстановке этих значений мы получаем верные равенства.
Такая пара чисел называется решением системы.
Сформулируем определение.
Определение.
Решением системы уравнений с двумя переменными называется пара значений переменных, которая обращает каждое уравнение системы в верное равенство.
Решить систему уравнений – значит найти все её решения или доказать, что их нет.
Существует несколько способов решения систем уравнений с двумя переменными. И сейчас мы познакомимся с одним из них.
Возьмём следующую систему

Вам уже известно, как строить график линейного уравнения с двумя переменными. Давайте построим график каждого уравнения нашей системы.
Из каждого уравнения системы выразим переменную у через переменную х.

Так как графиком каждого из уравнений будет прямая, то для его построения нам достаточно указать две точки.

Отметим эти точки на координатной плоскости и проведём через них линии.

Обратите внимание, что построенные графики пересекаются в точке:

Координаты этой точки удовлетворяют обоим уравнениям, то есть являются решением системы уравнений. В этом можете убедиться самостоятельно, подставив эти значения в уравнения системы.
Таким образом, система имеет единственное решение:

Такой способ решения системы называется графическим.
Возникает вопрос: всегда ли система уравнений с двумя переменными имеет решения и если имеет, то сколько?
На примере мы с вами увидели, что если прямые (то есть графики уравнений) пересекаются, то система имеет единственное решение. А вот если прямые параллельны, то система не имеет решений. Если же прямые совпадают, то система имеет бесконечно много решений.
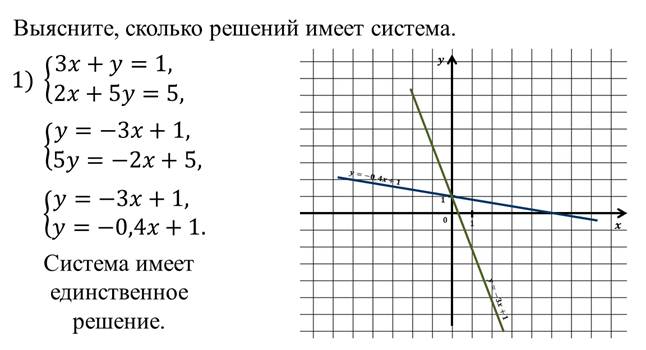
Рассмотрим пример, в котором надо выяснить, сколько решений имеет система.
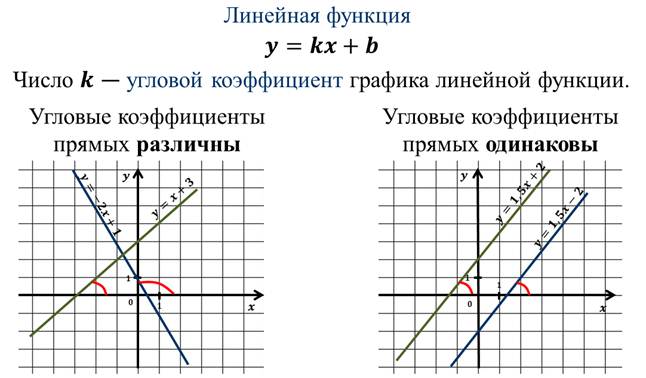
Но сначала вспомним, что:
Пример.
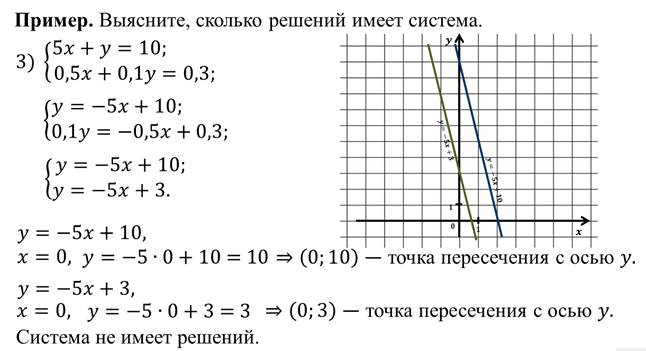
Пример.

Пример.
Итоги урока
Итак, сегодня на уроке мы рассмотрели одни из способов решения систем линейных уравнений с двумя переменными. Но следует отметить, что графический способ позволяет чаще всего находить решения лишь приближённо.

 Получите свидетельство
Получите свидетельство Вход
Вход




 1
1 10075
10075


1. урок 41.