На прошлом уроке мы с вами говорили, что параллелограмм – это четырёхугольник, у которого противоположные стороны попарно параллельны. Также мы рассмотрели некоторые свойства параллелограмма. Вспомним их.
Свойство 1.
Сумма углов при соседних вершинах параллелограмма равна 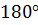 .
.

Свойство 2. Диагональ разбивает параллелограмм на два равных треугольника.
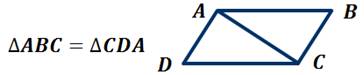
Свойство 3. У параллелограмма противоположные стороны равны.

Свойство 4. У параллелограмма противоположные углы равны.

Свойство 5. Диагонали параллелограмма точкой пересечения делятся пополам.

На этом уроке мы рассмотрим три признака параллелограмма. Отметим, что свойство – это то, чем обладает данная фигура. А признак – это то, чем фигура отличается от других, то есть черты, по которым мы можем отличить данную фигуру от других.
Теорема. 1-й признак параллелограмма. Если у четырёхугольника две стороны равны и параллельны, то этот четырёхугольник – параллелограмм.
Докажем это.
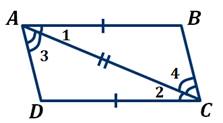
Рассмотрим 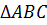 и
и
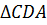 .
.
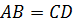 ,
,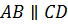 .
.
Сторона 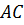 –
общая,
–
общая,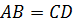 по
условию,
по
условию,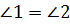 как
накр. лежащие при
как
накр. лежащие при 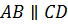 и
секущей
и
секущей 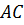 .
.
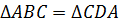 по
первому признаку. Следовательно,
по
первому признаку. Следовательно, 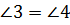 .
.
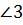 ,
,
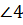 –
накр. лежащие при
–
накр. лежащие при 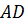 и
и
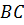 и
секущей
и
секущей 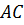 .
.
Так как 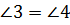 ,
то
,
то 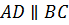 .
.
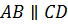 ,
,
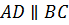 ,следовательно,
,следовательно,
 –
параллелограмм.
–
параллелограмм.
Теорема доказана.
Теорема. 2-й признак. Если в четырёхугольнике противоположные стороны равны, то этот четырёхугольник – параллелограмм.
Доказательство.
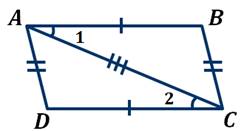
Пусть в четырёхугольнике ABCD
сторона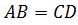 ,
,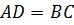 .
.
Проведём диагональ AC, которая разделяет четырёхугольник на два треугольника ABC и CDA.
Рассмотрим 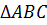 и
и
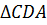 .
.
Сторона 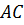 –
общая,
–
общая,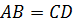 по
условию,
по
условию,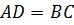 по
условию.
по
условию.
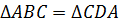 по
третьему признаку.
по
третьему признаку.
Следовательно, 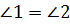 .
.
Так как 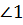 ,
,
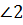 –
накр. лежащие при
–
накр. лежащие при 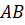 и
и
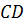 и
секущей
и
секущей 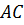 ,то
,то
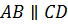 .
.
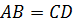 ,
,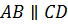 ,тогда
по 1-му признаку
,тогда
по 1-му признаку 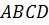 –
параллелограмм.
–
параллелограмм.
Теорема доказана.
Теорема. 3-й признак. Если у четырёхугольника диагонали пересекаются и точкой пересечения делятся пополам, то этот четырёхугольник – параллелограмм.
Доказательство.
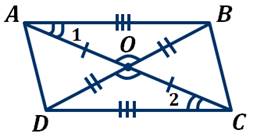
Пусть в четырёхугольнике ABCD диагонали AC и BD пересекаются в точке О и делятся этой точкой пополам.
Рассмотрим 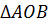 и
и
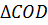 .
.
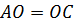 по
условию,
по
условию,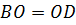 по
условию,
по
условию,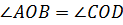 как
вертикальные.
как
вертикальные.
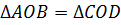 по
первому признаку.
по
первому признаку.
Следовательно, 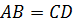 ,
,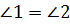 .Так
как
.Так
как 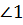 ,
,
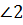 –
накр. лежащие при
–
накр. лежащие при 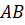 и
и
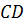 и
секущей
и
секущей 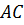 ,то
,то
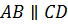 .
.
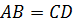 ,
,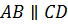 ,тогда
по 1-му признаку
,тогда
по 1-му признаку 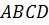 –
параллелограмм.
–
параллелограмм.
Теорема доказана.
Теперь решим несколько задач.
Задача. Докажите, что
четырёхугольник 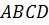 является
параллелограммом, если
является
параллелограммом, если 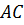 –
диагональ, а
–
диагональ, а 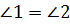 и
и
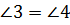 .
.
Доказательство.
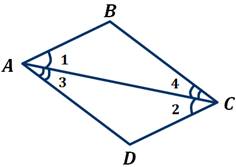
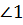 ,
,
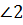 –
накр. лежащие при
–
накр. лежащие при 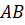 и
и
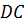 и
секущей
и
секущей 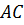 .
.
Так как 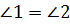 ,
то
,
то 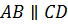 .
.
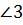 ,
,
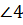 –
накр. лежащие при
–
накр. лежащие при 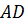 и
и
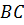 и
секущей
и
секущей 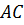 .
.
Так как 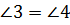 ,
то
,
то 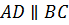 .
.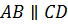 ,
,
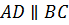 ,следовательно,
,следовательно,
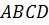 –
параллелограмм.
–
параллелограмм.
Решим эту задачу ещё одним способом.
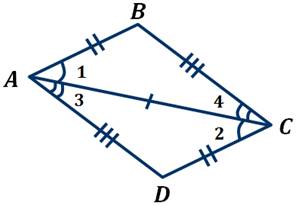
Рассмотрим 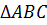 и
и
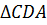 .Сторона
.Сторона
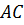 –
общая,
–
общая,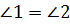 ,
,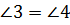 по
условию.
по
условию.
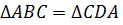 по
второму признаку, следовательно,
по
второму признаку, следовательно, 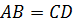 ,
,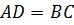 .
.
Тогда 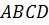 –
параллелограмм по 2-му признаку.
–
параллелограмм по 2-му признаку.
Что и требовалось доказать.
Задача. Отрезки 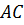 и
и
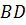 –
диагонали четырёхугольника
–
диагонали четырёхугольника 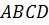 ,
которые пересекаются в точке
,
которые пересекаются в точке 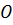 .
.
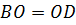 ,
а
,
а 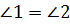 .
Докажите, что четырёхугольник
.
Докажите, что четырёхугольник 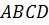 –
параллелограмм.
–
параллелограмм.
Доказательство.
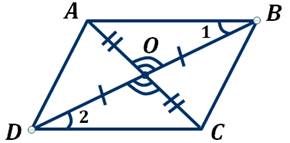
Рассмотрим 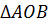 и
и
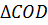 .
.
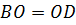 по
условию,
по
условию,
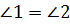 по
условию,
по
условию,
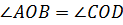 как
вертикальные.
как
вертикальные.
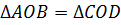 по
второму признаку.
по
второму признаку.
Следовательно, 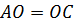 .
.
Тогда 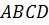 –
параллелограмм по 3-му признаку.
–
параллелограмм по 3-му признаку.
Что и требовалось доказать.

 Получите свидетельство
Получите свидетельство Вход
Вход



 0
0 21905
21905