Сегодня на уроке мы познакомимся с геометрической фигурой, которую называют трапецией.
Итак, трапецией называется четырёхугольник, у которого две стороны параллельны, а две другие – нет.

Параллельные стороны трапеции называются основаниями. А не параллельные – боковыми сторонами.
Перпендикуляр, проведённый из любой точки одного из оснований на другое основание или его продолжение, называется высотой трапеции.
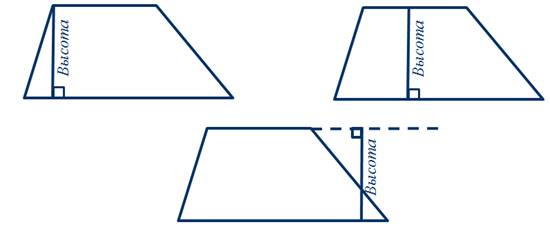
Трапеция, у которой есть прямой угол, называется прямоугольной. Следует отметить, что, так как основания AB и CD параллельны, прямая BC – секущая, а сумма односторонних углов равна 180º, то и угол BCD также равен 90º.
Трапеция, у которой боковые стороны равны, называется равнобедренной.
Далее мы рассмотрим некоторые свойства и признаки равнобедренной трапеции.
Теорема. Свойство углов равнобедренной трапеции. Углы при основании равнобедренной трапеции равны.
Доказательство.

Рассмотрим прямоугольные 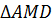 и
и 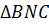 .
.
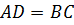 , так как
, так как 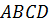 – равнобедр.
трапеция,
– равнобедр.
трапеция,
 .
.
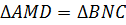 по катету и
гипотенузе.
по катету и
гипотенузе.
Следовательно,  .
.
Теорема доказана.
Теорема. Свойство диагоналей равнобедренной трапеции. Диагонали равнобедренной трапеции равны.
Доказательство.

Рассмотрим  и
и  .
.
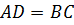 , так как
, так как 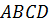 – равнобедр.
трапеция,сторона
– равнобедр.
трапеция,сторона 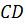 – общая,
– общая,
 как углы при
основании равнобедр. трапеции.
как углы при
основании равнобедр. трапеции.
 по первому
признаку.
по первому
признаку.
Следовательно,  .
.
Теорема доказана.
Теорема. Признак равнобедренной трапеции. Если у трапеции углы при основании равны, то она равнобедренная.
Доказательство.

Рассмотрим прямоугольные 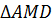 и
и 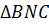 .
.
 по условию.
по условию.
 .
.
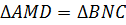 по катету и
противолежащемуострому углу.
по катету и
противолежащемуострому углу.
Следовательно, 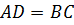 .
.
Тогда трапеция 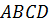 –
равнобедренная.
–
равнобедренная.
Теорема доказана.
Теорема. Признак равнобедренной трапеции. Если у трапеции диагонали равны, то она равнобедренная.
Доказательство.

Рассмотрим прямоугольные  и
и  .
.
 по условию,
по условию, .
.
 по катету и гипотенузе.
по катету и гипотенузе.
Следовательно,  .
.
Рассмотрим  и
и  .
.
 по
условию,сторона
по
условию,сторона 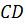 – общая,
– общая, .
.
 по первому
признаку.
по первому
признаку.
Следовательно, 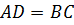 .
.
Тогда трапеция 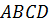 –
равнобедренная.
–
равнобедренная.
Теорема доказана.
А теперь решим несколько задач.
Задача. 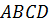 – трапеция, у
которой
– трапеция, у
которой 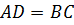 .
. 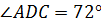 . Найдите
градусную меру
. Найдите
градусную меру  .
.
Решение.

Так как 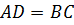 , то трапеция
, то трапеция 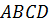 –
равнобедренная.
–
равнобедренная.
 как углы при
основании равнобедр. трапеции.
как углы при
основании равнобедр. трапеции.
 ,
,  –
внутр. односторонние при
–
внутр. односторонние при  и секущей
и секущей 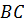 , то есть
, то есть
 ,
,
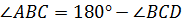 ,
,
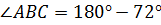 ,
,
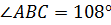 .
.
Ответ:  .
.
Задача. В прямоугольной
трапеции 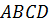 проведена
диагональ
проведена
диагональ  .
.  ,
,  . Найдите
градусную меру
. Найдите
градусную меру  .
.
Решение.

 как накр.
лежащие при
как накр.
лежащие при  и секущей
и секущей  ,то есть
,то есть 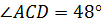 .
.
 ,следовательно,
,следовательно,  –
равнобедренный, тогда
–
равнобедренный, тогда  .
.
Для  :
:  ,
,
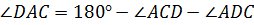 ,
,
 ,
,
 .
.
Ответ: 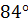 .
.

 Получите свидетельство
Получите свидетельство Вход
Вход



 0
0 18675
18675

