С понятием квадратного корня из числа а вы уже знакомы: это такое число, квадрат которого равен а.
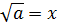 ,
,
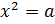 ,
,
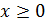 ,
,
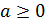
Аналогично
определяется корень 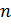 -й
степени из числа а, где
-й
степени из числа а, где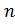 –
произвольное натуральное число.
–
произвольное натуральное число.
А теперь давайте решим такое уравнение:
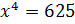
Итак,
это уравнение мы можем переписать в таком виде: 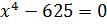 .
Или
.
Или 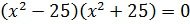 .
.
Тогда
наше уравнение равносильно совокупности уравнений: 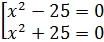 .
.
Понятно,
что уравнение 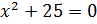 не
имеет решения на множестве действительных чисел. Значит, остаётся решить
уравнение
не
имеет решения на множестве действительных чисел. Значит, остаётся решить
уравнение
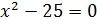
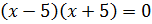
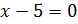
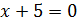
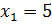
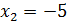
Итак,
наше уравнение 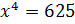 имеет
два действительных корня 5 и –5. Их называют корнями четвёртой степени
из числа 625. В свою очередь,
положительный корень (число 5) называют арифметическим корнем четвёртой
степени из числа 625. Обозначают его так:
имеет
два действительных корня 5 и –5. Их называют корнями четвёртой степени
из числа 625. В свою очередь,
положительный корень (число 5) называют арифметическим корнем четвёртой
степени из числа 625. Обозначают его так: 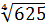 .
Таким образом,
.
Таким образом, 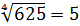 .
.
Запомните! Арифметическим
корнем натуральной степени 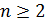 из
неотрицательного числа а называется неотрицательное число,
из
неотрицательного числа а называется неотрицательное число, 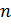 -я
степень которого равна а.
-я
степень которого равна а.
Арифметический
корень 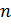 -ой
степени из числа а обозначают так:
-ой
степени из числа а обозначают так: 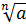 .
Символ
.
Символ 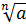 называют
знаком арифметического квадратного корня или радикалом
(от латинского слова «радикс» – корень), число
называют
знаком арифметического квадратного корня или радикалом
(от латинского слова «радикс» – корень), число 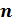 называется
показателем корня, а число а, стоящее под знаком
корня, – подкоренным выражением.
называется
показателем корня, а число а, стоящее под знаком
корня, – подкоренным выражением.
Вам
хорошо известен такой частный случай арифметического корня 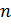 -й
степени, как корень второй степени, или квадратный корень из числа, то
есть когда
-й
степени, как корень второй степени, или квадратный корень из числа, то
есть когда 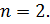
В
этом случае показатель корня не пишут, а пишут просто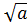 .
.
Ещё
одним частным случаем является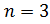
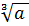 мы
привыкли называть его корнем кубическим.
мы
привыкли называть его корнем кубическим.
Как
правило, когда ясно, что речь идёт об арифметическом корне 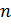 -й
степени, слово «арифметический» не произносят, а говорят кратко: «корень
энной степени».
-й
степени, слово «арифметический» не произносят, а говорят кратко: «корень
энной степени».
Действие,
посредством которого отыскивается корень 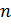 -й
степени, называется извлечением корня
-й
степени, называется извлечением корня 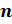 -й степени.
Это действие является обратным действию возведения в
-й степени.
Это действие является обратным действию возведения в 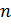 -й
степень.
-й
степень.
Равенство
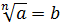 при
при
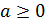 верно,
когда выполняются два условия:
верно,
когда выполняются два условия: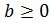 ;
второе —
;
второе —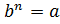 .
.
Например,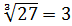 .
.
Число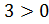 ;
;
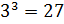 .
.
Видим,
что оба условия выполняются. Значит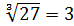 верно.
верно.
Из
определения арифметического корня следует, что если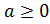 ,
то
,
то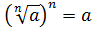 .
.
Например,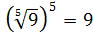
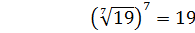
А
теперь давайте решим следующие уравнения: 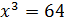 и
и
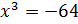 .
Итак, первое уравнение
.
Итак, первое уравнение
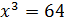
Перепишем
это уравнение в виде: 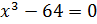 .
.
Преобразуем
наше уравнение, применяя формулу разности кубов. Имеем:
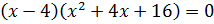
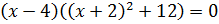
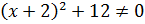
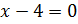
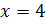
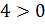
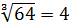
Перейдём к уравнению 2:
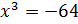
Перепишем
это уравнение в виде: 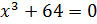 .
.
Преобразуем наше уравнение, применяя
формулу разности кубов. Имеем: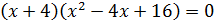 .
.
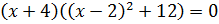
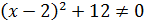
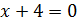
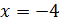
Так
как 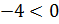 ,
то число –4 является корнем из числа –64. Однако это число не является
арифметическим корнем по определению. Число
,
то число –4 является корнем из числа –64. Однако это число не является
арифметическим корнем по определению. Число 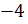 называют
корнем кубическим из числа
называют
корнем кубическим из числа 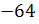 и
обозначают так:
и
обозначают так: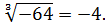
Вообще,
для любого нечётного натурального числа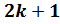 ,
уравнение
,
уравнение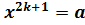 ,
при
,
при 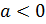 имеет
только один корень, причём отрицательный. Этот корень обозначается, как и
арифметический корень, символом
имеет
только один корень, причём отрицательный. Этот корень обозначается, как и
арифметический корень, символом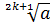 .
.
И называют его корнем нечётной степени из отрицательного числа.
Запомните!
При нечётном 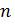 существует
существует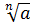 ,
и притом только один. Для корней нечётной степени справедливо равенство
,
и притом только один. Для корней нечётной степени справедливо равенство 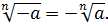
Например,
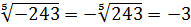
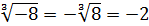
Корень
нечётной степени из отрицательного числа а связан с арифметическим корнем из
числа 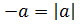 следующим
равенством:
следующим
равенством: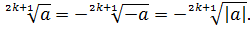
Например,
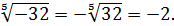
Арифметический
корень 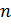 -й
степени обладает несколькими свойствами. Перечислим их. Итак, при условии, что
-й
степени обладает несколькими свойствами. Перечислим их. Итак, при условии, что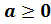 ,
,
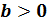 ,
а
,
а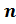 ,
,
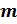 и
и
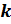 –
натуральные числа, причём
–
натуральные числа, причём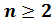 ,
,
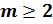 ,
справедливы равенства:
,
справедливы равенства:
1.
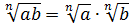 .
.
2.
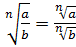 .
.
3.
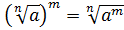 .
.
4.
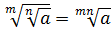 .
.
5.
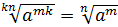 .
.
Обратите
внимание, что в первом свойстве число 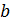 может
также быть равным
может
также быть равным 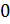 ;
в третьем свойстве число
;
в третьем свойстве число 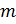 может
быть любым целым, если
может
быть любым целым, если 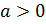 .
.
Докажем справедливость этих свойств. Итак, первое свойство.
1.
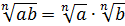 .
.
По
определению арифметического корня 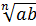 –
это такое неотрицательное число,
–
это такое неотрицательное число, 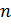 -я
степень которого равна произведению
-я
степень которого равна произведению 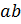 .
.
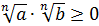 ;
;
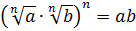 .
.
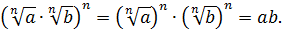
2.
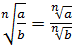 .
.
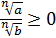 ;
;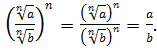
3.
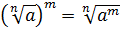 .
.
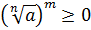 ;
;
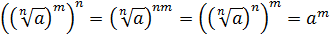 .
.
4.
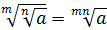 .
.
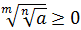 ;
;
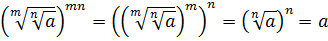 .
.
5.
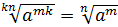 .
.
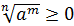 ;
;
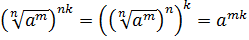 .
.
А теперь давайте приступим к практической части нашего урока.
Задание
1.
Найдите значения выражений а) 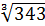 ;
б)
;
б) 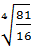 ;
в)
;
в) 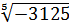 .
.
Решение.
а)
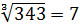 ;
б)
;
б) 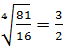 ;
в)
;
в) 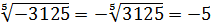 .
.
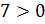 ;
;
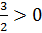 ;
;
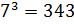 ;
;
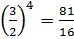 ;
;
Задание
2.
Преобразуйте выражения: а) 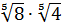 ;
б)
;
б) 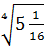 ;
в)
;
в) 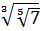 ;
г)
;
г) 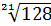 .
.
Решение.
а)
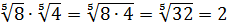 ;
;
б)
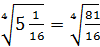
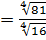
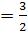 ;
;
в)
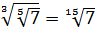 ;
;
г)
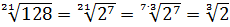 .
.

 Получите свидетельство
Получите свидетельство Вход
Вход



 0
0 18544
18544

