Напомним,
что геометрическая прогрессия – это числовая
последовательность ,
,
 ,
,
 ,
…,
,
…,  ,
…, где
,
…, где ,
что для всех натуральных
,
что для всех натуральных  выполняется
равенство
выполняется
равенство ,
где
,
где  .
Число
.
Число  называется
знаменателем геометрической последовательности, число
называется
знаменателем геометрической последовательности, число  –первым
её членом, а число
–первым
её членом, а число –
общим её членом.
–
общим её членом.
 ,
,
 ,
,
 ,
,
 ,
…,
,
…,  ,
…
,
… ,
,
 ,
,  ,
,  ,
,  , …,
, …,  , …
, … ,
,
Также
напомним, что  -ый
член геометрической прогрессии можно вычислить по формуле
-ый
член геометрической прогрессии можно вычислить по формуле 
А
сумму первых  членов
геометрической прогрессии можно вычислить по формуле
членов
геометрической прогрессии можно вычислить по формуле  , если
, если  ;
;
 , если
, если  .
.
Однако среди геометрических прогрессий особый интерес вызывают так называемые бесконечно убывающие геометрические прогрессии. Давайте познакомимся с такими прогрессиями.
Начнём с примера. Итак, перед вами изображены квадраты.

Сторона
первого, самого большого квадрата равна  ,
сторона второго равна
,
сторона второго равна  ,
сторона третьего квадрата –
,
сторона третьего квадрата –  ,
сторона четвёртого квадрата –
,
сторона четвёртого квадрата –  ,
сторона пятого квадрата –
,
сторона пятого квадрата –  и
так далее.
и
так далее.
Обратите
внимание! Стороны наших квадратов образуют геометрическую прогрессию:
 ,
,  ,
,  ,
,  ,
,  , …
, …
Перепишем
эту геометрическую прогрессию в таком виде:  ,
,  ,
,  ,
,  ,
,  , …,
, …,  , …
, …
Знаменатель
этой геометрической прогрессии равен  .
.
Заметим, что и площади этих квадратов также образуют геометрическую прогрессию:
 ,
,
 ,
,
 ,
,
 ,
,
 ,
…
,
…
 ,
,
 ,
,
 ,
,
 ,
,
 ,
…,
,
…,  ,
…
,
…

Хотелось
бы отметить, что стороны квадратов и их площади с возрастанием номера  становятся
всё меньше и всё больше приближаются к
становятся
всё меньше и всё больше приближаются к .
Так вот, каждую из прогрессий, что мы с вами записали, называют бесконечно
убывающей геометрической прогрессией.
.
Так вот, каждую из прогрессий, что мы с вами записали, называют бесконечно
убывающей геометрической прогрессией.
А теперь давайте рассмотрим следующую геометрическую прогрессию:
 ,
,  ,
,  ,
,  , …,
, …,  , …
, …
Здесь ,
,  ,
,  ,
,  , … , знаменатель нашей
геометрической прогрессии
, … , знаменатель нашей
геометрической прогрессии  .
.
Видим,
что с возрастанием номера  члены
этой прогрессии приближаются к
члены
этой прогрессии приближаются к .
Значит, эта прогрессия является бесконечно убывающей геометрической
прогрессией. Обратите внимание!
.
Значит, эта прогрессия является бесконечно убывающей геометрической
прогрессией. Обратите внимание!  .
.
Запомните: геометрическая прогрессия называется бесконечно убывающей, если модуль её знаменателя меньше единицы.
А теперь давайте перейдём к выводу формулы суммы бесконечно убывающей геометрической прогрессии.

Итак,
на экране вы видите квадрат со стороной равной единице. Разделим этот квадрат
пополам. Заштрихуем обе части нашего квадрата, как показано на экране. Продолжим
делить пополам наши квадраты и штриховать их. Заметим, что площади
заштрихованных прямоугольников образуют бесконечно убывающую
геометрическую прогрессию:  ,
,  ,
,  ,
,  ,
,  , …
, …
Если
мы заштрихуем все получающиеся таким образом прямоугольники, то понятно, что
весь квадрат покроется штриховкой. Разумеется, сумма площадей всех
заштрихованных прямоугольников будет равна единице. То есть  …
…
Обратите внимание: в левой части нашего равенства стоит сумма бесконечного числа слагаемых.
Давайте
рассмотрим сумму первых  слагаемых.
Применяя формулу суммы
слагаемых.
Применяя формулу суммы  членов
геометрической прогрессии, имеем
членов
геометрической прогрессии, имеем  ….
Получим, что
….
Получим, что  .
.
Заметим,
что если  неограниченно
возрастает, то
неограниченно
возрастает, то  будет
как угодно близко приближаться к 0. Это выражение записывают следующим образом:
будет
как угодно близко приближаться к 0. Это выражение записывают следующим образом:
 при
при
 ,
а читают так: «единица делённая на два в степени эн стремится к нулю при эн
стремящемся к бесконечности, или предел единицы делённой на два в степени эн
при эн стремящемся к бесконечности равен нулю».
,
а читают так: «единица делённая на два в степени эн стремится к нулю при эн
стремящемся к бесконечности, или предел единицы делённой на два в степени эн
при эн стремящемся к бесконечности равен нулю».
Так
как  при
при
 ,
то
,
то  при
при
 ,
то есть
,
то есть  или
или
 .
Поэтому бесконечную сумму
.
Поэтому бесконечную сумму  …
… .
.
В
этом случае говорят, что сумма бесконечно убывающей геометрической прогрессии
есть предел последовательности  ,
,  ,
,  , …,
, …,  , …
, …
Например,
если мы возьмём бесконечно убывающую геометрическую прогрессию  ,
,  ,
,  ,
,  , …,
, …,  , …
, …
Где
 ,
, .
.
 ,
,
 ,
,
 ,
…,
,
…,
 ,
…
,
…
Так
как  ,
то
,
то  .
.
А теперь выведем формулу суммы бесконечно убывающей геометрической прогрессии.
Мы
помним, что сумму первых  членов
геометрической прогрессии можно вычислить по формуле
членов
геометрической прогрессии можно вычислить по формуле  .
.
Перепишем
эту формулу таким образом:  .
.
Так
как  ,
то
,
то  ,
, .
.
Следовательно,
 .
.
Таким
образом, сумму  бесконечно
убывающей геометрической прогрессии можно вычислить по формуле:
бесконечно
убывающей геометрической прогрессии можно вычислить по формуле:  .
.
Из
этой формулы при  имеем
имеем
 .
.
Это равенство обычно записывают следующим образом:
 …
… …
… .
.
Обратите
внимание: это равенство справедливо при  ,
в частности при
,
в частности при  .
.
Задание 1.
Докажите,
что геометрическая прогрессия:
 …
, является бесконечно убывающей.
…
, является бесконечно убывающей.
Решение.
 ,
,  .
.


Следовательно, данная геометрическая прогрессия является бесконечно убывающей.
Задание 2.
Найдите
сумму бесконечно убывающей геометрической прогрессии  …
…
Решение.
 ,
,
 .
.




Задание 3.
Найдите
сумму бесконечно убывающей геометрической прогрессии, если  ,
,  .
.
Решение.
По условию нам даны  и
и
 прогрессии.
прогрессии.
 ,
,
 .
.












 Получите свидетельство
Получите свидетельство Вход
Вход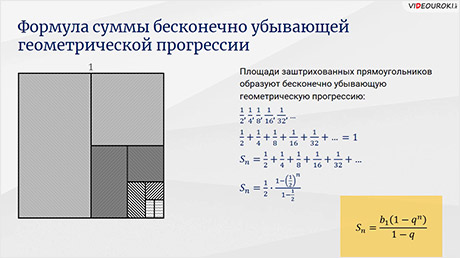



 0
0 19917
19917

