Вы уже знакомы с конечными, бесконечными периодическими десятичными дробями, которые являются рациональными числами.

Но в математике существуют и непериодические бесконечные десятичные дроби, которые не являются рациональными числами.
Например,
вот такое число:  … . Это число
является иррациональным.
… . Это число
является иррациональным.
Итак, иррациональным числом называется бесконечная десятичная непериодическая дробь.
Кстати, иррациональные числа, как и рациональные, могут быть как положительными, так и отрицательными. К примеру, следующие числа:

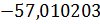
Первое число положительное иррациональное число, второе – отрицательное иррациональное число.
Числа
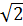 ,
,  ,
, 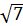 ,
,  ,
, ,
, являются иррациональными
числами, так как эти числа можно представить в виде бесконечных
десятичных непериодических дробей.
являются иррациональными
числами, так как эти числа можно представить в виде бесконечных
десятичных непериодических дробей.
С понятием иррациональных чисел мы с вами разобрались. Теперь давайте перейдём к действиям с ними. И ответим на такой вопрос: какие же числа получают в результате выполнения арифметических действий с иррациональными числами?
При сложении, вычитании, умножении и делении иррациональных чисел результат может оказаться как рациональным, так и иррациональным числом.




Множество иррациональных
чисел принято обозначать заглавной латинской буквой  .
.
Рациональные и иррациональные числа вместе образуют множество действительных чисел.
Множество
действительных чисел принято обозначать заглавной латинской буквой  . Запись
. Запись  означает,
что
означает,
что  является
действительным числом.
является
действительным числом.
Действительным
числом называется бесконечная десятичная дробь, то есть  … или
… или  …, где
…, где  – целое
неотрицательное число, а каждая из букв
– целое
неотрицательное число, а каждая из букв  ,
,  ,
, 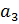 и так далее – это
одна из десяти цифр:
и так далее – это
одна из десяти цифр:  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
, 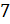 ,
,  ,
, 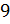 .
.
Например,
в записи числа  …
…
 ,
,  ,
,  ,
,  ,
,  ,
,  …
…
В
записи действительного числа  …
…
 ,
, 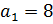 ,
, 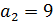 ,
,  ,
, ,
,  …
…
В
записи действительного числа  …
…
 ,
,  ,
,  ,
,  ,
, …
…
В
записи действительного числа  …
…
 ,
,  ,
,  ,
,  , при
, при  .
.
Действительные числа могут быть как положительными, так и отрицательными, а могут и равняться нулю.
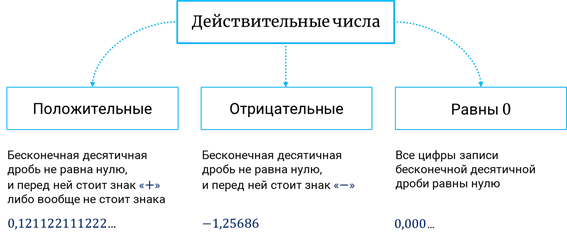
Если все цифры записи бесконечной десятичной дроби равны нулю, то и дробь равна нулю. А если бесконечная десятичная дробь не равна нулю и перед ней стоит знак «+» либо вообще не стоит знака, то это положительное действительное число. А если стоит знак «–», то это отрицательное действительное число.
Все основные действия и правила над рациональными числами, которые вы знаете, сохраняются и для действительных чисел. Например, переместительный, сочетательный и распределительный законы, правила сравнения, правила раскрытия скобок и так далее.
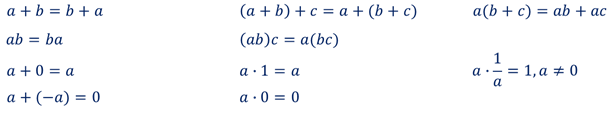
Только арифметические операции над действительными числами, как правило, заменяют операциями над их приближениями.
Например, давайте вычислим

 …
…
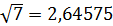 …
…
Если вычислять сумму этих корней с точностью до единицы, то
 .
.
Если вычислять эту же сумму, но с точностью до одной десятой, то
 .
.
А вот если вычислять сумму наших корней с точностью до одной сотой, то
 .
.
Обратите
внимание: ;
;  ;
;  и так далее
являются последовательными десятичными приближениями значения
и так далее
являются последовательными десятичными приближениями значения  .
Причём первые два числа с избытком, последнее с недостатком. Заметим, что при вычислении
.
Причём первые два числа с избытком, последнее с недостатком. Заметим, что при вычислении
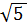 и корня из
и корня из 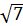 сами
числа
сами
числа  и корень
и корень 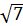 мы
заменяли на их приближения, то есть рациональными числами, а
затем выполняли сложение чисел по известным правилам.
мы
заменяли на их приближения, то есть рациональными числами, а
затем выполняли сложение чисел по известным правилам.
Так
же, как и для рациональных чисел, модуль действительного числа
обозначается и определяется так: 
Например,
 …
…
 …
…
И ещё нам с вами осталось дать геометрическое истолкование действительных чисел.
Итак, геометрически действительные числа изображаются точками числовой прямой. Множество действительных чисел «заполняет» всю числовую прямую. Причём каждому действительному числу соответствует единственная точка на числовой прямой. Верно и обратное утверждение: каждой точке числовой прямой соответствует единственное действительное число.
Точку,
изображающую действительное число  , также обозначают
буквой
, также обозначают
буквой  .
.

Отметим,
что если действительное число  меньше действительного
числа
меньше действительного
числа  , то на числовой
прямой точка
, то на числовой
прямой точка  будет
лежать левее точки
будет
лежать левее точки  .
.
А теперь давайте приступим к практической части нашего урока.
Задание
1.
Сравните числа  ,
,  и
и 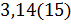 .
.
Решение.
 …
…
 …
…
 …
…
Видим: у данных чисел совпадают целые части и цифры десятых.
Значит
 ,
, .
.
Теперь
сравним  и
и  .
.
Видим: у этих чисел совпадают первые четыре цифры после запятой, а вот пятая цифра после запятой у значения.
Следовательно
Отсюда
получаем,
Задание
2.
Выясните, каким числом (рациональным или иррациональным) является числовое
значение выражения  .
.
Решение. Раскроем скобки в нашем выражении, применяя формулу квадрата суммы. Воспользуемся следствием из определения квадратного корня.
 .
.
Затем применим свойство корня из произведения. Приведём подобные.
Получим
 .
.
Данное
число является иррациональным, так как содержит иррациональное
число  .
.

 Получите свидетельство
Получите свидетельство Вход
Вход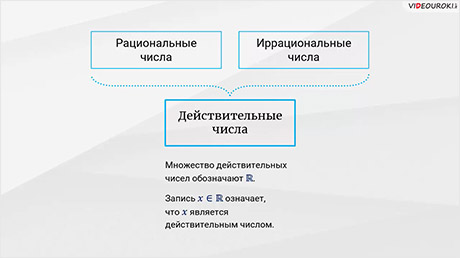



 0
0 12130
12130

