Целые и рациональные числа

Вы уже знаете, что числа, которые мы используем в счёте, называют натуральными. Кстати, натуральные числа – это один из первых математических объектов, который стал изучать человек, так как повседневная жизнь требовала использования натуральных чисел на практике, и в частности, в счёте.

Поэтому и изучение математики в школе мы начинали именно со знакомства с натуральными числами.

Итак, давайте перечислим натуральные числа: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 и так далее. Все натуральные числа образуют множество натуральных чисел, которое обозначают заглавной латинской буквой .

С понятием натуральных чисел мы с вами разобрались, а теперь давайте перейдём к действиям с ними. И ответим на вопрос: какие числа получают при сложении и умножении натуральных чисел?

Конечно же, вам не составит труда ответить на этот вопрос. И вы сразу скажете, что при сложении натуральных чисел всегда получают натуральные числа.

И при умножении натуральных чисел тоже всегда получают натуральные числа.

Тогда возникает новый вопрос: а какие числа мы получим при вычитании и делении натуральных чисел?

Так вот, при нахождении разности и частного натуральных чисел не всегда получаются натуральные числа.

В связи с этим математикам пришлось расширять знания, связанные с числами.

Если мы добавим к натуральным числам нуль и отрицательные числа (то есть числа, которые противоположны натуральным), то множество натуральных чисел расширится до множества целых чисел.

Множество целых чисел принято обозначать заглавной латинской буквой . Оно состоит из следующих элементов: .

Мы с вами разобрались с понятием целых чисел, а теперь давайте перейдём к действиям с ними. Понятно, что при сложении, вычитании и умножении целых чисел всегда получают целые числа.

Чего нельзя сказать о делении целых чисел. При нахождении частного двух целых чисел в результате не всегда получают целые числа.

(

Следовательно, понятия, связанные с числами, пришлось расширять дальше. Так, множество целых чисел расширили, введя множество рациональных чисел.

Итак, числа вида , где m – целое число, n – натуральное число, составляют множество рациональных чисел. Это множество принято обозначать заглавной латинской буквой . Кстати, любое целое число можно представить в виде рационального, например, число m можно представить в виде .

Множество рациональных чисел позволило находить частное любых двух целых чисел при условии, что делитель не равен нулю.

Кроме того, при выполнении всех четырёх арифметических действий (кроме деления на нуль) над рациональными числами всегда получают рациональные числа.

Рациональное число можно представить в виде дроби , где m – целое число, k – натуральное число. Если рациональное число можно представить в виде дроби , где m – целое число, k – натуральное число, то его можно записать в виде конечной десятичной дроби.

Заметим, что одно и то же рациональное число можно представить различными дробями, которые получаются из несократимой дроби умножением её числителя и знаменателя на одно и то же целое число, отличное от нуля.

Существуют и рациональные числа, которые нельзя записать в виде конечной десятичной дроби.

Если, например, мы попытаемся записать число  в виде десятичной дроби, используя алгоритм деления уголком, то получим бесконечную десятичную дробь ….

Напомним, что такую бесконечную десятичную дробь называют периодической, а повторяющуюся цифру 3 – её периодом. Нашу периодическую дробь … коротко записывают так: . А читают нашу периодическую дробь так: «нуль целых и три в периоде».

Тогда можем сделать такой вывод: любая периодическая дробь – это бесконечная десятичная дробь, у которой, начиная с некоторого десятичного знака, повторяется одна и та же цифра или группа цифр – период дроби.

Например, десятичная дробь …. Она равна . Это периодическая дробь с периодом 23. Читают эту дробь так: «пятнадцать целых семнадцать сотых и двадцать три в периоде».

Заметим, что каждое целое число или конечную десятичную дробь можно считать и бесконечной десятичной периодической дробью с периодом, равным нулю.

Вообще, любую конечную десятичную дробь можно записать в виде бесконечной дроби двумя способами: с периодом 0 и с периодом 9.

Давайте договоримся в дальнейшем не использовать бесконечные десятичные дроби с периодом 9. Вместо таких дробей будем записывать конечные десятичные дроби или бесконечные десятичные дроби с периодом 0.

Таким образом, можем сделать следующий вывод: каждое рациональное число можно представить в виде бесконечной периодической десятичной дроби. Справедливо и обратное утверждение: каждая бесконечная периодическая десятичная дробь является рациональным числом, так как может быть представлена в виде дроби , где m – целое число, n – натуральное число.

Вообще, при делении целого числа m на натуральное число n на некотором шаге остаток может стать равным нулю, тогда в результате деления получается целое число или конечная десятичная дробь. Либо же при делении целого числа m на натуральное число n на некотором шаге остатки начинают повторяться, так как каждый из остатков меньше n, тогда в результате деления получается бесконечная десятичная периодическая дробь.

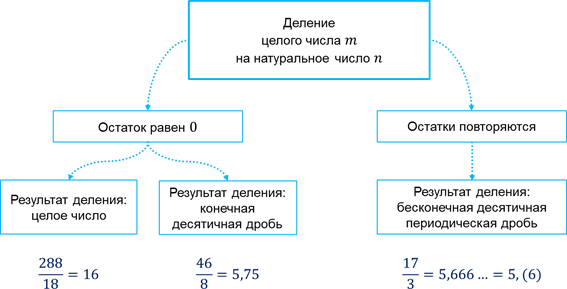
А теперь давайте приступим к практической части нашего урока.

Итак, задание первое. Запишите в виде бесконечной десятичной дроби: а) ;     б) .

Решение.

Задание второе. Запишите в виде обыкновенной дроби: а) ;     б) .

Решение.

И последнее задание. Покажите, что … .

Решение.