Площадь круга

Круг знаком вам так же хорошо, как и окружность. Круг – это часть плоскости, находящаяся внутри окружности, вместе с этой окружностью. Окружность – это граница круга. Иными словами, кругом называется часть плоскости, ограниченная окружностью. Круг радиуса R с центром О содержит точку О и все точки плоскости, находящиеся от точки О на расстоянии, не большем R.

Итак, выведем формулу для вычисления площади круга радиуса R. Пусть дан круг радиуса R и A₁A₂…A_n – правильный n-угольник, вписанный в окружность, которая ограничивает этот круг.

Не трудно заметить, что площадь многоугольника A₁A₂…A_n, так как этот многоугольник целиком содержится в данном круге. Понятно, что площадь  круга, вписанного в многоугольник, меньше площади  многоугольника, ведь этот круг целиком содержится в многоугольнике. Тогда имеем следующее двойное неравенство: , описанного около многоугольника.

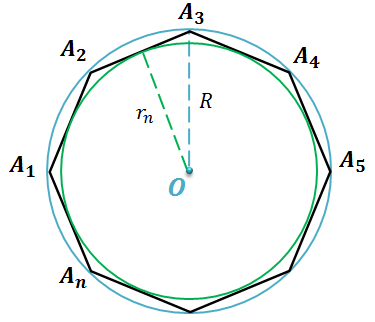
При неограниченном увеличении числа n сторон n-угольника радиус R_n вписанной окружности стремится к радиусу R описанной окружности
. Действительно, так как , то при неограниченном увеличении числа сторон n число , а значит,
, т.е. .

Иными словами, при неограниченном увеличении числа сторон многоугольника вписанная в него окружность «стремится» к описанной окружности, поэтому площадь
, при , при

Замечание. В течение веков усилия многих математиков были направлены на решение задачи, получившей название задача о квадратуре круга: построить при помощи циркуля и линейки квадрат, площадь которого равна площади данного круга. Только в конце 19 века было доказано, что такое построение невозможно.

Задача. Площадь круга  см². Найдите его диаметр.

Решение.

Мы уже знаем, что площадь круга вычисляется по формуле
.

 (см)

 (см)

Ответ:  см.

Задача. Найдите площадь круга, если площадь вписанного в этот круг квадрата равна  см² .

Решение.

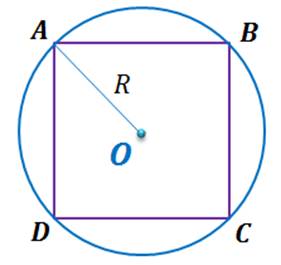
 (см).

 (см).

 (см²).

Ответ: .

Задача. Даны две концентрические окружности. Хорда большей окружности, равная  см, касается меньшей окружности. Найдите площадь кольца.

Решение.

Рассмотрим .

  – равнобедренный.

 – биссектриса, высота и медиана.

 (см).

Рассмотрим .

 (см²)

Ответ: .

Подведем итоги урока. На этом уроке мы рассмотрели такое понятие, как площадь круга. Вывели формулу для вычисления площади круга. А также решили задачи на применение этой формулы.