Кругом называется часть плоскости, ограниченная окружностью.
Круг радиуса  с центром
с центром  содержит
точку
содержит
точку  и все точки
плоскости, находящиеся от точки
и все точки
плоскости, находящиеся от точки  на
расстоянии, не большем
на
расстоянии, не большем  .
.
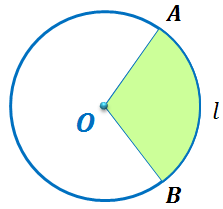
Если в круге провести два его радиуса, например, ОА и ОB, они выделят из круга его часть, которая называется сектором.
Определение. Круговым сектором или просто сектором называется часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.
Дуга, которая ограничивает сектор, называется дугой сектора.

На первом рисунке изображены два сектора с дугами АlB и АmB. Первый из этих секторов закрашен. На втором рисунке изображены круг, который касается всех сторон треугольника, и два сектора, ограниченные радиусами, проведенными в точки касания, и соответствующими дугами окружности.
Выведем формулу для
вычисления площади  радиусом
радиусом  , дуга которого имеет градусную меру
, дуга которого имеет градусную меру  .
.

Площадь круга радиусом  . Следовательно,
. Следовательно,  , ограниченного дугой в
, ограниченного дугой в  , равна
, равна  . Значит, Значит,
. Значит, Значит,  , ограниченного дугой в
, ограниченного дугой в  , выражается формулой:
, выражается формулой:  .
.
Например, если ABC –
равносторонний треугольник, вписанный в круг радиуса R, а точка О –
его центр, тогда площадь сектора, ограниченного радиусами ОА, ОB и
дугой AmB, равна  .
.

Теперь рассмотрим формулу для нахождения площади фигуры, которая называется сегментом.
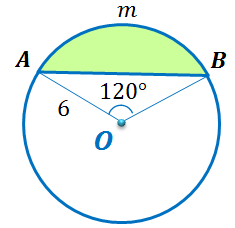
Определение. Круговым сегментом или просто сегментом называется часть круга, ограниченная дугой окружности и хордой, соединяющей концы этой дуги.

Дуга окружности, ограничивающая сегмент, называется дугой сегмента, а ограничивающая его хорда называется основанием сегмента.

На рисунке изображены два круговых сегмента, ограниченные хордой АB и дугами AlB и AmB. Хорда АB является основанием для каждого из этих сегментов. На втором рисунке изображены сегменты, ограниченные стороной MQ вписанного квадрата и соответствующими дугами окружности.
Вы уже знаете, что площадь
круга вычисляется по формуле  . Зная эту формулу нетрудно вывести формулу для
вычисления площади кругового сегмента. Рассмотрим два случая:
. Зная эту формулу нетрудно вывести формулу для
вычисления площади кругового сегмента. Рассмотрим два случая:
1) дуга сегмента меньше 180 градусов;
2) дуга сегмента больше 180 градусов.
Итак, первый случай.
Пусть дуга  сегмента имеет градусную меру
сегмента имеет градусную меру  , меньшую
, меньшую  .
.  .
.
Второй случай.
Пусть дуга  сегмента имеет градусную меру
сегмента имеет градусную меру  , большую
, большую  .
.
 .
.

Заметим, что площадь сегмента, градусная мера дуги которого α>180º, можно найти также как разность между площадью круга и площадью сегмента с тем же основанием и дугой, градусная мера которой равна 360º-α.

Если центральный угол
равен  , то этот сегмент – полукруг, и его площадь равна
, то этот сегмент – полукруг, и его площадь равна  .
.
Пусть ABC – равносторонний треугольник, вписанный в круг радиуса R, а точка О – его центр.

Тогда площадь меньшего сегмента, основанием которого служит сторона AB треугольника, равна
 .
.
Задача. Площадь сектора  см2, центральный угол равен
см2, центральный угол равен  . Найдите радиус круга.
. Найдите радиус круга.
Решение.




 (см)
(см)
 (см)
(см)
Ответ:  см.
см.
Задача. Чему равен  , если площадь сегмента
, если площадь сегмента  равна
равна  , радиус равен
, радиус равен  и центральный угол
и центральный угол  ?
?
Решение.


 (см)
(см)


Ответ:  .
.
Подведем итоги урока. На этом уроке мы познакомились с такими понятиями, как круговой сектор и круговой сегмент. Узнали, что круговым сектором или просто сектором называется часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга. Узнали, что круговым сегментом или просто сегментом называется часть круга, ограниченная дугой окружности и хордой, соединяющей концы этой дуги. А также вывели формулы для вычисления площади кругового сектора и кругового сегмента.

 Получите свидетельство
Получите свидетельство Вход
Вход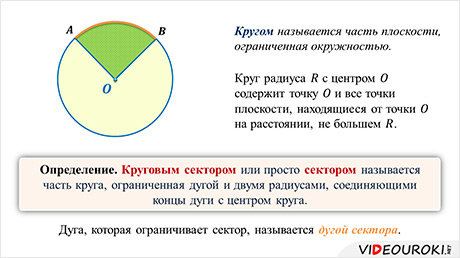



 0
0 11109
11109

