– Саш, привет. Чем занимаешься? Может, сходим погулять на улицу?
– Привет, Паша. Давай сходим, только сначала помоги мне разобраться с одной задачкой.
– Ну, давай.
– Мама купила коробку конфет весом 422 грамма. Мы всей семьёй её съели за ужином. Каждому досталось по 5 конфет. Но у меня вдруг возник вопрос: а сколько грамм конфет досталось каждому из нас?
Смотри, нас четверо: я, мама, сестра и папа. Вес конфет – 422 грамма. Вот я пробую поделить 422 на 4, а у меня нацело никак не получается поделить. Но мы все конфеты поделили нацело, значит и вес тоже должен поделиться без остатка.

– Да, интересно как-то получается. Я думаю, что, если мы пойдём в гости к Электроше, он нам сможет все объяснить.
– Электроша, здравствуй.
– Здравствуйте, мальчики.
– У нас новая задача. Мы не можем разделить 422 на 4, хотя точно знаем, что должно поделиться. Можешь нам объяснить, как такое делится?
– Конечно, сейчас я вам все объясню, но сначала давайте решим устно несколько заданий.

Прежде чем решить вашу задачу, давайте поговорим о делении десятичных дробей.
Сначала давайте вспомним, как понять запись  ? Паша, ты помнишь?
? Паша, ты помнишь?
– Это значит найти такое число с,
которое при умножение на  даёт число а.
даёт число а.

Это же правило выполняется и тогда, когда одно из чисел является десятичной дробью.
Например, разделим 1,6 на 2. Получим 0,8. Потому что если мы 0,8 умножим на 2, то получим 1,6.
Или если, например, мы разделим 1 на 2, то получим 0,5. Потому что при умножении 0,5 на 2 мы получим 1.
Но не всегда получается найти частное устно.
Например, давайте попробуем разделить 39,68 на 16.

– Ой, Электроша, а разве мы можем выполнить такое деление? Устно у нас точно не получится.
– Конечно, мальчики, мы можем разделить эти числа.
Умножим делимое на 100, и вместо десятичной дроби перед нами натуральное число 3968.
Тогда частное натуральных чисел будет в 100 раз больше искомого частного.
Разделим эти числа уголком и получим число 248. Теперь разделим это число на 100 и получим, что искомое частное равно 2,48.
Проверим правильность нашего деления. Умножим 2,48 на 16. Получим 39,68.

Теперь давайте попробуем эти же числа разделить по-другому. Начнём делить числа уголком, не обращая внимания на запятую. Сейчас мы сносим первую цифру после запятой. Поэтому и в частном поставим запятую. Продолжим деление до конца и получим 2,48.

– Вам понятно, ребята?
– Да, Электроша.
– Найдите частное чисел  .
.
Попробуй ты, Паша.
– Будем делить уголком. 4 на 8 не делится, разделим 42 на 8 – получим 5. Остаток равен 2. Сносим 5. Мы снесли первую цифру после запятой, значит, в частном после 5 ставим запятую. Продолжаем деление, и получим, что частное наших чисел равно 5,32.

– Молодец.
Теперь давайте попробуем найти частное вот
этих чисел  .
.
– Подожди, Электроша. Но здесь делимое меньше, чем делитель, разве такие числа можно делить?
– Да, Саша, и такие числа можно делить.
Запомните правило. Если делимое меньше делителя, то целая часть частного равна нулю.

Вернёмся к нашему частному. 1 на 5 не делится, значит, в частное запишем 0. Сносим 3 – значит, в частном после нуля ставим запятую. Делим дальше.
– Подожди, Электроша, но у нас осталась 2, а сносить уже больше нечего. Получается, что десятичные дроби на натуральные числа делятся с остатком?
– Нет, Саша, не совсем так.
Вы же помните, что если в десятичной дроби справа мы допишем нули, то число не изменится. Допишем 0. Снесём его и получим, что частное наших чисел равно 0,264.

Вам все понятно?
– Да, Электроша.
Тогда, Саша, попробуй найти частное вот этих чисел  .
.
2 < 4, значит, у нас будет 0 целых. Продолжаем делить. В остатке получим 2. Допишем 0, разделим и получим, что частное наших чисел равно 0,65.
Молодец.

Теперь давайте вернёмся к вашей задаче и попробуем разделить 422 на 4.
Разделим эти числа уголком, получим 105 целых. Цифры в делимом закончились, но мы можем поставить запятую и дописать после неё столько нулей, сколько нам нужно. Будем дописывать по одному нулю. Тогда получим, что каждый из вас съел по 105,5 граммов конфет.

– Ну как, мальчики, вам стало понятно?
– Да, Электроша.
– Тогда, Саша, попробуй найти частное чисел  .
.
Разделим уголком, получим 8 целых и 1 в остатке, допишем 0 и получим 8,2.
– Молодец, Саша.

Когда мы с вами знакомились с умножением десятичных дробей, то говорили, что если запятую перенести вправо на 1, 2 или 3 цифры, то число увеличится в 10, 100, 1000 и так далее раз, а если запятую перенести влево на 1, 2 или 3 цифры, то число уменьшится, соответственно, в 10, 100, 1000 и так далее раз.

Из этого правила можно вывести правило деления десятичных дробей на 10, 100, 1000 и так далее.
Чтобы разделить десятичную дробь на десять, сто, тысячу и так далее, надо в записи этой дроби перенести запятую влево на одну, две, три и так далее цифры.

Выполним задание.
Найти частное чисел:  .
.
– Саша, начинай ты.
В первом примере нам нужно перенести запятую на 1 цифру влево, получим 5,263.
Во втором примере запятую перенесём на 2 цифры влево и получим 1,258.
Молодец.

Ещё раз давайте посмотрим на все примеры, которые мы сегодня решали.

Что у них общего? Паша, ты как думаешь?
– Так, надо подумать. Я понял. Во всех этих примерах делителями были натуральные числа. А вот интересно, может ли делителем быть десятичная дробь?
– Да, Паша, может.
Давайте попробуем перевести в граммы
следующее количество килограмм:  кг,
кг,  кг,
кг,  кг.
кг.

Посмотрите, у нас получилось, что 600 грамм
можно записать несколькими способами. Заменяя дроби делением, получим, что  . Другими словами, можно записать правило. Если делимое и делитель
увеличить одновременно в десять, сто, тысячу и так далее раз, то частное не
изменится.
. Другими словами, можно записать правило. Если делимое и делитель
увеличить одновременно в десять, сто, тысячу и так далее раз, то частное не
изменится.

Используя это правило, давайте попробуем найти частное чисел.
Увеличим делимое и делитель одновременно в 10 раз. Получим деление на натуральное число. Чему оно равно, нам найти несложно. Остаётся только полученное число разделить на 10, и получим, что частное равно 24,8.

Сформулируем и запомним правило:
Чтобы разделить десятичную дробь на десятичную, надо:
Первое. Перенести в делимом и делителе запятые вправо на столько цифр, сколько их содержится после запятой в делителе.
И второе. Выполнить деление на натуральное число.

– Ну что, мальчики, вам стало понятно?
– Да.
– Тогда для вас задание.
Вычислите:  .
.
Паша, это задание для тебя.
В первом примере в делителе после запятой 2 знака, значит, перенесём запятые делимого и делителя на 2 цифры вправо. Теперь нам остаётся только поделить числа.
Получим 30,8.
Во втором примере перенесём запятые делимого и делителя на 2 цифры вправо. Выполним деление чисел и получим 240.

– Молодец, вот для вас ещё одно задание.
Решите уравнение  .
.
– Саша, это задание для тебя.
Найдём сначала коэффициент перед
 . Для этого вынесем
. Для этого вынесем  за скобки. Получим
за скобки. Получим  . Получим, что уравнение можно записать так
. Получим, что уравнение можно записать так Тогда
Тогда  . Для того чтобы разделить на десятичную
дробь, перенесём в делимом и делителе запятые на 2 знака вправо. Разделим
уголком и получим, что
. Для того чтобы разделить на десятичную
дробь, перенесём в делимом и делителе запятые на 2 знака вправо. Разделим
уголком и получим, что  .
.

– Молодец, Саша.

 Получите свидетельство
Получите свидетельство Вход
Вход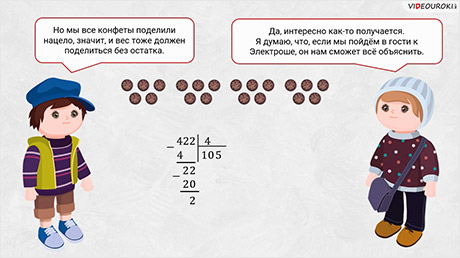



 4
4 8826
8826


Любовь, данный комплект есть, называется "Математика 5 класс ФГОС". Вам нужно зайти сразу в свой личный кабинет и именно через него выбрать раздел "Учебник". Появится список комплектов, и в этом списке есть данный комплект.
Захожу, но этого комлекта в > учебник< нет. Есть другие, а тот который мне нужен нет.
Здравствуйте, Любовь. Вам нужно зайти в свой личный кабиент с аккаунта, с которого был куплен заказ -> учебник -> выбрать данный комплект и нажать возле нужного задания "Раздать урок".
Здравствуйте. Я купила этот комплект. Мне нужен для изучения деления дес.дробей именно этот урок. В свободном доступе его нет. Как я могу детям дать дома его посмотреть?