Представим себе такую историю…
– Паша, над чем это ты задумался? – спросил у друга Саша.
– Знаешь, Саша, я захотел сравнить температуру воздуха на улице за последнюю неделю, – ответил Паша.
– И что же здесь сложного? – удивился Саша. – Мы же умеем сравнивать числа.
–
Ну вот, смотри, – начал Саша, – в понедельник температура была равна  . Во вторник была
. Во вторник была 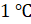 . В среду она
стала
. В среду она
стала 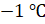 . В четверг
столбик термометра опустился до
. В четверг
столбик термометра опустился до 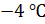 . В пятницу было
уже
. В пятницу было
уже 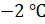 . В субботу было
. В субботу было 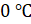 . А в воскресенье температура
была
. А в воскресенье температура
была 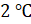 .
.

– А как сравниваются отрицательные числа? – спросил Саша.
– Вот и я не знаю, – ответил Паша. – Давай спросим у Мудряша.
– Ребята, прежде чем я отвечу на ваш вопрос, давайте немного разомнёмся и выполним устные задания, – предложил Мудряш.
– Теперь сверимся! – сказал Мудряш. – Посмотрите, что у вас должно было получиться!
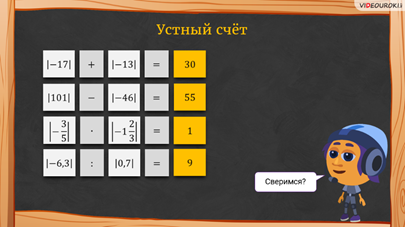
– А сейчас можем вернуться к вашему вопросу, – начал Мудряш. – Ребята, вы уже умеете сравнивать любые положительные числа друг с другом и 0. У вас возник вопрос, можно ли сравнивать отрицательные числа и как это делать? Конечно, можно! И сегодня на уроке мы научимся сравнивать отрицательные числа с положительными, отрицательные числа с 0 и отрицательные числа друг с другом.
Вам известно, что на координатном луче из двух чисел большее число расположено правее меньшего. То же самое мы можем сказать и про координатную прямую.
Давайте начертим координатную прямую. Отметим на ней начало отсчёта. Выберем единичный отрезок.
Отметим
на нашей координатной прямой значения температуры воздуха за последнюю неделю. В
понедельник было  тепла. Отметим это
точкой А (3). Во вторник был
тепла. Отметим это
точкой А (3). Во вторник был 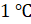 . Отметим это
точкой В (1). В среду термометр
показывал
. Отметим это
точкой В (1). В среду термометр
показывал 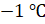 . Это отметим
точкой С (
. Это отметим
точкой С (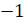 ). В четверг
столбик термометра опустился до
). В четверг
столбик термометра опустился до 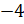 . Это значение мы
отметим точкой D (
. Это значение мы
отметим точкой D (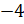 ).
В пятницу было
).
В пятницу было 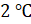 мороза, а значит,
на координатной прямой отметим точку Е (
мороза, а значит,
на координатной прямой отметим точку Е (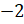 ).
).
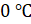 в субботу отметим
точкой О. В воскресенье уже было
в субботу отметим
точкой О. В воскресенье уже было 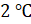 . Отметим это
точкой P (2).
. Отметим это
точкой P (2).

–
В понедельник была самая тёплая погода, поэтому точка А (3)
расположена правее всех остальных точек, – сказали Паша и Саша. – А в четверг был
самый холодный день, поэтому точка D
(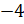 ) расположена
левее других точек.
) расположена
левее других точек.
–
Всё верно! Молодцы! – похвалил мальчишек Мудряш и продолжил, – мы можем
записать, что 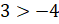 . При этом обратите
внимание, что все положительные числа расположены правее отрицательных чисел. А
значит, любое положительное число больше любого отрицательного числа.
. При этом обратите
внимание, что все положительные числа расположены правее отрицательных чисел. А
значит, любое положительное число больше любого отрицательного числа.
Давайте
рассмотрим точку D (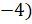 и
точку С (
и
точку С (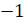 ). Точка D
лежит левее точки C,
то есть
). Точка D
лежит левее точки C,
то есть  . При этом
заметим, что модуль
. При этом
заметим, что модуль 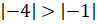 .
.
– То есть получается, что из двух отрицательных чисел меньше то, чей модуль больше? – заметили Паша и Саша.
– Совершенно верно! – отметил Мудряш и сказал, – запомните! На координатной прямой из двух чисел большее число расположено правее меньшего. Любое положительное число больше любого отрицательного числа. Из двух отрицательных чисел меньше то, модуль которого больше.

Вернёмся к координатной прямой. Посмотрите, число 0 расположено левее любого положительного числа и правее любого отрицательного числа, – сказал Мудряш.
– А значит, любое положительное число больше 0, а любое отрицательное число меньше 0, – сделали вывод мальчики.
–
Молодцы! – похвалил Мудряш ребят и продолжил, – если a
– положительное число, то записывают неравенство: 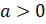 .
.
–
Если a – отрицательное число,
то записывают:  , – подсказали
мальчики.
, – подсказали
мальчики.
–
Верно! Если же a – неотрицательное
число, то пишут: 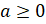 , – продолжил
Мудряш.
, – продолжил
Мудряш.
–
Если же a – неположительное число,
то пишут: 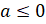 , – снова
подсказали ребята.
, – снова
подсказали ребята.
– Молодцы! – похвалил Сашу и Пашу Мудряш и продолжил, – а теперь с помощью рассмотренных обозначений запишем свойство модуля. Что вы знаете о модуле?
–
Мы знаем, что 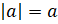 , если a
– неотрицательное число, – начал Паша.
, если a
– неотрицательное число, – начал Паша.
–
И что 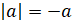 , если a
–
отрицательное число, – добавил Саша.
, если a
–
отрицательное число, – добавил Саша.
– Всё верно! – сказал Мудряш. – Теперь мы с вами можем записать это следующим образом:
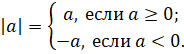
Запомните! Любое
отрицательное число меньше нуля, любое положительное число больше нуля. Если a
– положительное число, то пишут: 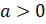 . Если a
– отрицательное число, то пишут:
. Если a
– отрицательное число, то пишут:  . Если a
–
неотрицательное число, то пишут:
. Если a
–
неотрицательное число, то пишут: 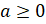 . Если a
– неположительное число, то пишут:
. Если a
– неположительное число, то пишут: 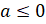 .
.
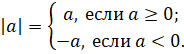

А теперь выполним несколько заданий.
Задание первое: сравните числа:
а)
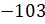 и
и 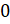 ;
б)
;
б) 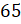 и
и 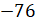 ;
в)
;
в) 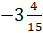 и
и 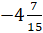 ; г)
; г) 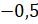 и
и 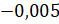 .
.
Решение: 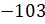 и
и 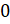 .
Мы знаем, любое отрицательное число меньше 0.
Значит,
.
Мы знаем, любое отрицательное число меньше 0.
Значит,  .
.
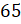 и
и 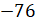 .
Любое положительное число больше любого отрицательного числа, а значит,
.
Любое положительное число больше любого отрицательного числа, а значит, 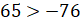 .
.
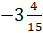 и
и 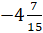 . Оба числа
отрицательные. Из двух отрицательных чисел меньше то, модуль которого больше.
. Оба числа
отрицательные. Из двух отрицательных чисел меньше то, модуль которого больше.  ;
; 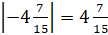 . Мы знаем, что из
двух смешанных чисел больше то, целая часть которого больше. То есть
. Мы знаем, что из
двух смешанных чисел больше то, целая часть которого больше. То есть 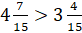 . Тогда
. Тогда 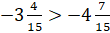 .
.
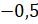 и
и 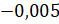 .
Снова сравниваем два отрицательных числа. Найдём их модули.
.
Снова сравниваем два отрицательных числа. Найдём их модули.  ;
; 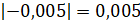 . Модуль
первого числа больше, чем модуль второго. Значит,
. Модуль
первого числа больше, чем модуль второго. Значит, 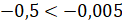 .
.

Второе
задание: расположите числа 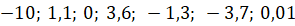 в порядке
убывания.
в порядке
убывания.
Решение: Из всех чисел выберем наибольшее. Мы с вами знаем, что любое положительное число больше любого отрицательного числа. Из всех положительных чисел наибольшим является 3,6. Запишем его. Следующее наибольшее положительное число из оставшихся у нас 1,1. Запишем его. И последнее положительное число – это 0,01. Запишем его.
У
нас остались отрицательные числа и 0.
Любое отрицательное число меньше 0.
А значит, следующим в наш ряд запишем число 0.
Чтобы сравнить отрицательные числа, давайте найдём их модули: 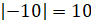 ;
; 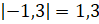 ;
; 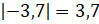 . Мы с вами знаем,
что из двух отрицательных чисел меньше то, модуль которого больше. Наименьшее
значение модуля имеет число
. Мы с вами знаем,
что из двух отрицательных чисел меньше то, модуль которого больше. Наименьшее
значение модуля имеет число 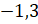 . Значит, оно
наибольшее из всех отрицательных чисел. Запишем его. Следующее наименьшее
значение модуля имеет число
. Значит, оно
наибольшее из всех отрицательных чисел. Запишем его. Следующее наименьшее
значение модуля имеет число 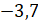 . Значит,
следующим в наш ряд запишем число
. Значит,
следующим в наш ряд запишем число 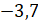 . И последним
запишем число
. И последним
запишем число 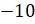 . Оно является
самым наименьшим.
. Оно является
самым наименьшим.
Вот таким образом мы расположили данные числа в порядке убывания.

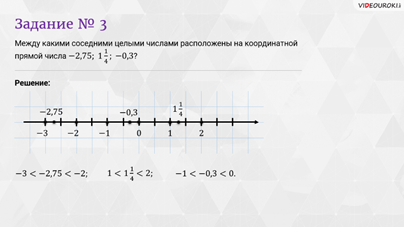
Следующее
задание: между какими соседними целыми числами расположены на
координатной прямой данные числа 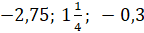 ?
?
Решение: для большей наглядности начертим координатную прямую. Отметим на ней начало отсчёта. За единичный отрезок возьмём 2 клеточки.

Итак,
первое число у нас 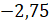 . Отметим его на
координатной прямой. Затем отметим ближайшие к нему целые числа. Это числа
. Отметим его на
координатной прямой. Затем отметим ближайшие к нему целые числа. Это числа 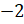 и
и
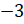 . Записать ответ
на вопрос задачи мы с вами можем в виде двойного неравенства:
. Записать ответ
на вопрос задачи мы с вами можем в виде двойного неравенства: 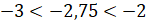 .
.

Следующее
число у нас 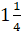 . Отметим его на
нашей координатной прямой, а также ближайшие к нему целые числа 1
и 2.
Тогда записать ответ на вопрос задачи можно в виде двойного неравенства:
. Отметим его на
нашей координатной прямой, а также ближайшие к нему целые числа 1
и 2.
Тогда записать ответ на вопрос задачи можно в виде двойного неравенства: 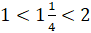 .
.

И
ещё одно число – это 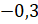 . Отметим его на
координатной прямой. Рядом с ним находятся целые числа – 0
и
. Отметим его на
координатной прямой. Рядом с ним находятся целые числа – 0
и 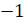 . Тогда записать
ответ на вопрос задачи можно в виде двойного неравенства:
. Тогда записать
ответ на вопрос задачи можно в виде двойного неравенства: 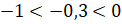 .
.

И
последнее задание: известно, что x
и y – положительные числа, a
и b –
отрицательные числа. Сравните: а) 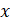 и
и 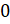 ;
б)
;
б)  и
и 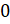 ;
в)
;
в) 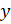 и
и 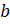 ;
г)
;
г)  и
и 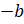 ; д)
; д) 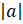 и
и  .
.
Решение: 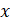 и
и
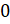 . Так как по
условию x – положительное число, а
любое положительное число больше 0,
то получаем неравенство:
. Так как по
условию x – положительное число, а
любое положительное число больше 0,
то получаем неравенство: 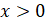 .
.
Сравним
 и
и 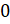 .
У нас a – отрицательное число, а
значит, противоположное ему число
.
У нас a – отрицательное число, а
значит, противоположное ему число  будет
положительным, то есть
будет
положительным, то есть 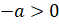 .
.
Сравним
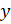 и
и 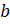 .
У нас y положительное
число, а b – отрицательное. Мы с
вами знаем, что любое положительное число больше любого отрицательного числа. Значит,
.
У нас y положительное
число, а b – отрицательное. Мы с
вами знаем, что любое положительное число больше любого отрицательного числа. Значит,
 .
.
Сравним
 и
и 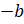 . Число a
у нас отрицательное число. Число
. Число a
у нас отрицательное число. Число 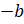 противоположно
отрицательному числу b,
а значит, является положительным, то есть
противоположно
отрицательному числу b,
а значит, является положительным, то есть  . Любое
положительное число больше любого отрицательного числа. Тогда мы с вами запишем
неравенство:
. Любое
положительное число больше любого отрицательного числа. Тогда мы с вами запишем
неравенство: 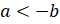 .
.
И
последнее: 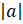 и
и  .
Число a у нас отрицательное. Его
модуль будет положительным. Так как любое положительное число больше любого
отрицательного числа, то будет верным неравенство:
.
Число a у нас отрицательное. Его
модуль будет положительным. Так как любое положительное число больше любого
отрицательного числа, то будет верным неравенство: 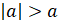 .
.


 Получите свидетельство
Получите свидетельство Вход
Вход



 0
0 2714
2714