Представим себе такую историю…
– Привет, Паша! Чем ты занимаешься? – спросил у друга Саша.
– Я собираюсь разгадать ребус, – ответил Паша. – Давай разгадаем его вместе.
– Давай, – сказал Саша.

– Смотри, – показал ребус другу Паша. – Здесь нарисован перевёрнутый дом и пульт с запятыми.
– А почему дом перевёрнут? – спросил Саша.
– Это означает, что слово «дом» надо читать справа налево, – пояснил Паша. – То есть получаем слово «мод».
– Вторая картинка в ребусе – пульт. Что означают запятые перед и после картинки? – задал вопрос Саша.
– Запятые в ребусе означают, что из названия картинки нам нужно исключить столько букв, сколько стоит запятых, – объяснил Паша.
– Значит, в слове «пульт» мы уберём первую и последнюю буквы, – неуверенно сказал Саша.
– Верно! – отметил Паша. – Мы уберём буквы «п» и «т».
– И у нас останется слово «уль», – подсказал другу Саша.
– А теперь из получившихся слов «мод» и «уль» составим слово «модуль», – сказал Паша.

– А что оно означает? – спросил Саша.
– Не знаю. Давай спросим у Мудряша, – ответил Паша.
– Ребята, прежде чем я отвечу на ваш вопрос, давайте немного разомнёмся и выполним устные задания, – предложил Мудряш.
– Теперь сверимся! – сказал Мудряш. – Посмотрите, что у вас должно было получиться!

–
А сейчас можем вернуться к вашему вопросу, – начал Мудряш. – Ребята, давайте на
координатной прямой отметим точку А (4)
и точку В (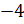 ). Эти точки имеют разные
координаты, но и точка А, и точка В расположены на расстоянии 4
единичных отрезков от начала отсчёта.
). Эти точки имеют разные
координаты, но и точка А, и точка В расположены на расстоянии 4
единичных отрезков от начала отсчёта.
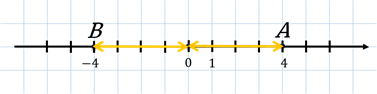
Для
такого расстояния и придумано название модуль числа. Тогда можно
сказать, что числа 4 и 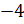 имеют
одинаковые модули, равные 4. Записывают это вот
таким образом:
имеют
одинаковые модули, равные 4. Записывают это вот
таким образом: 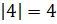 и
и 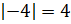 .
.
Обратите внимание! Так как расстояние не может быть отрицательным, то и модуль числа не может быть отрицательным.
– Запомните! – сказал Мудряш. – Модулем числа а называют расстояние от начала отсчёта до точки, изображающей это число на координатной прямой.
Модуль
числа a обозначают
так: 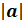 . И читают: «модуль числа
а».
. И читают: «модуль числа
а».
Модуль числа принимает только неотрицательные значения.

–
Давайте найдём модули чисел 3; 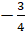 ;
; 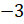 ;
0
и 2,5,
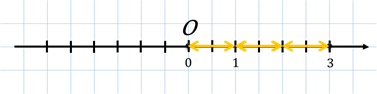
– предложил Мудряш. – Начертим координатную прямую. Отметим на ней начало
отсчёта точкой О. А за единичный отрезок возьмём 2 клеточки. Первое
число у нас 3. Отметим его на координатной прямой.
Расстояние от начала координат до него равно 3 единичным отрезкам, а значит,
;
0
и 2,5,
– предложил Мудряш. – Начертим координатную прямую. Отметим на ней начало
отсчёта точкой О. А за единичный отрезок возьмём 2 клеточки. Первое
число у нас 3. Отметим его на координатной прямой.
Расстояние от начала координат до него равно 3 единичным отрезкам, а значит, 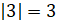 .
.
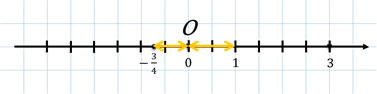
Второе
число у нас 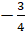 . Отметим его на
координатной прямой. Расстояние от начала координат до него равно
. Отметим его на
координатной прямой. Расстояние от начала координат до него равно  единичного
отрезка. А значит,
единичного
отрезка. А значит, 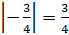 .
.
Затем
число 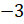 . Отметим его. Расстояние
до него от начала координат равно 3 единичным
отрезкам, то есть
. Отметим его. Расстояние
до него от начала координат равно 3 единичным
отрезкам, то есть 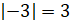 .
.
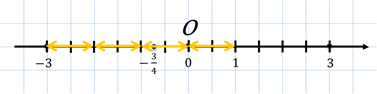
Следующее
число у нас 0. 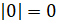 , так как точка с
координатой 0 совпадает с началом отсчёта.
, так как точка с
координатой 0 совпадает с началом отсчёта.
И
ещё одно число – 2,5. Отметим его на нашей
координатной прямой. Расстояние от начала отсчёта до него равно 2,5
единичным отрезкам, а значит, 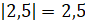 .
.
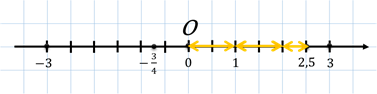
Обратите
внимание, что модулями положительных чисел 3
и 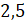 , а также 0
являются сами эти числа. А вот модулями отрицательных чисел
, а также 0
являются сами эти числа. А вот модулями отрицательных чисел 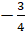 и
и 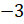 являются
противоположные им числа
являются
противоположные им числа  и 3.
Причём модули противоположных чисел 3
и
и 3.
Причём модули противоположных чисел 3
и 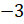 равны.
равны.
–
Запомните! – сказал Мудряш. – Модуль неотрицательного числа равен этому
числу. То есть 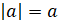 , если a
– неотрицательное число. Модуль отрицательного числа равен противоположному числу.
То есть
, если a
– неотрицательное число. Модуль отрицательного числа равен противоположному числу.
То есть 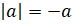 , если a
– отрицательное число. Модули противоположных чисел равны. То есть
, если a
– отрицательное число. Модули противоположных чисел равны. То есть 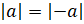 .
.

А теперь выполним несколько заданий.
Задание первое: найдите значения выражений:
а)
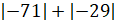 ; б)
; б) 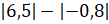 ; в)
; в) 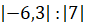 ; г)
; г) 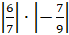 .
.
Решение: в
выражении 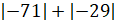 надо найти сумму модуля
числа
надо найти сумму модуля
числа 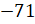 и модуля числа
и модуля числа 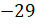 .
Найдём:
.
Найдём: 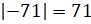 ;
; 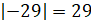 . Сумма чисел 71
и 29
равна 100.
. Сумма чисел 71
и 29
равна 100.
В
выражении 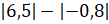 надо вычислить разность
модулей чисел 6,5 и
надо вычислить разность
модулей чисел 6,5 и 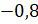 .
Найдём:
.
Найдём: 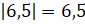 ;
; 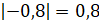 . Разность чисел 6,5
и 0,8
равна 5,7.
. Разность чисел 6,5
и 0,8
равна 5,7.
В
выражении 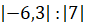 надо
найти частное модуля
надо
найти частное модуля 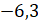 и модуля 7.
Найдём:
и модуля 7.
Найдём: 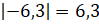 ;
; 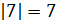 . Частное чисел 6,3
и 7
равно 0,9.
. Частное чисел 6,3
и 7
равно 0,9.
И
в последнем выражении 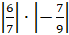 надо найти произведение
модулей дробей
надо найти произведение
модулей дробей  и
и 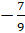 . Найдём:
. Найдём: 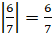 ;
; 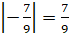 . Запишем произведение
этих дробей:
. Запишем произведение
этих дробей: 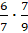 . Выполним сокращение
числителя и знаменателя на 3 и на 7.
И получим
. Выполним сокращение
числителя и знаменателя на 3 и на 7.
И получим  .
.

Второе задание: найдите:
а) положительное число, модуль которого равен 9; 7,1;
б)
отрицательное число, модуль которого равен  ; 85.
; 85.
Решение: мы
знаем, что 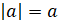 . Воспользовавшись этим
равенством справа налево, мы можем записать, что
. Воспользовавшись этим
равенством справа налево, мы можем записать, что 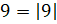 , а
, а 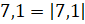 .
.
Модуль
отрицательного числа равен противоположному числу, то есть 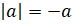 .
Воспользовавшись этим равенством справа налево, можем записать, что одна
.
Воспользовавшись этим равенством справа налево, можем записать, что одна 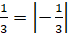 , а
, а 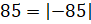 .
.

Следующее
задание: расположите числа 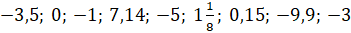 в порядке возрастания их
модулей.
в порядке возрастания их
модулей.
Решение:
сначала нам надо найти модули данных чисел. Итак, 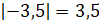 ;
; 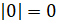 ;
; 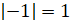 ;
; 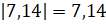 ;
; 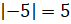 ;
; 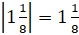 ;
; 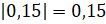 ;
; 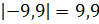 и
и 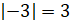 .
.
Нам
надо расположить числа в порядке возрастания их модулей. Наименьший модуль
имеет число 0. Запишем его первым. Следующее наименьшее
значение модуля имеет число 0,15. Записываем его. Далее наименьший
модуль у числа 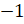 . Следующее наименьшее
значение имеет модуль
. Следующее наименьшее
значение имеет модуль 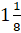 . Записываем
. Записываем 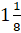 . Затем записываем число
. Затем записываем число 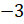 ,
так как его модуль самый меньший из оставшихся. За ним будет идти
,
так как его модуль самый меньший из оставшихся. За ним будет идти 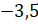 .
Следующее наименьшее значение модуля имеет число
.
Следующее наименьшее значение модуля имеет число 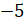 .
Записываем его. Далее будет идти 7,14.
Самое большое значение модуля имеет число
.
Записываем его. Далее будет идти 7,14.
Самое большое значение модуля имеет число 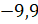 .
Записываем его последним.
.
Записываем его последним.

И последнее задание: решите уравнения:
а)
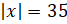 ; б)
; б) 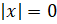 ; в)
; в) 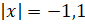 .
.
Решение: для
решения этих уравнений мы воспользуемся известными равенствами: 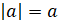 , если a
– неотрицательное число;
, если a
– неотрицательное число; 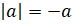 , если a
– отрицательное число.
, если a
– отрицательное число.
Первое
уравнение. Если модуль 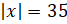 , то
, то 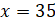 или
или 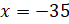 , так как
, так как 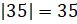 и
и 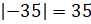 .
.
Второе
уравнение: 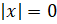 . Решением этого
уравнения является
. Решением этого
уравнения является 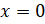 , так как только
, так как только 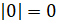 .
.
И
последнее уравнение 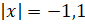 не имеет решений, так
как модуль не может быть отрицательным.
не имеет решений, так
как модуль не может быть отрицательным.


 Получите свидетельство
Получите свидетельство Вход
Вход



 0
0 6316
6316

