Представим себе такую историю…
– Привет, Паша! – поздоровался с другом Саша. – Извини, что опоздал.
– Что случилось? – поинтересовался Паша.
– Ничего не случилось. Просто когда мы договаривались встретиться в кафе, ты сказал, что мне нужно выйти из автобуса и пройти дальше по тротуару 100 метров. Но ты не сказал, в какую сторону надо идти, – говорил немного расстроенный Саша.
– После того, как ты вышел из автобуса, надо было идти дальше по направлению движения автобуса, то есть повернуть налево и пройти 100 метров, – пояснил Паша.

– А я повернул направо и прошёл 100 метров, – сказал Саша.
– Извини, что так вышло. Ты прошёл 100 метров, но в противоположном направлении. А давай мы об этом поговорим с Мудряшом, – предложил другу Паша.
– Давай, – согласился с ним Саша.
– Ребята, прежде чем мы с вами поговорим, давайте немного разомнёмся и выполним устные задания, – предложил Мудряш.
– Теперь сверимся! – сказал Мудряш. – Посмотрите, что у вас должно было получиться!
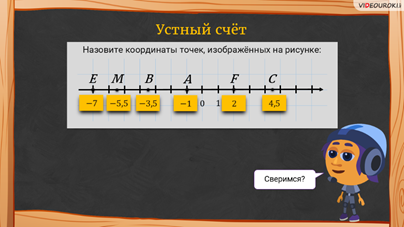
– А сейчас можем вернуться к вашему вопросу, – начал Мудряш. – На прошлом уроке мы с вами ввели понятие координатной прямой. Напомним, что координатной прямой называют прямую, на которой выбрали начало отсчёта, единичный отрезок и направление.
Начертим координатную прямую. Отметим на ней начало отсчёта. Пусть длина единичного отрезка равна 20 метрам. Представим, что автобусная остановка, на которой вышел Саша, расположена в начале отсчёта. Паша сказал Саше, что кафе находится в 100 метрах от автобусной остановки, но не уточнил, в какую сторону нужно идти Саше.
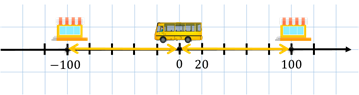
Если
бы кафе было расположено справа от автобусной остановки, то есть от начала
отсчёта, то на координатной прямой ему бы соответствовала точка 100.
А если бы слева, то ему бы соответствовала бы точка 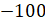 .
.
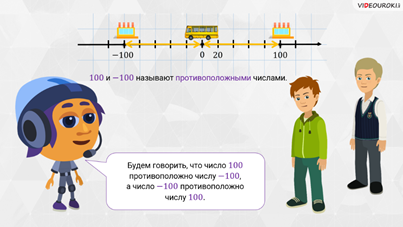
То
есть получается, чтобы попасть из начала в эти точки, надо пройти одинаковые
расстояния, но в противоположных направлениях. Тогда числа 100
и 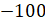 называют
противоположными. Будем говорить, что число 100
противоположно числу
называют
противоположными. Будем говорить, что число 100
противоположно числу 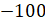 ,
а число
,
а число 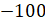 противоположно
числу 100.
противоположно
числу 100.
Давайте ещё приведём примеры противоположных чисел.
–
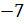 и 7;
30,9
и
и 7;
30,9
и 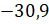 ;
;
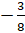 и
и
 ,
– начали перечислять мальчики, и у них возник вопрос, – а какое число является
противоположным числу 0?
,
– начали перечислять мальчики, и у них возник вопрос, – а какое число является
противоположным числу 0?
–
Запомните! – сказал Мудряш. – Число 0 противоположно
самому себе. Число, противоположное числу a,
обозначают как 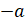 .
.

–
Обратите внимание, – продолжил Мудряш, – что, поставив, например, перед положительным
числом 15
знак
«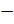 »,
мы получим число
»,
мы получим число 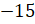 ,
противоположное 15. Приписав перед
отрицательным числом
,
противоположное 15. Приписав перед
отрицательным числом 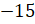 знак
«
знак
«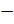 »,
мы получим число 15, противоположное
»,
мы получим число 15, противоположное 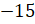 .
.

–
Запомните! – сказал Мудряш. – Число, противоположное числу 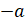 ,
равно числу а. То есть верно следующее равенство:
,
равно числу а. То есть верно следующее равенство: 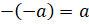 .
Обратите внимание, что использование скобок в этом равенстве обязательно.
.
Обратите внимание, что использование скобок в этом равенстве обязательно.

– Получается, что каждое число имеет противоположное ему число? – спросили ребята.
– Да, и только одно, – сказал Мудряш и добавил, – запомните! Все натуральные числа, противоположные им числа и 0 называют целыми числами. Натуральные числа называют целыми положительными числами. А числа, противоположные натуральным, называют целыми отрицательными числами.

–
Тогда как называют числа, например, 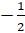 ;
3,5;
;
3,5;
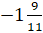 ?
– спросили мальчишки.
?
– спросили мальчишки.
– Такие числа называются дробными числами, – ответил Мудряш. – Запомните! Целые и дробные числа называют рациональными числами.

– Давайте приведём примеры рациональных чисел, – предложил Мудряш.
–
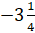 ;
2;
105;
;
2;
105;
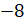 ; 0;
; 0;
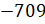 ;
;  ,
– привели примеры Саша и Паша.
,
– привели примеры Саша и Паша.
– Хорошо! А сейчас составим следующую схему, – сказал Мудряш. – Мы сказали, что рациональными называют целые и дробные числа. Целыми числами называют натуральные числа, 0 и числа, противоположные натуральным. Дробными числами являются положительные и отрицательные дроби.
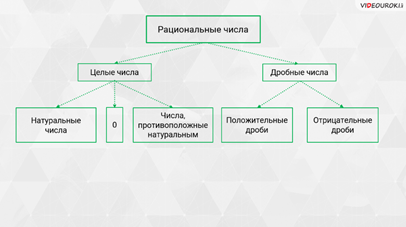
А теперь давайте выполним несколько заданий.
Задание
первое: найдите числа, противоположные числам 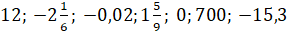 .
.
Решение: первое
число у нас 12. Припишем перед ним знак «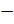 »
и получим противоположное ему число
»
и получим противоположное ему число 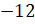 .
.
Второе
число у нас 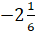 .
Припишем перед ним знак «
.
Припишем перед ним знак «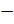 ».
Воспользовавшись равенством
».
Воспользовавшись равенством 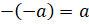 ,
получим противоположное ему число
,
получим противоположное ему число 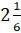 .
.
Следующее
число у нас 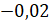 .
Поставим перед ним знак «
.
Поставим перед ним знак «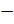 ».
Воспользовавшись равенством
».
Воспользовавшись равенством 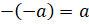 ,
получим противоположное число
,
получим противоположное число 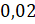 .
.
Перед
числом 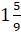 поставим
знак «
поставим
знак «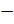 »
и получим противоположное число
»
и получим противоположное число 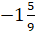 .
.
Противоположным числу 0 является само число 0.
Следующее
число у нас 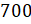 .
Припишем перед ним знак «
.
Припишем перед ним знак «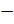 »
и получим противоположное число
»
и получим противоположное число 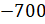 .
.
Перед
числом 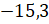 припишем
знак «
припишем
знак «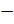 ».
Воспользовавшись равенством
».
Воспользовавшись равенством 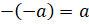 ,
получим противоположное число
,
получим противоположное число 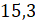 .
.

Следующее
задание: выберите из чисел 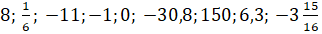 натуральные,
целые, отрицательные, неотрицательные, дробные.
натуральные,
целые, отрицательные, неотрицательные, дробные.
Решение: давайте заполним следующую таблицу.

Число 8 мы можем отнести к натуральным числам, целым и неотрицательным. Напомним, что к неотрицательным числам относятся положительные числа и 0.
 отнесём
к неотрицательным и дробным.
отнесём
к неотрицательным и дробным.
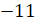 у
нас – целое отрицательное число.
у
нас – целое отрицательное число.
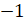 также
отнесём к целым и отрицательным.
также
отнесём к целым и отрицательным.
0 отнесём к целым и неотрицательным.
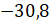 к
отрицательным числам и дробным.
к
отрицательным числам и дробным.
150 запишем к натуральным, целым и неотрицательным.
6,3 отнесём к неотрицательным числам и дробным.
И
последнее число у нас 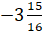 .
Его мы
запишем к отрицательным числам и дробным.
.
Его мы
запишем к отрицательным числам и дробным.

И
ещё одно задание: решите уравнения: а) 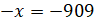 ;
б)
;
б) 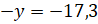 ;
в)
;
в) 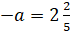 .
.
Решение:
первое уравнение: 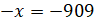 .
Чтобы его решить, воспользуемся уже известным нам равенством
.
Чтобы его решить, воспользуемся уже известным нам равенством 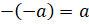 ,
но справа налево. Тогда можем записать, что
,
но справа налево. Тогда можем записать, что 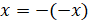 .
Подставим
.
Подставим 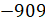 вместо
вместо
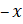 .
И
получим, что
.
И
получим, что 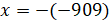 .
Следовательно,
.
Следовательно, 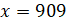 .
.
Второе
уравнение: 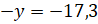 .
Также воспользуемся равенством
.
Также воспользуемся равенством 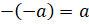 .
Тогда можем записать, что
.
Тогда можем записать, что 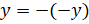 .
Подставим
.
Подставим 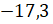 вместо
вместо
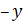 .
Получим, что
.
Получим, что 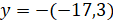 .
Откуда
.
Откуда
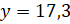 .
.
И
последнее уравнение: 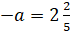 .
Снова воспользуемся равенством
.
Снова воспользуемся равенством 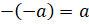 ,
но справа налево:
,
но справа налево: 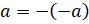 .
Подставим
.
Подставим
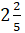 вместо
вместо
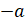 .
И получим, что
.
И получим, что 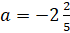 .
.


 Получите свидетельство
Получите свидетельство Вход
Вход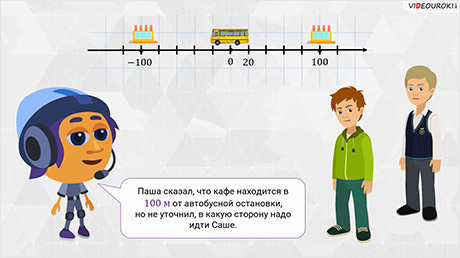



 0
0 3181
3181

