Представим себе такую историю…
– И как же мне узнать-то? – задумался Саша.
– Что случилось? – поинтересовался у друга Паша.
– Мы с родителями собрали 27 литров берёзового сока, – начал рассказывать Саша. – Мама сказала к вечеру подготовить трёхлитровые банки, чтобы закатать сок.
– Здорово! – обрадовался за друга Паша. – Берёзовый сок очень полезный! Так, а что ты там не мог узнать?
– Не могу понять, сколько мне нужно подготовить банок, – расстроенно ответил Саша.
– Ну, давай подумаем вместе! – предложил Паша. – Тебе нужно подготовить трёхлитровые банки, то есть банки, в которые поместится 3 литра сока. Правильно?
– Да! – ответил Саша.
– Всего вы собрали 27 литров берёзового сока, – продолжил рассуждать Паша.
– Всё верно! – подтвердил Саша.
– Хорошо! – продолжил Паша. – Значит, надо найти такое число, которое при умножении на 3 даст 27.
– Так это же легко, – сказал Саша. – Если 9 умножить на 3, то получится 27.
– Значит, тебе нужно подготовить 9 банок! – закончил Паша.

– И что, каждый раз так делают? – поинтересовался Саша. – Если в жизни встретятся подобные задачки, нужно будет искать число, которое при умножении с известным числом даёт нужное число?
– Не знаю! – задумался Паша. – А давай спросим у Электроши.
– Ребята, прежде чем я вам расскажу, как решать подобные задачки, давайте немного разомнёмся и выполним устные задания, – предложил Электроша.

– Давайте сверимся! Посмотрите, что у вас должно было получиться!
– А теперь вернёмся к вашему вопросу, – предложил Электроша. – Вы всё правильно посчитали и верно заметили, что для того, чтобы узнать, сколько нужно подготовить трёхлитровых банок, нужно найти такое число, которое при умножении на 3 даст 27. То есть вы по одному из множителей и заданному произведению нашли второй множитель. В таких случаях говорят о делении.

– Запомните! – сказал Электроша. – Действие, с помощью которого по произведению и одному из множителей находят другой множитель, называют делением. Действие деления определяют с помощью действия умножения. Например, 27 разделить на 3 – значит найти такое число, которое при умножении на 3 даёт число 27. Имеем: 9 умножить на 3 равно 27, поэтому 27 разделить на 3 равно 9.

Вообще, для натуральных чисел
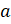 ,
, 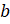 и
и 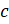 равенство
равенство 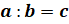 верно, если верно равенство
верно, если верно равенство 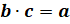 .
.
В равенстве 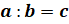 число
число 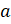 называют делимым, число
называют делимым, число 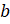 – делителем, число
– делителем, число 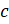 и саму запись
и саму запись 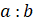 – частным.
– частным.
Частное 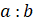 показывает, во сколько раз число
показывает, во сколько раз число 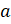 больше числа
больше числа 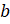 или во сколько раз число
или во сколько раз число 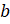 меньше числа
меньше числа 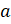 .
.

– Электроша, а я слышал, что на 0 делить нельзя, – перебил Паша. – Это правда?
– Давайте порассуждаем, – предложил Электроша. – Возьмём какое-нибудь число, например 7. Что значит разделить 7 на 0?
– Это значит найти такое число
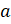 , которое при умножении на 0 даёт 7, – предположил Саша.
, которое при умножении на 0 даёт 7, – предположил Саша.
– Но ведь мы знаем, что если любое число умножить на 0, то всегда получится 0, – возмутился Паша.
– Верно! – подтвердил Электроша. – И это нам говорит, что никакое натуральное число невозможно разделить на 0. Следовательно, вычислить частное 7 и 0 нельзя.

Запомните! На нуль делить нельзя.

– Электроша, а 0 можно разделить на какое-нибудь число? – поинтересовался Саша.
– Давайте опять порассуждаем, – предложил Электроша. – Что значит разделить 0 на число
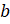 ?
?
– Это значит найти такое число
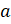 , которое при умножении на
, которое при умножении на 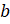 даст 0, – предположил Паша.
даст 0, – предположил Паша.
– Хорошо! – согласился Электроша.
– Тогда скажите, можно ли найти такое число 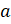 ?
?
– Так это всем понятно, что можно, – начал
Саша. – Сюда подойдёт число 0. Ведь 0 умножить на 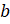 равно 0.
равно 0.

– Молодец! – похвалил Сашу Электроша. – Запомните! При делении нуля на
натуральное число частное равно нулю. Также для любого натурального числа 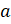 верны следующие равенства:
верны следующие равенства: 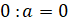 ,
, 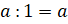 ,
, 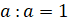 . Первое равенство говорит, что деление числа
на единицу результатом имеет само число. Второе – деление числа на само себя
имеет результатом число один. Последнее равенство выполняется при всех
натуральных числах, кроме
. Первое равенство говорит, что деление числа
на единицу результатом имеет само число. Второе – деление числа на само себя
имеет результатом число один. Последнее равенство выполняется при всех
натуральных числах, кроме 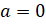 , так как на ноль делить нельзя.
, так как на ноль делить нельзя.

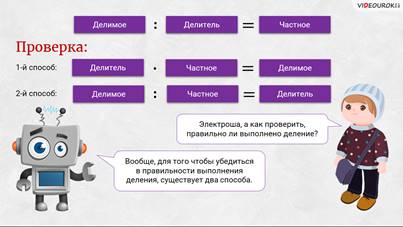
– Электроша, а как проверить, правильно ли выполнено деление? – спросил Паша.
– Вообще, для того чтобы убедиться в правильности выполнения деления, существует два способа, – сказал Электроша. – Первый способ: нужно перемножить делитель и частное, в результате должно получиться делимое. Второй способ: нужно разделить делимое на частное, в результате должен получиться делитель.
– А теперь давайте попробуем найти частное от деления чисел 126 126 и 231.
– Ого! Какие большие числа! – удивились ребята. – Тут нам без калькулятора не обойтись.
– Ребята, всё гораздо проще, чем кажется на первый взгляд, – успокоил ребят Электроша. – Вы уже умеете делить уголком многозначное число на двузначное. Точно так же выполняют и деление любых многозначных чисел. Такой способ поможет быстро и без ошибок выполнить вычисление.
– Итак, запишем числа рядом на одной строчке, а чтобы их не перепутать, поставим между ними уголок. Под горизонтальной чертой будем писать частное или результат деления. Приступим к делению. В данном случае, чтобы найти первую цифру частного, надо взять первые четыре цифры делимого и получившееся число разделить на делитель 231.
– Электроша, а почему мы берём именно первые четыре цифры делимого? – спросил Саша.
– Потому что если бы мы взяли хотя бы на одну цифру меньше, то получившееся число, в данном случае 126, оказалось бы меньше делителя 231, а такое деление мы не можем выполнить.
Итак, берём первые четыре цифры делимого и попытаемся разделить получившееся число на 231. Наиболее подходящим здесь будет число 5. Запишем его в строчке под делителем. Затем 5 умножим на 231. Получим 1155. Получившееся число запишем под нашими четырьмя цифрами, что мы брали в качестве делимого. Теперь от 1261 отнимем 1155. Получим 106. Число 106 меньше делителя, значит, число 5 мы нашли верно. Теперь снесём следующую цифру делимого, то есть 2. Разделим число 1062 на 231. Возьмём по 4. Запишем четвёрку рядом с пятёркой в частном. Затем 4 умножим на 231. Получим 924. И вычтем из 1062 число 924. Получим 138. Видим: это число меньше делителя, значит, число 4 мы нашли верно. Затем снесём последнюю цифру делимого. Получившееся число 1386 разделим на 231. Берём по 6. 6 умножим на делитель и получим 1386. Выполним вычитание. Получим 0. Деление закончено. Следовательно, 126 126 разделить на 231 равно 546.

– А теперь давайте решим несколько уравнений: 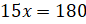 ,
, 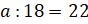 ,
, 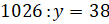 – предложил Электроша.
Итак, первое уравнение
– предложил Электроша.
Итак, первое уравнение 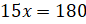 .
.
– Для того чтобы найти корень этого
уравнения, нужно вспомнить правило нахождения неизвестного множителя, – начал
Саша. – Чтобы найти неизвестный множитель, надо произведение разделить на
известный множитель. Получаем, что 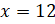 .
.
– Молодец! – похвалил Сашу Электроша. – Следующее уравнение 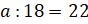 .
.
– А здесь
нам нужно воспользоваться правилом нахождения неизвестного делимого, – сказал Паша, – чтобы найти неизвестное
делимое, надо делитель умножить на частное. Тогда получаем, что
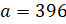 .
.
– Правильно! – подтвердил Электроша.
– И осталось решить последнее уравнение: 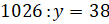 .
.
– В этом уравнении нам нужно найти делитель,
– начал рассуждать Cаша, – значит, воспользуемся правилом нахождения неизвестного делителя:
чтобы найти неизвестный делитель, надо делимое разделить на частное. Получаем, что 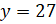 .
.

– А теперь, ребята, давайте посмотрим, как вы всё поняли, и выполним несколько заданий.
Задание первое: скорость моторной лодки 28 км/ч, а скорость течения реки в 14 раз меньше. Какое расстояние по течению реки пройдёт лодка за 4 часа?
Решение: сначала найдём скорость течения реки. Для этого 28 разделим на 14. Получим, что скорость течения реки 2 км/ч. Затем вычислим скорость моторной лодки по течению реки. Для этого к скорости моторной лодки прибавим скорость течения реки. Получим 30 км/ч. И осталось узнать, какое расстояние пройдёт моторная лодка по течению реки за 4 часа. 30 умножим на 4. Получаем, что моторная лодка за 4 часа пройдёт 120 км по течению реки.

Следующее задание: из двух городов, расстояние между которыми 260 км, одновременно вышли два поезда в одном направлении. Скорость шедшего впереди поезда 50 км/ч, а скорость шедшего позади поезда 70 км/ч. Через сколько часов после выхода второй поезд догонит первый?
Решение: для начала вычислим, на сколько уменьшается расстояние между поездами каждый час. Для этого от 70 отнимем 50. Получим 20. А затем вычислим время, за которое второй поезд догонит первый. 260 разделим на 20. Получаем, что второй поезд догонит первый поезд через 13 часов.


 Получите свидетельство
Получите свидетельство Вход
Вход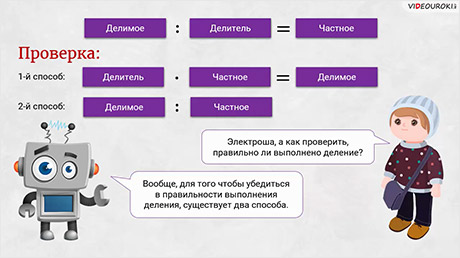



 0
0 2181
2181

