Материал урока.
На прошлых занятиях мы ввели понятие вектора в пространстве.
Отрезок, для которого указано, какой из его концов является началом, а какой — концом, называется вектором. Любая точка пространства также является вектором, нулевым вектором.
Мы
выяснили, что длина ненулевого вектора 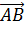 равна длине
отрезка AB. А длина нулевого
вектора равна 0.
равна длине
отрезка AB. А длина нулевого
вектора равна 0.
Так же дали определение коллинеарным векторам. Это векторы, которые лежат на одной прямой или на параллельных прямых.
Если коллинеарные векторы имеют одинаковое направление, то они являются сонаправленными. Если же их направления противоположны, то векторы называют противоположно направленными.
На этом уроке мы будем говорить о равных векторах. Определение равных векторов в пространстве звучит так же, как и определение равных векторов на плоскости.
Равными называют сонаправленные векторы, длины которых равны.
Ну, а противоположно направленные векторы, длины которых равны, называют противоположными.
Рассмотрим пример.
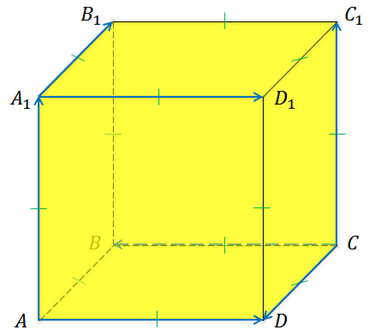
На рисунке изображён куб ABCDA1B1C1D1. Среди векторов, показанных на рисунке, найдём пары равных и противоположных векторов.
Перед нами куб, и стоит вспомнить, что это за фигура. Это многогранник, все грани которого являются квадратами. Значит, все рёбра куба равны между собой.
Векторы
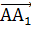 и
и 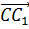 коллинеарны.
Ведь понятно, что ребра AA1
и DD1
параллельны, как противоположные стороны квадрата. Аналогично, параллельны
рёбра DD1
и CC1.
А значит, параллельны рёбра АА1 и CC1.
Так же по рисунку понятно, что данные векторы сонаправлены, а их длины по
условию равны. Тогда векторы
коллинеарны.
Ведь понятно, что ребра AA1
и DD1
параллельны, как противоположные стороны квадрата. Аналогично, параллельны
рёбра DD1
и CC1.
А значит, параллельны рёбра АА1 и CC1.
Так же по рисунку понятно, что данные векторы сонаправлены, а их длины по
условию равны. Тогда векторы 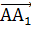 и
и 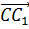 равны.
равны.
Векторы
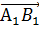 и
и 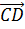 равны по длине,
но противоположно направлены. Значит, эти векторы являются противоположными.
равны по длине,
но противоположно направлены. Значит, эти векторы являются противоположными.
Векторы
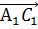 и
и
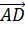 равны
по длине и сонаправлены, а значит, равны.
равны
по длине и сонаправлены, а значит, равны.
Векторы
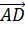 и
и 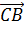 равны
по длине и противоположно направлены, а значит, противоположны.
равны
по длине и противоположно направлены, а значит, противоположны.
Также
противоположно направленными и равными по длине будут векторы 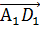 и
и 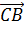 . Они являются
противоположными.
. Они являются
противоположными.
Так мы с вами выписали две пары равных векторов и три пары противоположных векторов.
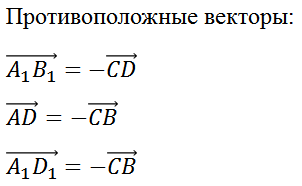
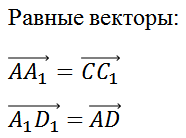
Задача.
 правильный
тетраэдр.
правильный
тетраэдр.
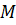 ,
, 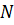 ,
, 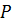 и
и 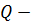 середины рёбер
середины рёбер 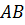 ,
, 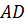 ,
, 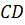 и
и 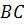 .
.
1. Среди изображённых векторов указать пары равных векторов.
2.
Установить вид четырёхугольника 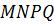 .
.
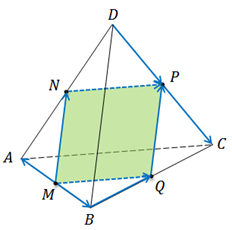
Решение.
Равными являются сонаправленные векторы, длины которых равны.
А для того чтобы векторы были сонаправлены, они должны быть коллинеарны. То есть должны лежать на параллельных прямых или на одной прямой.
Никакие
рёбра тетраэдра не являются параллельными. Поэтому на рёбрах будем искать
векторы, лежащие на одной прямой. Такими являются векторы 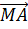 и
и
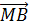 , а также
, а также 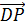 и
и
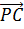 . Точки P
и М являются серединами соответствующих рёбер. Значит, равны длины векторов
. Точки P
и М являются серединами соответствующих рёбер. Значит, равны длины векторов 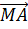 и
и
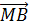 , а также
, а также 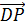 и
и
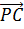 .
.
Но
векторы 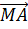 и
и
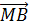 противоположно
направлены, а вот векторы
противоположно
направлены, а вот векторы 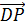 и
и
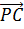 — сонаправлены.
— сонаправлены.
Так
мы нашли одну пару равных векторов, 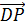 и
и
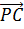 .
.
Далее рассмотрим треугольник ABD. Точки М и N — середины сторон AB и AD. Значит, МN — средняя линия. И она параллельна стороне BD, а также равна её половине.
В треугольнике CBD отрезок PQ является средней линией. Он параллелен стороне BD и равен её половине.
Так
мы получаем, что отрезки МN
и PQ параллельны и равны. Значит, векторы
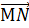 и
и 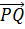 коллинеарны и,
очевидно, сонаправлены. И так как равны их длины, то можно сказать, что эти
векторы равны.
коллинеарны и,
очевидно, сонаправлены. И так как равны их длины, то можно сказать, что эти
векторы равны.
Аналогично, в треугольнике ADC отрезок NP является средней линией. Он параллелен стороне AC и равен её половине.
В треугольнике ABC отрезок MQ также является средней линией. Он параллелен стороне AC и равен её половине.
Отсюда
получаем, что отрезки NP
и MQ параллельны и равны. А значит,
можем сделать вывод о равенстве векторов 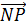 и
и 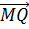 .
.
Так мы с вами нашли три пары равных векторов.
Теперь осталось определить вид четырёхугольника MNPQ.
Нами уже установлено, что противоположные стороны этого четырёхугольника параллельны и равны. А это говорит о том, что данный четырёхугольник является параллелограммом.
Но так как все рёбра данного тетраэдра равны, то равны и длины средних линий, рассматриваемых ранее треугольников.
Получаем, что MNPQ — параллелограм, все стороны которого равны между собой. А значит, данный четырёхугольник является ромбом.
Ответ.
1) 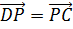 ,
, 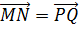 ,
, 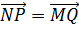 ; 2)
; 2) 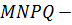 ромб.
ромб.
Далее вспомним, что от любой точки плоскости можно отложить вектор равный данному, и притом только один.
Это утверждение верно и для любой точки пространства.
Действительно,
если рассмотреть некоторый вектор 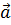 и
произвольную точку пространства М. Через точки начала и конца данного вектора,
а также через точку М можно провести плоскость.
и
произвольную точку пространства М. Через точки начала и конца данного вектора,
а также через точку М можно провести плоскость.
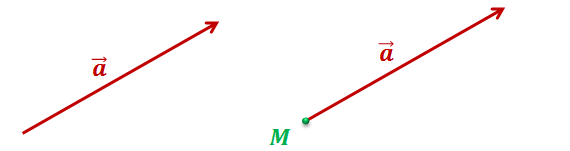
В
полученной плоскости отложим от точки М вектор 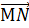 равный вектору
равный вектору 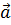 . Очевидно, он
искомый. А из построений понятно, что он будет единственным. Ведь первая
аксиома стереометрии говорит, что через 3 точки пространства можно провести
только 1 плоскость.
. Очевидно, он
искомый. А из построений понятно, что он будет единственным. Ведь первая
аксиома стереометрии говорит, что через 3 точки пространства можно провести
только 1 плоскость.
Говорят
«вектор 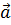 отложен от
точки М».
отложен от
точки М».
Выполним задание.
В параллелепипеде ABCDA1B1C1D1 точки K и М — середины сторон A1D1 и B1C1 соответственно. Стоит напомнить, что все грани параллелепипеда являются параллелограммами, а их противоположные стороны равны. Значит, равны и их половины.
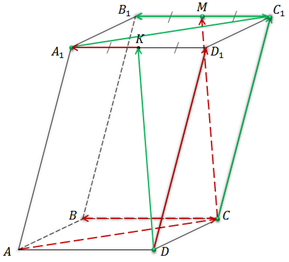
Итак, нам нужно назвать векторы, которые получатся, если от данной точки отложить вектор, равный данному.
Первым
нам нужно назвать вектор, который получится, если от точки C
отложить вектор, равный вектору 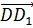 .
.
Нам известно, что от точки пространства можно отложить только один вектор, равный данному.
Вектор
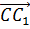 отложен от
точки C и он равен вектору
отложен от
точки C и он равен вектору 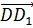 . Значит, вектор
. Значит, вектор
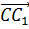 искомый.
искомый.
Далее
назовём вектор, который получится, если от точки D
отложить вектор, равный вектору 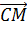 .
.
Вектор
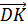 отложен от
точки D и равен вектору
отложен от
точки D и равен вектору 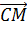 . Значит, он и
является искомым.
. Значит, он и
является искомым.
Так,
если от точки А1 отложить вектор, равный вектору 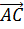 , то мы получим
вектор
, то мы получим
вектор 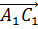 .
.
Если
же от точки C1
отложить вектор, равный вектору 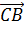 , то мы получим
вектор
, то мы получим
вектор 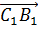 .
.
И,
отложив от точки М вектор, равный вектору 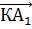 , мы получим
вектор
, мы получим
вектор 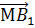 .
.
Подведём итоги урока.
На этом уроке мы выяснили, что, так же как и на плоскости, в пространстве равными называют сонаправленные векторы, длины которых равны.
Если же векторы противоположно направлены и их длины равны, то такие векторы называют противоположными.
Так же мы отметили, что от любой точки пространства можно отложить вектор, равный данному вектору, и притом только один.
Всем этим знаниям мы нашли применение при решении задач.

 Получите свидетельство
Получите свидетельство Вход
Вход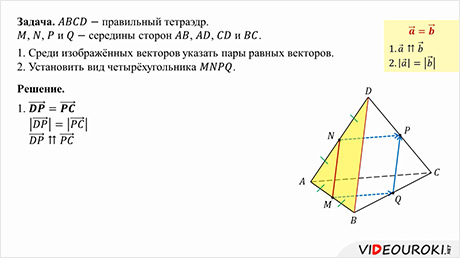



 0
0 5149
5149

