Сложение и вычитание векторов

Материал урока.

Вспомним, как мы вводили понятие суммы двух векторов в планиметрии.

Сначала мы рассматривали такой пример.

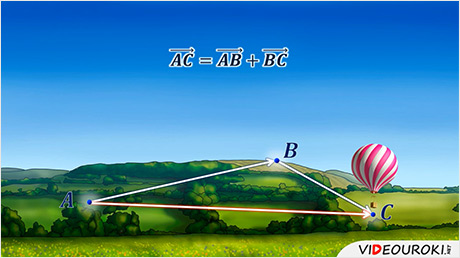
Под действием воздушных масс воздушный шар сначала двигался из точки А в точку B, а затем из точки B переместился в точку C.

Каждое из этих двух перемещений можно представить в виде вектора.  и .

Но можно ведь сказать, что в результате воздушный шар из точки А попал в точку C. И это перемещение задает вектор .

Так как перемещение из точки А в C складывается из перемещений из точки А в B и из B в C, то можно записать, что вектор .

Этот пример подводит нас к понятию суммы двух векторов.

Рассмотрим два ненулевых вектора:  и .

Отметим произвольную точку А и отложим от неё вектор , равный вектору . Далее от точки B отложим вектор , равный вектору .

Можем изобразить вектор , который называется суммой векторов  и .

Данное правило сложения векторов в пространстве, так же, как и в планиметрии, будем называть правилом треугольника.

Нужно отметить, что сумма векторов  и  не зависит от выбора точки А, от которой будет отложен вектор .

Докажем это.

Найдём сумму векторов  и , но начнём откладывать их от некоторой точки А₁.

Нам необходимо доказать, что полученный вектор  равен вектору .

Из построений очевидно, что векторы  и  равны. А значит, они сонаправлены и равны по длине. То есть стороны AB и A₁B₁ четырёхугольника ABB₁A₁ параллельны и равны. И этот четырёхугольник является параллелограммом.

Стороны AA₁ и  BB₁ данного параллелограмма также равны и параллельны. Тогда получаем, равны векторы  и .

Аналогично, из равенства векторов  и  следует, что четырёхугольник BCC₁B₁ также является параллелограммом. А значит, равны векторы  и .

Из полученных равенств получаем, что равны векторы  и .

Поэтому четырёхугольник AA₁C₁C — параллелограмм. Его стороны AC и A₁C₁ параллельны и равны. А значит, равны векторы  и .

Что и требовалось доказать.

Итак, в точности так же, как и на плоскости, мы ввели правило треугольника сложения двух векторов в пространстве. И доказали, что сумма векторов  и  не зависит от выбора точки А, от которой будет отложен вектор .

Для любых трёх точек пространства А, B и C правило треугольника можно сформулировать так: сумма векторов  и  равна вектору .

То есть даже не строя вектор суммы можно его найти. Если конец вектора, являющегося первым слагаемым, совпадаем с началом вектора, являющегося вторым слагаемым, то началом вектора суммы является начало первого вектора, а концом — конец второго вектора.

Так же для сложения двух векторов можно применять правило параллелограмма, которое мы уже формулировали в планиметрии. Вспомним его. От произвольной точки А отложим векторы  и , равные векторам  и соответственно.

Теперь на этих векторах построим параллелограмм ABCD. Вектор  является вектором суммы векторов  и .

Для любых векторов ,  и  действуют переместительный и сочетательный законы сложения векторов.

Эти законы мы уже записывали и доказывали для векторов на плоскости.

Выполним задание.

На экране изображён параллелепипед ABCDA₁B₁C₁D₁.

Требуется назвать векторы, начало и конец которых совпадают с вершинами параллелепипеда, и которые равны соответствующей сумме векторов.

Первой рассмотрим сумму векторов  и

Чтобы сложить векторы по правилу треугольника, они должны быть отложены друг за другом, а чтобы воспользоваться правилом параллелограмма, они должны быть отложены от одной точки.

Данные векторы не подходят ни к одному правилу.

Но здесь нам поможет знание о том, что от любой точки пространства можно отложить вектор равный данному, и притом только один.

Так как перед нами параллелепипед и все его грани являются параллелограммами, то можно сказать, что есть вектор, который отложен от точки А и равен вектору  Напомним, что равными называются сонаправленные векторы, длины которых равны.

Вектор Ведь эти векторы лежат на противоположных сторонах параллелограмма, которые равны и параллельны.

От данной нам суммы перейдём к сумме векторов  и . Они отложены от одной точки, поэтому воспользуемся правилом параллелограмма. Если построить параллелограмм на этих векторах, то мы получим грань ABCD.

Диагональ AC и будет вектором суммы данных векторов.

Следующей рассмотрим сумму векторов  и .

Они уже отложены от одной точки, и на этих векторах можно построить параллелограмм ABC₁D₁. Диагональ AC₁ и будет являться вектором суммы.

Далее рассмотрим сумму векторов  и .

Вектор равен вектору . И перейдя к сумме векторов  и , не трудно заметить, что они отложены друг за другом, и именно поэтому можно применить правило треугольника. Вектор  — искомый.

Обратите внимание, пользуясь переместительным законом, можно записать, что сумма векторов  и ,  равна сумме векторов ,  и . Тогда по правилу треугольника сложения векторов для трёх произвольных точек пространства, можно сразу записать вектор суммы — . Так мы получили тот же вектор.

Теперь рассмотрим сумму векторов  и . Вектор  равен вектору . Векторы полученной суммы отложены друг за другом, поэтому вектором их суммы будет вектор .

Последней рассмотрим сумму векторов  и . Видим, что конец первого вектора в сумме совпадает с началом второго вектора. Тогда можно сразу сказать, что вектором суммы является вектор . Этот же результат мы получим, пользуясь рисунком.

Далее поговорим о разности векторов  и . Это такой вектор, сумма которого с вектором  равна вектору .

Проиллюстрируем это определение для данных векторов  и .

Итак, вектор должен являться суммой векторов  и . Тогда, отложив вектор  от начала вектора , мы без труда проведём вектор  из конца вектора  к концу вектора .

Действительно,  плюс  равно . А значит, вектор  равен разности векторов  и .

Таким образом, можно откладывать векторы уменьшаемое и вычитаемое от одной точки, а вектором разности будет являться вектор, направленный из конца вектора вычитаемого к концу вектора уменьшаемого.

Вы помните, что векторы называются противоположными, если их длины равны, а направления противоположны

Так вот если в данной иллюстрации у вектора  сменить направление, то есть заменить его на «», то мы получим, что вектор  равен разности векторов  и , а также, по правилу треугольника, сумме векторов  и «».

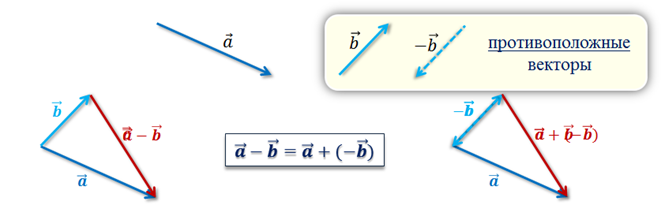
Так мы получили два способа построения вектора разности.

Рассмотрим тот же параллелепипед, что и в предыдущей задаче.

Нужно назвать векторы, начало и конец которых совпадают с вершинами параллелепипеда, и которые равны соответствующей разности векторов.

Найдём вектор разности векторов  и .

Они отложены от одной точки, поэтому вектором разности будет являться вектор, направленный из конца вектора-вычитаемого  к концу вектора-уменьшаемого . Так получаем вектор .

Применим второй способ построения вектора разности.

Нам известно, что разность векторов можно представить в виде суммы вектора уменьшаемого и вектора, противоположного вектору вычитаемому. Вектором противоположным вектору  является вектор . По правилу треугольника сложения двух векторов мы также получим вектор .

Далее рассмотрим разность векторов  и .

Они отложены от одной точки. и поэтому вектор разности будет направлен из конца вектора-вычитаемого  к концу вектора-уменьшаемого . Таким образом мы получим вектор .

Последней рассмотрим разность векторов  и . Вектор  заменим равным ему вектором . А разностью векторов  и  будет вектор . В результате и разность векторов  и  равна вектору .

Подведём итоги нашего урока.

В точности так же, как и на плоскости, на этом уроке мы с вами сформулировали правило треугольника и правило параллелограмма сложения двух векторов в пространстве, а также записали переместительный и сочетательный законы сложения векторов.

Убедившись в том, что разность векторов  и  равна сумме вектора  и вектора, противоположного вектору , мы получили два способа построения вектора разности двух векторов.

Так мы рассмотрели сложение и вычитание векторов в пространстве.