Материал урока.
Вам уже известны правила сложения и вычитания двух векторов.
Чтобы
сложить два неколлинеарных вектора  и
и
 по
правилу треугольника, нужно от некоторой точки А отложить вектор
по
правилу треугольника, нужно от некоторой точки А отложить вектор  ,
равный вектору
,
равный вектору  .
Далее от точки B отложить вектор
.
Далее от точки B отложить вектор
 ,
равный вектору
,
равный вектору  .
Вектор
.
Вектор  является
вектором суммы двух векторов
является
вектором суммы двух векторов  и
и
 .
.
Чтобы
сложить два вектора по правилу параллелограмма, нужно отложить от произвольной
точки А векторы  и
и
 ,
равные векторам
,
равные векторам  и
и
 соответственно,
и построить на них параллелограмм ABCD.
Тогда вектор
соответственно,
и построить на них параллелограмм ABCD.
Тогда вектор  равен
сумме векторов
равен
сумме векторов  и
и
 .
.
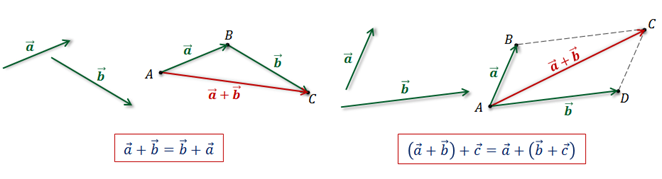
Также вам уже знакомы законы сложения векторов: переместительный и сочетательный.
Ну,
а убедившись в том, что разность векторов  и
и
 равна
сумме вектора
равна
сумме вектора  и
вектора, противоположного вектору
и
вектора, противоположного вектору  ,
мы получили два способа построения вектора разности двух векторов.
,
мы получили два способа построения вектора разности двух векторов.
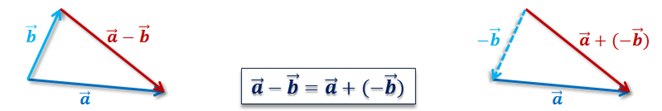
Сегодня мы будем учиться складывать несколько векторов в пространстве. Но сначала вспомним, как мы это делали на плоскости.
Построим
вектор суммы векторов  ,
,
 и
и
 .
.
От
некоторой точки А отложим вектор  ,
равный вектору
,
равный вектору  .
Далее от точки B отложим вектор
.
Далее от точки B отложим вектор  ,
равный вектору
,
равный вектору  .
А от точки C отложим вектор
.
А от точки C отложим вектор  ,
равный вектору
,
равный вектору  .
.
Будем последовательно складывать наши векторы, пользуясь правилом треугольника.
Сумма
векторов  и
и
 равна
вектору
равна
вектору  .
.
Теперь
к вектору  добавим
вектор
добавим
вектор  .
В результате мы получаем вектор
.
В результате мы получаем вектор  .
.
Тогда
можем сказать, что сумма векторов  ,
,
 и
и
 .
равна вектору
.
равна вектору  .
.
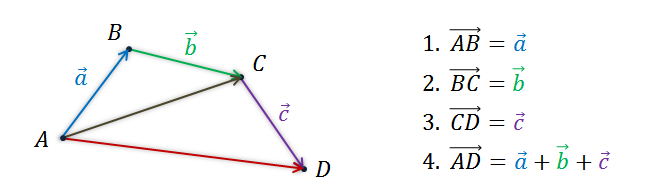
Так, последовательно складывая первый вектор со вторым, затем их сумму с третьим и так далее, можно найти суммы четырёх, пяти и большего числа векторов.
Такое правило построения суммы векторов называют правилом многоугольника, и оно позволяет построить вектор суммы неограниченного количества векторов.
Задача. Построить
вектор суммы попарно неколлинеарных векторов  ,
,
 ,
,
 ,
,
 и
и
 .
.

Построение.

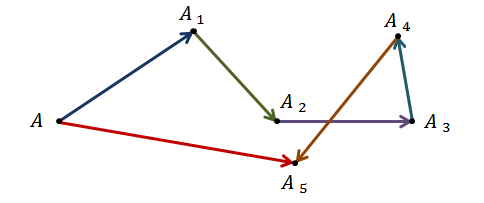

Примеры, приведённые нами, подходят для векторов, лежащих в одной плоскости. А мы, изучая стереометрию, находимся в пространстве, поэтому правило многоугольника сложения векторов в пространстве может иметь и другую иллюстрацию.
Задача.
Рассмотрим векторы  ,
,
 и
и
 ,
такие, что
,
такие, что  ,
,
 лежат
в одной плоскости, а вектор
лежат
в одной плоскости, а вектор  не
лежит в этой плоскости. Найдём сумму этих векторов.
не
лежит в этой плоскости. Найдём сумму этих векторов.

Решение.
Выберем
любую удобную точку О в пространстве и отложим от неё вектор  ,
равный вектору
,
равный вектору  ,
а от точки А отложим вектор
,
а от точки А отложим вектор  ,
равный вектору
,
равный вектору  .
Понятно, что через проведённые векторы можно провести плоскости. Далее, от
точки B отложим вектор
.
Понятно, что через проведённые векторы можно провести плоскости. Далее, от
точки B отложим вектор  ,
равный вектору
,
равный вектору  .
Вектором суммы данных векторов является вектор
.
Вектором суммы данных векторов является вектор  .
.
Вы видите, что многоугольник сложения в данном случае является пространственным, то есть не все его вершины лежат в одной плоскости.
Сформулируем правило многоугольника для произвольных точек пространства А1, А2 ,…, Аn.


Это равенство справедливо для любых точек А1, А2, …, An. И, в частности, для случая, когда некоторые из них совпадают.
Например,
если начало первого вектора совпадает с концом последнего, то сумма данных
векторов равна  .
.
Задача. Упростить выражения
Выполним задание, где, пользуясь данной формулировкой, упростим выражения.
а)

б)

в)


г)
 =
=

Так мы с вами рассмотрели примеры преобразования выражений с векторами, представленных в виде алгебраической суммы.
Задача.
 ,
,
 ,
,
 ,
,
 произвольные
точки пространства.
произвольные
точки пространства.
Представить
вектор  в
виде алгебраической суммы векторов:
в
виде алгебраической суммы векторов:
а)
 ,
,
 ,
,
 б)
б)  ,
,
 ,
,
 в)
в)  ,
,
 ,
,

Решение.
 В
последнем задании рассмотрим параллелепипед ABCDA1B1C1D1.
В
последнем задании рассмотрим параллелепипед ABCDA1B1C1D1.

Нужно
указать вектор  ,
начало и конец которого являются вершинами параллелепипеда. И чтобы истинными
были данные равенства.
,
начало и конец которого являются вершинами параллелепипеда. И чтобы истинными
были данные равенства.
Сумма
векторов  .
.
По
рисунку понятно, чтобы восстановить правило многоугольника, не достает вектора  .
Значит, вектор
.
Значит, вектор  .
.
Далее
рассмотрим выражение, где сумма векторов  .
.

По
рисунку понятно, что сумма известных векторов из левой части равенства равна
вектору  .
И чтобы вся сумма равнялась вектору
.
И чтобы вся сумма равнялась вектору  ,
вектор
,
вектор  должен
быть равен вектору
должен
быть равен вектору  .
.
Перейдём
к следующему равенству. 

Чтобы
восстановить правило многоугольника, вектор  удобнее
заменить равным ему вектором
удобнее
заменить равным ему вектором  .
Тогда становится понятно, что вектор «-
.
Тогда становится понятно, что вектор «- »
равен вектору
»
равен вектору  .
А вектор
.
А вектор  отсюда
равен вектору
отсюда
равен вектору  .
.
Разберёмся
с последним равенством.  .
.

Левую
часть представим в виде суммы и заменим вектор «–  »
на
»
на  .
.
Изобразим
данные векторы. Видим, что искомый вектор  равен
вектору
равен
вектору  .
.
Подведём итоги урока.
Сегодня мы сформулировали правило многоугольника сложения нескольких векторов в пространстве. И нашли его отличие от того же правила на плоскости.
Оно заключается в том, что полученный многоугольник может являться пространственным, то есть не все его вершины лежат в одной плоскости.
Также мы сформулировали правило многоугольника для произвольных точек пространства А1, А2 …, Аn.
Сумма
векторов  +
+
 ,+
,+ =
=
 ,.
,.
И
если начало первого вектора совпадает с концом последнего, то сумма данных
векторов равна  .
.
Эти знания мы смогли применить при выполнении заданий.

 Получите свидетельство
Получите свидетельство Вход
Вход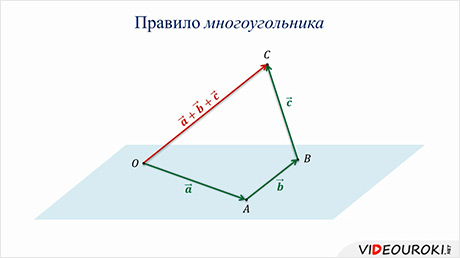



 0
0 8976
8976

