Материал урока.
Вам уже знакомы правило треугольника, правило параллелограмма и правило многоугольника сложения векторов.
Чтобы
сложить неколлинеарные векторы  и
и
 по
правилу треугольника, нужно от некоторой точки А отложить вектор
по
правилу треугольника, нужно от некоторой точки А отложить вектор  ,
равный вектору
,
равный вектору  .
Далее от точки B отложить вектор
.
Далее от точки B отложить вектор
 ,
равный вектору
,
равный вектору  .
Вектор
.
Вектор  является
вектором суммы двух векторов
является
вектором суммы двух векторов  и
и
 .
.
Для
сложения этих же векторов можно использовать правило параллелограмма. При этом
нужно отложить от произвольной точки А векторы  и
и
 ,
равные векторам
,
равные векторам  и
и
 соответственно,
и построить на них параллелограмм ABCD.
Тогда вектор
соответственно,
и построить на них параллелограмм ABCD.
Тогда вектор  равен
сумме векторов
равен
сумме векторов  и
и
 .
.
Для сложения нескольких векторов применяют правило многоугольника. При этом от некоторой точки последовательно откладывают векторы друг за другом, и вектором их суммы является вектор, проведённый от начала первого вектора к концу последнего. Причём полученный многоугольник может быть не только плоским, но и пространственным.

Также вы владеете двумя способами построения вектора разности.
Можно
от некоторой точки О отложить векторы  и
и
 ,
равные векторам
,
равные векторам  и
и
 .
При этом вектором их разности будет вектор
.
При этом вектором их разности будет вектор  ,
направленный от конца вектора-вычитаемого к концу вектора-уменьшаемого.
,
направленный от конца вектора-вычитаемого к концу вектора-уменьшаемого.
Так
же, пользуясь теоремой о разности двух векторов, разность векторов  и
и
 можно
представить в виде суммы вектора
можно
представить в виде суммы вектора  и
вектора, противоположного вектору
и
вектора, противоположного вектору  .
.
Тогда,
отложив от некоторой точки О вектор  ,
равный вектору
,
равный вектору  ,
а от точки А — вектор
,
а от точки А — вектор  ,
равный вектору «-
,
равный вектору «-  »,
по правилу треугольника получим вектор
»,
по правилу треугольника получим вектор  .
.
Он
является вектором суммы вектора  и
вектора, противоположного вектору
и
вектора, противоположного вектору  .
И, соответственно, вектором разности векторов
.
И, соответственно, вектором разности векторов  и
и
 .
.

Как и на плоскости в пространстве вектор можно умножать на число. На этом-то уроке мы и поговорим об умножении вектора на число в пространстве.
Рассмотрим пример, который поможет нам вспомнить, что представляет собой произведение вектора на число.

Парусник дрейфует прямолинейно с одной и той же скоростью, а один из лайнеров движется в попутном направлении со скоростью в пять раз большей. Второй лайнер движется им на встречу, то есть в противоположном направлении, с той же скоростью, что и первый лайнер.
Если
изобразить скорость парусника вектором  ,
то скорость первого лайнера, движущегося в попутном направлении, нужно
изобразить в виде сонаправленного вектора, длина которого в пять раз больше. И
выразить эту скорость можно через скорость
,
то скорость первого лайнера, движущегося в попутном направлении, нужно
изобразить в виде сонаправленного вектора, длина которого в пять раз больше. И
выразить эту скорость можно через скорость  умножением
на 5.
умножением
на 5.
Вектор
скорости второго лайнера должен иметь такую же длину, как и вектор скорости
первого лайнера, но он должен быть ему противоположно направленным. Значит, его
можно выразить через вектор  умножением
на -5.
умножением
на -5.
Определение.
Произведением ненулевого вектора  на
число k называется такой
вектор
на
число k называется такой
вектор  ,
длина которого равна произведению модуля числа k
и длины данного вектора
,
длина которого равна произведению модуля числа k
и длины данного вектора  .
Причем векторы
.
Причем векторы  и
и
 сонаправлены,
если k
сонаправлены,
если k ,
и противоположно направлены, если k<0.
,
и противоположно направлены, если k<0.
Произведение
числа k на вектор  в
пространстве обозначают так же как и на плоскости.
в
пространстве обозначают так же как и на плоскости.

Имеют место такие следствия из определения.

Действительно,
по определению длина этого вектора равна произведению длины вектора  на
0, то есть равна 0. Значит, получаем нулевой вектор.
на
0, то есть равна 0. Значит, получаем нулевой вектор.
Вторым следствием из определения является то, что ненулевой
вектор  коллинеарен вектору, заданному произведением данного вектора
коллинеарен вектору, заданному произведением данного вектора  на число k.
на число k.

Ведь, если k≥0, то полученный вектор сонаправлен вектору  , а если k<0, то он противоположно направлен ему. Но в каждом из этих
случаев они будут коллинеарны.
, а если k<0, то он противоположно направлен ему. Но в каждом из этих
случаев они будут коллинеарны.
Свойства умножения вектора на число, известные нам из планиметрии, имеют место и для векторов в пространстве. Напомним их.
Чтобы умножить вектор  на произведение чисел k и l, можно вектор
на произведение чисел k и l, можно вектор  сначала умножить на число l, а затем на число k. Этот закон называют сочетательным,
и его можно проиллюстрировать так.
сначала умножить на число l, а затем на число k. Этот закон называют сочетательным,
и его можно проиллюстрировать так.

Вторым
свойством запишем, что произведение вектора  на
сумму чисел k и l
равно сумме произведений «вектора
на
сумму чисел k и l
равно сумме произведений «вектора  на
число k» и «вектора
на
число k» и «вектора  на
число l». Это первый
распределительный закон.
на
число l». Это первый
распределительный закон.

Запишем второй распределительный закон.
Произведение
суммы векторов  и
и
 на
число k равно сумме
произведений «вектора
на
число k равно сумме
произведений «вектора  на
число k» и «вектора
на
число k» и «вектора  на
число k».
на
число k».

Стоит также напомнить, что эти свойства позволяют выполнять преобразования в выражениях, содержащих суммы, разности векторов и произведения векторов на числа, так же как и в числовых выражениях.
Упростим следующие выражения.

Выполним задание, где рассмотрим куб ABCDA1B1C1D1, диагонали которого пересекаются в точке О. Для каждого из равенств нужно найти такое число k, чтобы равенства были верными.
Рассмотрим
первое равенство,  .
.
Для наглядности, изобразим каждый из данных векторов.

Рассмотрим грань ABCD, которая является квадратом, так как перед нами куб.
Это значит, что стороны AB и CD параллельны и равны.

Рассмотрим
следующее равенство  .
Изобразим векторы
.
Изобразим векторы  и
и
 .
.
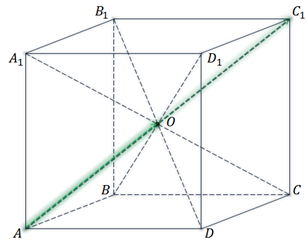
Понятно, что диагонали куба точкой пересечения делятся пополам.

Рассмотрим последнее
равенство  .
.
Изобразим
векторы  и
и
 .
.


Так мы с вами нашли значение числа k для каждого из равенств.
Выполним ещё одно задание.
Задача.
 параллелограмм.
Точки
параллелограмм.
Точки  и
и
 середины
сторон
середины
сторон  и
и
 соответственно.
соответственно.
 произвольная
точка пространства. Выразить:
произвольная
точка пространства. Выразить:
а)
 через
через
 б)
б)  через
через

Решение.
Обратимся к пункту А.


Обратим своё внимание на пункт Б.


Подведём итоги нашего урока.
Сегодня мы сформулировали определение произведения вектора на число в пространстве, которое ничем не отличается от аналогичного определения для векторов на плоскости.
Произведением
ненулевого вектора  на
число k называется такой
вектор
на
число k называется такой
вектор  ,
длина которого равна произведению модуля числа k
и длины данного вектора
,
длина которого равна произведению модуля числа k
и длины данного вектора  .
Причем векторы
.
Причем векторы  и
и
 сонаправлены,
если k≥0, и
противоположно направлены, если k<0.
сонаправлены,
если k≥0, и
противоположно направлены, если k<0.
Мы вспомнили свойства умножения вектора на число, известные нам из планиметрии, которые имеют место и для векторов в пространстве.
А также отметили, что, как и на плоскости, в пространстве любой ненулевой вектор пространства можно представить в виде произведения коллинеарного ему вектора на некоторое число k.
Все эти знания мы применили при выполнении заданий уже не на плоскости, а в пределах пространства.

 Получите свидетельство
Получите свидетельство Вход
Вход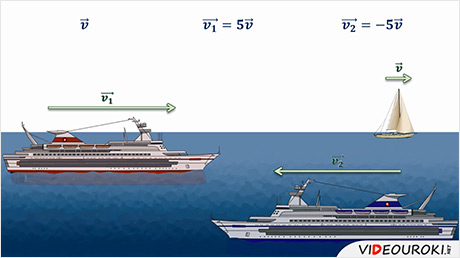



 0
0 6871
6871

