Материал урока.
Ранее мы ввели понятие вектора в пространстве, понятие равных векторов, правила сложения и вычитания векторов, а также произведение вектора на число.

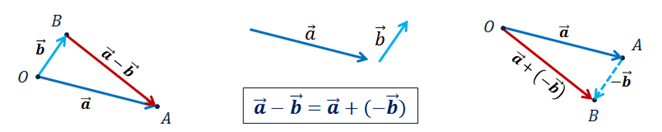

И все теоретические аспекты векторов в пространства практически совпадают с теорией векторов на плоскости. За исключением правила многоугольника сложения нескольких векторов. Многоугольник сложения в пространстве может быть и пространственным, то есть не все его вершины лежат в одной плоскости.
Сегодня мы с вами познакомимся с существенным и одним из главных отличий векторов на плоскости и векторов в пространстве. Мы введём понятие компланарных векторов.
Определение. Векторы называются компланарными, если при откладывании их от одной и той же точки они будут лежать в одной плоскости.
Но в связи с тем, что от любой точки пространства можно отложить вектор равный данному, и притом только один, можно это определение переформулировать так.
Векторы называются компланарными, если имеются равные им векторы, лежащие в одной плоскости.
Понятно, что любые два вектора всегда будут компланарными, ведь через них можно провести прямые, а через две прямые всегда можно провести единственную плоскость.
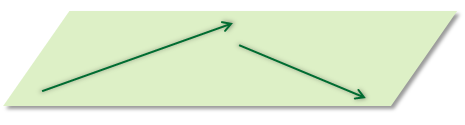
Если же рассмотреть три вектора, то они могут быть как компланарными, так и некомпланарными.
Компланарными они будут в том случае, когда среди них есть пара коллинеарных векторов.
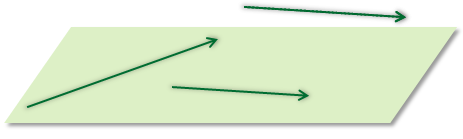
Тогда через один из коллинеарных векторов и вектор не коллинеарный ему можно провести плоскость. А для второго из коллинеарных векторов легко изобразить равный в этой плоскости.
Так мы получаем, что два вектора всегда будут компланарными, а три вектора будут компланарными, если среди них есть пара коллинеарных векторов.
Задача.
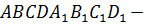 прямоугольный
параллелепипед.
прямоугольный
параллелепипед.
Компланарны ли векторы?
а)
 ,
,
 ,
,
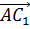
б)
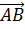 ,
,
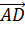 ,
,
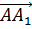
Решение.
Первой
рассмотрим тройку 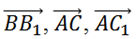 .
.
Через
векторы  и
и
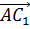 проведём
плоскость ACC1.
проведём
плоскость ACC1.
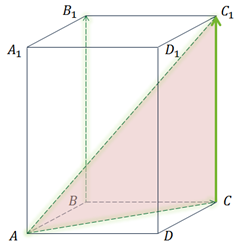
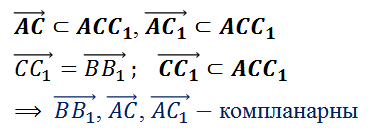
Рассмотрим
следующую тройку векторов. 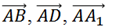 .
.

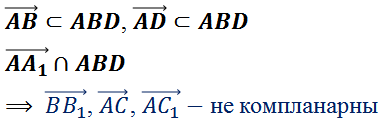
В этом задании мы, пользуясь определением, выяснили компланарны данные тройки векторов или нет.
Помимо определения компланарных векторов есть ещё и признак компланарности трёх векторов.
Если
вектор 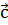 можно
разложить по векторам
можно
разложить по векторам  и
и
 ,
то есть представить его в таком виде
,
то есть представить его в таком виде  ,
где x и y
некоторые числа. То векторы
,
где x и y
некоторые числа. То векторы  ,
,
 и
и
 компланарны.
компланарны.
Докажем данный признак.
Рассмотрим
два неколлинеарных вектора  и
и
 ,
отложим их от некоторой точки О. Далее проведём через них плоскость.
,
отложим их от некоторой точки О. Далее проведём через них плоскость.
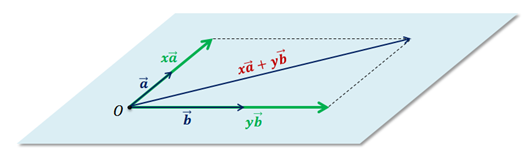
Очевидно,
что в этой же плоскости лежат векторы x и
y
и
y .
.
По
правилу параллелограмма построим вектор суммы векторов x и
y
и
y .
Полученный вектор суммы равен вектору
.
Полученный вектор суммы равен вектору  .
А по рисунку становится понятно, что векторы
.
А по рисунку становится понятно, что векторы  ,
,
 и
и
 действительно
лежат в одной плоскости, а значит, они компланарны.
действительно
лежат в одной плоскости, а значит, они компланарны.
Так мы доказали признак компланарности трёх векторов. Но справедливо и обратное утверждение, которое можно считать свойством трёх компланарных векторов.
Если
векторы  ,
,
 и
и
 компланарны,
а векторы
компланарны,
а векторы  ,
,
 не
коллинеарны, то вектор
не
коллинеарны, то вектор  можно
разложить по векторам
можно
разложить по векторам  и
и
 ,
причём коэффициенты разложения определяются единственным образом.
,
причём коэффициенты разложения определяются единственным образом.
Доказательство.
Итак,
воспользуемся тем, векторы компланарны, то есть лежат в одной плоскости. А из
курса планиметрии известно, что любой вектор плоскости можно разложить по двум
неколлинеарным векторам. Как раз векторы  и
и
 являются
такими по условию.
являются
такими по условию.
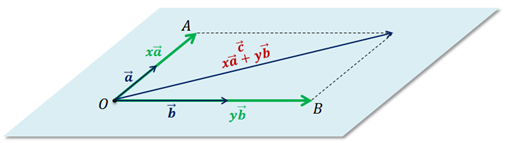
Тогда
отложим векторы  ,
,
 и
и
 от
некоторой точки О плоскости.
от
некоторой точки О плоскости.
Вектор
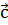 равен
сумме векторов
равен
сумме векторов 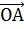 и
и
 ,
каждый из которых коллинеарен векторам
,
каждый из которых коллинеарен векторам  и
и
 соответственно.
Опираясь на коллинеарность, можем вектор
соответственно.
Опираясь на коллинеарность, можем вектор 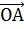 представить
в виде произведения вектора
представить
в виде произведения вектора  и
некоторого числа x, а вектор
и
некоторого числа x, а вектор  —
в виде произведения вектора
—
в виде произведения вектора  и
некоторого числа y.
и
некоторого числа y.
Отсюда
получаем, что вектор  равен
сумме произведений вектора
равен
сумме произведений вектора  на
число x
и
вектора
на
число x
и
вектора  на
число y.
на
число y.
Тем
самым мы смогли разложить вектор  по
векторам
по
векторам  и
и
 .
.
Что и требовалось доказать.
Задача.
Для параллелепипеда ABCDA1B1C1D1 среди данных троек векторов найти компланарные.
Решение.
Первой
рассмотрим тройку векторов 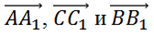 .
.

Все эти векторы коллинеарны, так как являются противоположными рёбрами параллелепипеда. А для компланарности трёх векторов достаточно коллинеарности хотя бы двух из них (в начале урока мы рассматривали такой случай). Поэтому можно утверждать, что данные векторы компланарны.
Далее
рассмотрим векторы 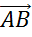 ,
, 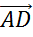 и
и 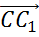 .
.
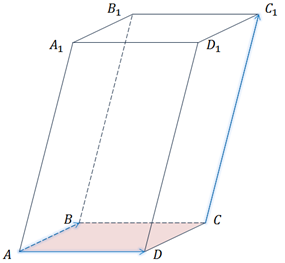
Векторы
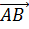 и
и
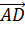 лежат
в одной плоскости, а вектор
лежат
в одной плоскости, а вектор 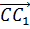 пересекает
её. Поэтому можно сказать, что данные векторы не компланарны.
пересекает
её. Поэтому можно сказать, что данные векторы не компланарны.
Следующей
рассмотрим тройку векторов  ,
,
 и
и
 .
.

Среди
них есть пара коллинеарных векторов,  и
и
 .
А значит, векторы данной тройки будут компланарны.
.
А значит, векторы данной тройки будут компланарны.
Осталось
рассмотреть тройку векторов 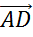 ,
, 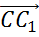 и
и 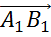 .
.
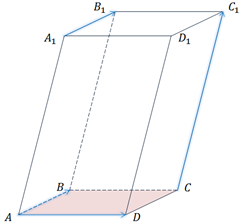
В
плоскости ABCD лежит вектор 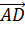 .
И вектор
.
И вектор 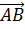 ,
равен вектору
,
равен вектору 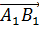 .
Но для вектора
.
Но для вектора 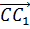 в
этой плоскости не найдётся равный, так как он пересекает её. Значит, векторы
данной тройки не будут являться компланарными.
в
этой плоскости не найдётся равный, так как он пересекает её. Значит, векторы
данной тройки не будут являться компланарными.
Так, пользуясь определением, мы нашли две тройки компланарных векторов.
Задача.
 тетраэдр. Точки
тетраэдр. Точки
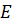 и
и
 —
середины сторон
—
середины сторон  и
и
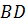 .
Доказать, что
.
Доказать, что 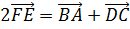 .
Компланарны ли векторы
.
Компланарны ли векторы 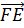 ,
,
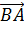 и
и
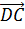 ?
?
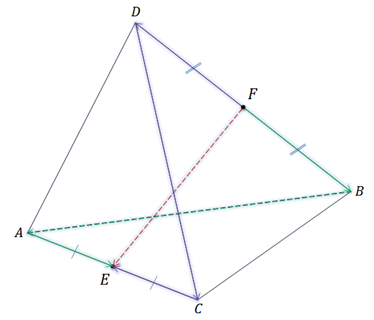
Итак, сначала проведём доказательство.
Пользуясь
правилом многоугольника сложения нескольких векторов в пространстве, можно
записать, что 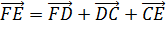 . С другой стороны вектор
. С другой стороны вектор 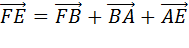 .
.
Сложим покомпонентно эти два равенства.
.
Векторы
 и
и
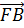 ,
а также
,
а также 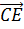 и
и
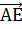 противоположны,
ведь их длины равны и они противоположно направлены. А значит, каждая из этих
сумм равна нулевому вектору.
противоположны,
ведь их длины равны и они противоположно направлены. А значит, каждая из этих
сумм равна нулевому вектору.
Тогда
мы получаем, что 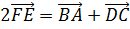 .
.
Что и требовалось доказать.
Теперь
ответим на вопрос, компланарны ли векторы 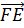 ,
,
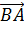 и
и
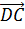 .
.
Разделим обе его части равенства, доказанного выше, на 2.
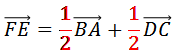
Так
мы записали разложение вектора 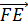 по
векторам
по
векторам 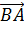 и
и
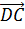 ,
где оба коэффициента разложения равны
,
где оба коэффициента разложения равны  .
.
Тогда по признаку компланарных векторов, данные векторы компланарны.
Подведём итоги нашего урока.
Сегодня мы ввели понятие компланарных векторов.
Векторы называются компланарными, если при откладывании их от одной и той же точки они будут лежать в одной плоскости.
На практике удобнее использовать такую формулировку: векторы называются компланарными, если имеются равные им векторы, лежащие в одной плоскости.
Так же мы выяснили, что любые два вектора всегда компланарны, а вот три вектора могут быть как компланарными, так и не компланарными.
В связи с этим мы доказали признак компланарности векторов.
Если
вектор  можно
разложить по неколлинеарным векторам
можно
разложить по неколлинеарным векторам  и
и
 ,
то векторы
,
то векторы  ,
,
 и
и
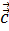 компланарны.
компланарны.
Справедливо также и обратное утверждение.
Если
векторы  ,
,
 и
и
 компланарны,
а векторы
компланарны,
а векторы  и
и
 не
коллинеарны, то вектор
не
коллинеарны, то вектор  можно
разложить по векторам
можно
разложить по векторам  и
и
 ,
причём коэффициенты разложения определяются единственным образом.
,
причём коэффициенты разложения определяются единственным образом.

 Получите свидетельство
Получите свидетельство Вход
Вход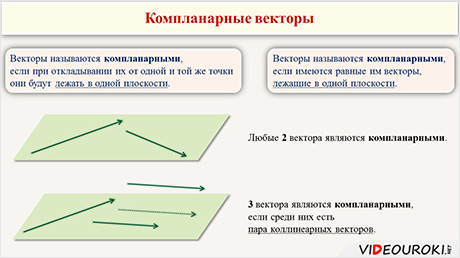



 0
0 19283
19283

