Материал урока.
На прошлых занятиях вы познакомились с понятием компланарных векторов.
Векторы называются компланарными, если при откладывании их от одной и той же точки они будут лежать в одной плоскости.
При этом на практике мы использовали такую формулировку: векторы называются компланарными, если имеются равные им векторы, лежащие в одной плоскости.
Так же вы доказали признак компланарности векторов.
Если
вектор 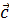 можно
разложить по векторам
можно
разложить по векторам 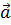 и
и
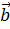 ,
то векторы
,
то векторы 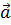 ,
,
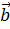 и
и
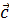 компланарны.
компланарны.
К тому же вы убедились в справедливости и обратного утверждения.
Если
векторы 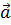 ,
,
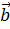 и
и
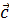 компланарны,
а векторы
компланарны,
а векторы 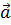 и
и
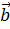 не
коллинеарны, то вектор
не
коллинеарны, то вектор 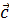 можно
разложить по векторам
можно
разложить по векторам 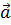 и
и
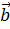 ,
причём коэффициенты разложения определяются единственным образом.
,
причём коэффициенты разложения определяются единственным образом.
Для сложения компланарных векторов, так как все они лежат в одной плоскости, можно использовать правила сложения известные из планиметрии, а именно: правило треугольника, правило параллелограмма и правило многоугольника.
Что же касается некомпланарных векторов, то для построения их суммы используют правило параллелепипеда.
Рассмотрим
некомпланарные векторы 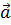 ,
,
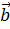 и
и
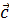 .
.
От
произвольной точки О пространства отложим векторы  ,
,
 и
и
 равные
векторам
равные
векторам 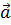 ,
,
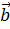 и
и
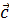 соответственно.
соответственно.
На полученных векторах можно построить параллелепипед так, чтобы они являлись его рёбрами.
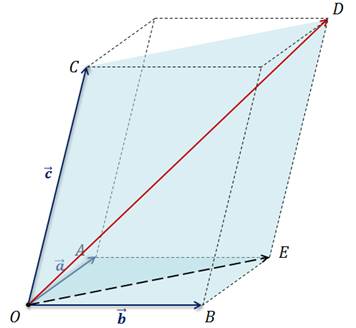
Построим
вектор суммы векторов  ,
,
 и
и
 при
этом последовательно их складывая.
при
этом последовательно их складывая.
Вектором
суммы векторов  ,
,
 по
правилу параллелограмма будет вектор
по
правилу параллелограмма будет вектор  .
.
Вектором
суммы векторов  и
и
 по
тому же правилу будет вектор
по
тому же правилу будет вектор  .
Вектор
.
Вектор  равен
сумме векторов
равен
сумме векторов  ,
,
 и
и
 ,
а значит равен сумме векторов
,
а значит равен сумме векторов 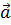 ,
,
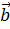 и
и
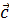 .
.
Отсюда правило параллелепипеда можно сформулировать так.
Если
отложить некомпланарные векторы 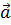 ,
,
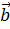 и
и
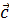 от
некоторой точки пространства О и построить на них параллелепипед, то диагональ OD
параллелепипеда будет выражать вектор суммы данных векторов.
от
некоторой точки пространства О и построить на них параллелепипед, то диагональ OD
параллелепипеда будет выражать вектор суммы данных векторов.
Воспользуемся сформулированным только что правилом и выполним задание.
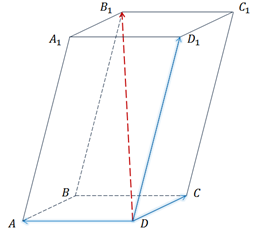
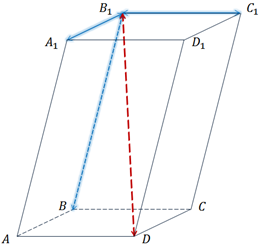
Рассмотрим
 параллелепипед
и укажем вектор суммы данных векторов такой, чтобы его начало и конец совпадали
с вершинами параллелепипеда.
параллелепипед
и укажем вектор суммы данных векторов такой, чтобы его начало и конец совпадали
с вершинами параллелепипеда.
Первым
назовём вектор  .
Так как эти векторы отложены от одной точки и являются рёбрами данного
параллелепипеда, то вектор их суммы будет задавать диагональ параллелепипеда,
одним из концов которой будет точка начала данных векторов А. Так мы получим
вектор
.
Так как эти векторы отложены от одной точки и являются рёбрами данного
параллелепипеда, то вектор их суммы будет задавать диагональ параллелепипеда,
одним из концов которой будет точка начала данных векторов А. Так мы получим
вектор  .
.

Далее
назовём вектор суммы векторов  .
.
Они
также отложены от одной точки D
и являются рёбрами данного параллелепипеда. Вектором их суммы будет вектор  .
.
В
следующем пункте нужно назвать вектор суммы векторов  .
.
В данном случае векторы не имеют общего начала, а имеют общий конец.
Выразим каждый из данных векторов через противоположный.



Далее
рассмотрим сумму векторов  .
Только вектор
.
Только вектор  не
берёт своё начало в точке А1. Но вектор
не
берёт своё начало в точке А1. Но вектор  равен
ему, поэтому заменим вектор
равен
ему, поэтому заменим вектор  в
сумме на равный ему вектор
в
сумме на равный ему вектор  .
.
Не
трудно понять, что вектором полученной суммы будет вектор  .
.
Последней
рассмотрим сумму векторов  .
.
Вектор
 заменим
равным ему вектором
заменим
равным ему вектором  .
Тогда не трудно записать вектор суммы. Им будет вектор
.
Тогда не трудно записать вектор суммы. Им будет вектор 

Подведём итоги урока.
Сегодня мы описали правило параллелепипеда сложения трёх некомпланарных векторов.
Если
отложить некомпланарные векторы 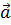 ,
,
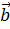 и
и
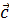 от
некоторой точки пространства О и построить на них параллелепипед, то диагональ OD
параллелепипеда будет выражать вектор суммы данных векторов.
от
некоторой точки пространства О и построить на них параллелепипед, то диагональ OD
параллелепипеда будет выражать вектор суммы данных векторов.
Это правило пригодится вам при изучении следующих тем курса стереометрии.

 Получите свидетельство
Получите свидетельство Вход
Вход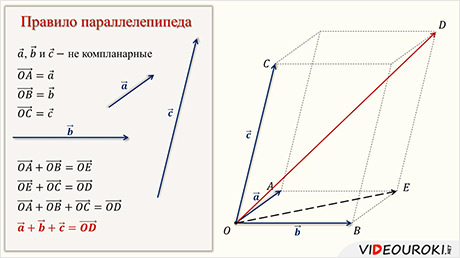



 0
0 20118
20118



