Саша и Паша гуляли во дворе и разговаривали.
– Саш, вот ты как думаешь, какое наземное животное самое большое на Земле?
– Я думаю, что слон.
– А какой слон? Они же бывают африканскими и азиатскими.
– Ой, я даже не знаю. Я думал, что только один вид слонов бывает.
– Пошли ко мне, у меня есть энциклопедия, в которой можно прочитать о том, сколько весят слоны.
– Пойдём.
– Так, давай посмотрим.
Здесь написано, что самец африканского слона весит 8,5 тонн, вес самки может доходить до 2,8 тонн. А вот вес самца азиатского слона может быть равен 5,2 тонны. Самка азиатского слона может весить 2,7 тонны.

– Так. Давай теперь выпишем вес самцов и самок и посмотрим, кто же весит больше.
– Ну с самцами всё просто. Самец африканского слона весит больше, чем самец азиатского слона. Потому что 8 целых намного больше 5 целых. А вот с самками непонятно.
Обе весят по 2 целых. Как же их сравнивать? Паша, ты как думаешь?

– Даже не знаю, Саша. С таким я ещё не сталкивался. Но я знаю, кто может нам помочь. Электроша.
– Он точно знает, как можно сравнить такие числа.
– Электроша, привет. Мы опять к тебе, и у нас новая задача.
– Здравствуйте, мальчики. Что случилось на этот раз?
Мы хотим узнать, какой слон – африканский или азиатский – весит больше. С самцами нам понятно, 8 > 5, поэтому африканский слон весит больше азиатского. А вот с самками – нет. Смотри, самка африканского слона весит 2,8 тонны, а самка азиатского слона весит 2,7 тонны. Если бы они весили 28 и 27 тонн, то сравнить их не составило бы труда. А как быть здесь?
Сейчас я вам всё расскажу, но сначала выполним несколько заданий устно.

Вернёмся к вашим числам.
Вес самцов вы сравнили абсолютно правильно. Сами того не зная, вы применили правило о том, что из двух десятичных дробей больше та, у которой целая часть больше.
А вот с весом самок надо поступить так. Поскольку целые части равны, то сравним десятые. Мы видим, что в разряде десятых у самки африканского слона стоит 8, а у азиатского – 7. 8 > 7, значит, и самка африканского слона весит больше чем самка азиатского слона.

– Вам понятно?
– Да, Электроша, мы поняли.
– Тогда выполните задание.
Сравните числа:  .
.
Саша, начинай.
–  . 7 < 17, значит,
первая дробь меньше второй.
. 7 < 17, значит,
первая дробь меньше второй.
 . Целые части равны, сравним числа, которые
стоят в разряде десятых. 7 < 9, значит, вторая
дробь больше первой.
. Целые части равны, сравним числа, которые
стоят в разряде десятых. 7 < 9, значит, вторая
дробь больше первой.
И последняя пара чисел  . Целые части у них равны. В разряде десятых стоят одинаковые цифры, в
разряде сотых тоже. А вот в разряде тысячных у первого числа стоит 9, а у
второго – 5. Значит, первое число больше второго.
. Целые части у них равны. В разряде десятых стоят одинаковые цифры, в
разряде сотых тоже. А вот в разряде тысячных у первого числа стоит 9, а у
второго – 5. Значит, первое число больше второго.
– Молодец, Саша.

Теперь давайте попробуем сравнить вот такие дроби:  и
и  . Смотрите, целые части этих дробей
одинаковые, но в дробной части находится разное количество цифр.
. Смотрите, целые части этих дробей
одинаковые, но в дробной части находится разное количество цифр.
Давайте попробуем сравнить отрезки, длины которых равны 17,5 метра и 17,50 метра. Переведём длины в сантиметры.
17,5 метра – это 17 метров и 5 дециметров, значит, длина первого отрезка равна 1750 сантиметрам.
Теперь переведём 17,50 метра в сантиметры. Получим 17 метров 50 сантиметров или 1750 сантиметров.
– Электроша, получается, отрезки равны? То есть 17,5 = 17,50?

– Да, мальчики. Вы правы. Сформулируем правило.
Если к десятичной дроби справа приписать любое количество нулей, то получится дробь, равная данной. Значение дроби, которая оканчивается нулями, не изменится, если последние нули в её записи отбросить.

Давайте попробуем сравнить такие дроби: 8,6 и 8,589.
Целые части этих чисел равны. Но количество цифр в дробной части разное.
Чтобы сравнить эти числа, допишем в первой дроби после шести десятых нули. Как вы думаете, сколько нулей нам надо дописать?
– Я думаю, что надо дописать 2 нуля, чтобы количество цифр в дробных частях было одинаковым.
– Да, Паша, ты абсолютно прав.
Получим дробь 8,600. И теперь мы можем сравнить эту дробь с дробью 8,589.
Сравнивая цифры, которые стоят в разряде десятых, получим, что первая дробь больше второй 8,600 > 8,589.

И запомним правило.
Чтобы сравнить две десятичные дроби с равными целыми частями и различным количеством цифр после запятой, надо с помощью приписывания нулей справа уравнять количество цифр в дробных частях, после чего сравнить полученные дроби поразрядно.

– Ребята, вам всё ясно?
– Да.
– Тогда выполните простое задание.
Уравняйте количество цифр в дробях:  .
.
Паша, приступай к решению.
– Самое большое количество цифр в доброй части – это 4. Значит, к первой дроби надо приписать 2 нуля, ко второй – 1, а к четвёртой – 1 ноль.

– Молодец! Вот ещё одно задание для вас.
Сравните числа:  .
.
Саша, это задание для тебя.
– В первой паре дробей больше первая дробь, потому что у неё целая часть больше, чем целая часть второй дроби.
Сравним дроби  . Целые части равны, цифры, которые стоят в разряде десятых, равны. А вот
в разряде сотых у первой дроби стоит 3, а у второй – 4, значит, первая дробь
меньше второй.
. Целые части равны, цифры, которые стоят в разряде десятых, равны. А вот
в разряде сотых у первой дроби стоит 3, а у второй – 4, значит, первая дробь
меньше второй.
Третья пара чисел  . У первой дроби в дробной части всего одна цифра, а у второй – две.
Допишем к первой дроби справа ноль. Целые части чисел равны. В разряде десятых
у первой дроби – 6, а у второй – 8. Значит, вторая дробь больше первой.
. У первой дроби в дробной части всего одна цифра, а у второй – две.
Допишем к первой дроби справа ноль. Целые части чисел равны. В разряде десятых
у первой дроби – 6, а у второй – 8. Значит, вторая дробь больше первой.
– Молодец.

Вот для вас ещё одно задание.
Какие цифры можно вставить вместо звёздочек,
чтобы получились верные неравенства:  .
.
Паша, это задание для тебя.
– Целые части дробей равны. У второй дроби в разряде десятых стоит 5. В разряде сотых у обеих дробей стоит одинаковое число. Значит, для того, чтобы первая дробь была меньше второй, в разряд десятых можно поставить цифры 0, 1, 2, 3 или 4.
Перейдём ко второму неравенству.
Целые части одинаковые, в разряде десятых тоже стоят одинаковые цифры. В разряде сотых у меньшей дроби стоит 7. Значит, вместо звёздочки можно поставить 8 или 9.
– Молодец.

Вот для вас ещё одно задание.
Запишите дроби в порядке возрастания:  .
.
Это задание для тебя, Саша.
– Так, в порядке возрастания – это значит от меньшего к большему.
Поскольку у дробей разное количество цифр после запятой, допишем к первой дроби и к третьей – по одному нулю.
Целые части дробей одинаковы, сравним цифры в разряде десятых. Мы видим, что самая маленькая цифра у этой дроби, значит её запишем первой. У остальных дробей цифры, которые стоят в разряде десятых, равны. Сравним цифры в разряде сотых.
Тогда на втором месте надо записать вот эту дробь. На третьем – эту, и самая большая дробь – 15,86.
– Молодец, Саша.

Вот вам последнее задание на сегодня.
Расположите дроби в порядке убывания:  .
.
Паша, попробуй ты.
– Понятно, что самой большой будет дробь 7,97. Потому что у неё целая часть больше, чем у остальных дробей.
Среди оставшихся самая большая дробь 3,53. У неё в разряде десятых стоит самая большая цифра из оставшихся дробей. Третьей запишем дробь 3,47. И самая маленькая дробь – 3,43.

– Молодцы, мальчики. Вы всё правильно решили.

 Получите свидетельство
Получите свидетельство Вход
Вход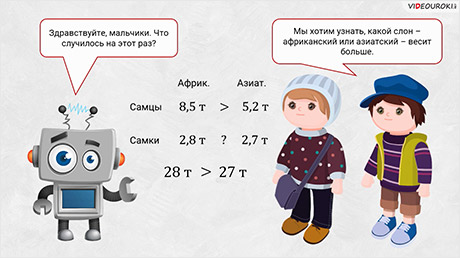



 0
0 3600
3600

