Саша и Паша гуляли во дворе и разговаривали. И тут Паша сказал:
– Представляешь, мы вчера на даче, просто ради смеха, решили измерить площадь участков. Наш и тёти Тани.
И оказалось, что площадь нашего участка – 6,17 сотки, а у тёти Тани площадь участка – 6,43 сотки. Хотя мы всегда всем говорим, что площадь нашего участка 6 соток.
Выходит, что мы всех обманываем? И надо говорить, что у нас на даче участок, площадь которого 6,17 сотки?
– Не знаю, Паша. Мы тоже говорим, что площадь нашего участка 9 соток, хотя никогда его не измеряли. Может, и у нас площадь не равна 9 соткам.
И вообще, когда люди рассказывают про свои дачи, они называют целое число соток. Я ещё всегда удивлялся, как можно так точно измерить землю? Там же ямы, бугорки точно измерить нельзя.

– Пойдём к Электроше, может, он нам разъяснит – обманываем мы всех или нет?
– Электроша, здравствуй. Мы снова к тебе и снова с вопросом.
– Здравствуйте, мальчики. Задавайте свой вопрос.
– Вот смотри, площадь нашего дачного участка – 6,17 соток, а мы всем говорим, что у нас участок площадью 6 соток. Получается, что мы всех обманываем?
– Успокойся, Паша, никого вы не обманываете. Сейчас я вам всё расскажу. Но сначала давайте немного устно порешаем.

Итак, вернёмся к вашему вопросу.
– Нет, Паша, вы никого не обманывали. В данном случае 6 соток – это приближённое значение числа 6,17. В таких случаях говорят, что число округлили до числа 6.
Записывают это так  .
.

– Подожди, Электроша, а что это за знак? Какое-то неправильное равно?
Я понял, это Электроша решил просто красивое волнистое равно поставить. Так, Электроша?
– Нет, мальчики. Это специальный знак, который используется при округлении числа. Читается он так: «приблизительно равно».
А всю запись читают так: «шесть целых семнадцать сотых приближённо равно шести».
– Ага, понятно.
То есть мы просто взяли и отбросили дробную часть? Тогда если я захочу округлить, ну, например, 17,95, то я напишу просто 17?
– Нет, Паша. Не совсем так. Это число округляется до 18.
Подожди, а 18 здесь причём? Мы же округляем 17,95.
Давайте на координатном луче отметим точку 17,95. К какому числу ближе 17,95?
– К 18.
– Правильно. Именно поэтому число и округлили до 18.
Договорились округлять к числу, которое находится ближе.
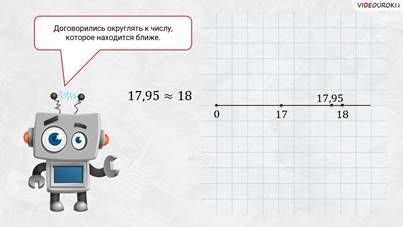
Давайте попробуем выполнить задание.
На координатном луче изображены точки с координатами: А (8,1); В (8,3); С (8,7); D (8,9). Округлите координаты этих точек.
Начинай ты, Саша.
8,1 ближе к 8. Значит, округлим это число до 8.
8,3 тоже ближе к 8.
А вот 8,7 десятых ближе к 9, значит, и округлять это число мы будем до 9.
8,9 мы тоже округлим до 9.

– Молодцы, ребята, а как вы думаете, число 8,5 до какого числа надо округлять?
– Не знаем, оно же находится на одинаковом расстоянии и от 8, и от 9.
– В таком случае всегда число округляют в большую сторону, то есть 8,5 мы должны округлить до 9.

До этого момента мы с вами округляли все дроби до целых частей. Но на самом деле округлять можно до любого разряда.
Вот, например, попробуем округлить число 0,12 до десятых.
Изобразим координатный луч и поставим на нём точку А с координатой 0,12. Поскольку нам надо округлить до десятых, то посмотрим, к какому числу эта дробь ближе: к 0,1 или 0,2? Как ты думаешь, Паша?
– К 0,1.
– Да, Паша, ты прав. Значит, и округляем мы 0,12 до 0,1.

Но каждый раз изображать координатный луч не очень удобно. Существует правило, которое помогает округлять любые числа до любых разрядов.
Сформулируем его.
Для того, чтобы десятичную дробь округлить до единиц, десятых, сотых и так далее, надо все следующие за этим разрядом цифры отбросить.
Если при этом первая из цифр, которые мы отбрасываем, равна 0, 1, 2, 3 или 4, то последняя из оставшихся цифр не меняется.
Если же первая из отбрасываемых цифр равна 5, 6, 7, 8 или 9, то последняя из оставшихся цифр увеличивается на единицу.

– Что-то не очень понятно. Электроша, ты можешь объяснить это правило ещё раз?
– Конечно. Смотрите, пусть нам нужно округлить число 7,359 до разряда десятых. Мы должны отбросить 59. Первая отбрасываемая цифра – 5, значит цифру в разряде десятков увеличиваем на единицу. Получаем, что число 7,359 до разряда десятых округляется до числа 7,4.
А вот для округления числа 5,128 до разряда десятых надо просто отбросить последние две цифры. Потому что первая из отброшенных цифр равна 2.

– Вам стало понятно?
– Да, Электроша. Можешь нам дать задание и проверить, как мы всё поняли.
– Хорошо, выполните округление чисел: а) до десятых:  б) до сотых:
б) до сотых: 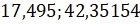 .
.
Это задание для тебя, Паша.
Итак, первая дробь 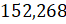 . Откидываем последние две цифры. Первая цифра, которую мы откинули,
равна 6, значит цифру в разряде десятых увеличим на единицу.
. Откидываем последние две цифры. Первая цифра, которую мы откинули,
равна 6, значит цифру в разряде десятых увеличим на единицу.
У второй дроби 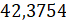 отбросим последние три цифры. Первая из отбрасываемых
– 7, значит 3 увеличиваем до 4.
отбросим последние три цифры. Первая из отбрасываемых
– 7, значит 3 увеличиваем до 4.
– Молодец, Паша. Теперь очередь Саши порешать.
У первой дроби 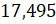 надо отбросить одну цифру. Эта цифра равна 5,
значит, получим 17,50. Подожди, Электроша, но это же
равно 17,5?
надо отбросить одну цифру. Эта цифра равна 5,
значит, получим 17,50. Подожди, Электроша, но это же
равно 17,5?
– Нет, Саша. Когда речь идёт об округлении, последние нули в записи десятичной дроби не отбрасываются. Они показывают разряд, до которого мы округляли.
– Понятно. Округлим последнюю дробь 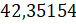 . Отбросим последние три цифры. Первая отбрасываемая цифра равна 1,
значит, увеличивать цифру 5 не надо.
. Отбросим последние три цифры. Первая отбрасываемая цифра равна 1,
значит, увеличивать цифру 5 не надо.
– Молодцы, ребята. Вы хорошо справились.

Но округлять можно не только десятичные дроби, но и натуральные числа.
Так поступают очень часто. Например, знаете ли вы, сколько жителей в городе Москве?
Приблизительно 12 400 000 человек. Обратите внимание, мы сказали приблизительно. Потому что если мы заглянем, например, в интернет-энциклопедию Википедия, то увидим, что на 2017 год население города Москвы составляет 12 380 664 человека.

Округление натуральных чисел очень похоже на округление десятичных дробей.
При округлении натуральных чисел до какого-либо разряда вместо всех следующих за ним цифр младших разрядов пишут нули. При этом, если первая из цифр, следовавших за этим разрядом, была равной 5, 6, 7, 8 или 9, то цифра в данном разряде увеличивается на единицу.

Пробуем округлить до разряда десятков число 185 757. Записываем 0 вместо 7, а 5 увеличиваем на 1 и получаем число 185 760.

Попробуйте выполнить упражнение.
– Округлите до десятков, сотен и тысяч число 5372.
Паша, это задание для тебя.
Заменим последнюю цифру нулём. Эта цифра равна 2, значит, это число округляем до 5370.
Теперь две последние цифры заменим нулями. Поскольку в разряде десятков стоит число 7, округляем до 5400.
И, округляя число до тысяч, получим 5000.
– Молодец, Паша.

Теперь давайте разберём такую задачу.
До места назначения водителю осталось проехать всего 279 километров. Расход бензина составляет 9 литров на 100 километров. Объём топливного бака равен 60 литрам. Стрелка на спидометре стоит в таком положении. Водитель спокоен – ему точно хватит бензина до конца маршрута. Как водителю удалось быстро произвести расчёты?
– Мальчики, у вас есть какие-то предположения?
– Нет.
– Всё очень просто. Водитель округлил расход топлива на 100 километров до 10 литров. Оставшееся расстояние округлил до 300 километров. Выполнив простое действие, водитель рассчитал, что на оставшийся путь ему нужно 30 литров бензина. Это половина бака, а мы видим, что в баке бензина больше, чем половина.
Конечно, более точный ответ водитель мог получить, если бы 279 разделил на 100 и умножил на 10. Но это сложное вычисление, и оно решается дольше, чем то, которое решали мы. Водитель просто прикинул значение числового выражения.
Обратите внимание, что водитель округлял все числа в большую сторону: и количество километров, и расход топлива. Если топлива хватит при таких округлённых данных, то на самом деле его точно будет достаточно.

Прикидку нужно применять тогда, когда можно заменить трудные вычисления простыми расчётами.
Например, вы приглашаете гостей и хотите приготовить праздничный стол. Идя в магазин, вы сначала прикидываете, сколько что будет стоить и, исходя из этой прикидки, берёте с собой деньги.
– Вам всё понятно, ребята?
– Да.
– Тогда выполните последнее задание.
Саша, представь, что у тебя есть 500 рублей. Ты хочешь купить Паше на день рождения 24 шоколадки по 18 рублей каждая. Используя прикидку, определи, хватит ли тебе денег?
– Так, округлим стоимость шоколадок до 20 рублей, а их количество – до 25.
Умножим 20 на 25 и получим 500 рублей. Я округлял в большую сторону, значит, и на самом деле мне хватит этих денег на 24 шоколадки.

– Молодец.

 Получите свидетельство
Получите свидетельство Вход
Вход



 0
0 8617
8617


