Числовые последовательности (определение, примеры, свойства)

Вопросы занятия:

·     познакомиться с понятием числовой последовательности;

·     рассмотреть способы задания числовых последовательностей.

Материал урока.

Мы с вами приступаем к изучению темы «Производная» и начнём с повторения понятия числовой последовательности. С этим понятием вы знакомились в курсе алгебры базовой школы.

Давайте вспомним, что же такое числовая последовательность, и какими свойствами она обладает.

Определение.

Функцию вида y = f(x), где x принадлежит множеству натуральных чисел называют функцией натурального аргумента или числовой последовательностью и обозначают

y = f (n)

y₁, y₂, y₃,…,y_n,…

(y_n).

Давайте теперь вспомним способы задания последовательностей.

Последовательность задана аналитически, если указана формула её n -ого члена, y_n = f(n).

Например:

При словесном способе задания последовательности: последовательность, каждый её член, возможность вычисления каждого её члена можно задать словами, не обязательно формулами.

При рекуррентном задании последовательности задаются правила вычисления энного члена по предыдущим членам.

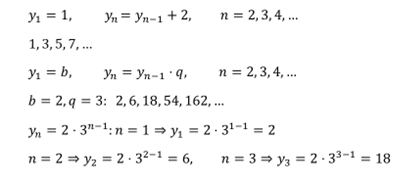
Давайте вспомним свойства числовых последовательностей.

Последовательность (y_n) называется ограниченной сверху, если все её члены не больше некоторого числа. Другими словами, последовательность (y_n) ограничена сверху, если существует число M такое, что для любого n выполняется неравенство: y_n ≤ M.

Число M называется верхней границей последовательности.

Например,

Последовательность (y_n) называется ограниченной снизу, если все её члены не больше некоторого числа. Другими словами, последовательность (y_n) ограничена снизу, если существует число m такое, что для любого n выполняется неравенство: y_n ≥ m.

Число m называется нижней границей последовательности.

Например,

Если последовательность ограничена и сверху и снизу, то её называют ограниченной последовательностью.

Рассмотрим пример.

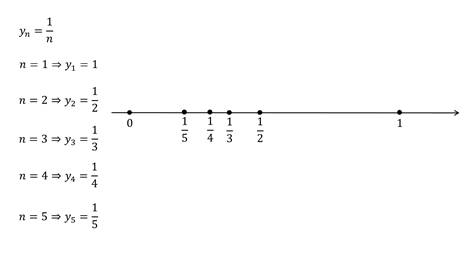
Таким образом, ограниченность последовательности означает, что все члены последовательности (точнее, соответствующие им точки прямой) принадлежат некоторому отрезку.

Последовательность (y_n) называется возрастающей, если каждый последующий член больше предыдущего, то есть верно неравенство

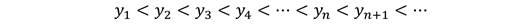
Например,

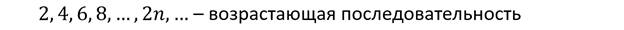
Последовательность (y_n) называется убывающей, если каждый её член меньше предыдущего, то есть верно неравенство

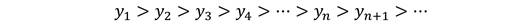
Например,

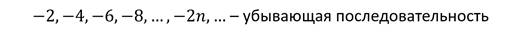
Возрастающие и убывающие последовательности объединяют общим термином – монотонные последовательности.

Рассмотрим несколько примеров.

Пример.

Пример.