Преобразование произведения в сумму

Вопросы занятия:

·     познакомиться с формулами преобразования произведений тригонометрических функций в сумму;

·     рассмотреть примеры использования этих формул для решения задач.

Материал урока.

Прежде чем приступить к изучению нового материала, давайте выполним упражнение.

Упражнение.

Давайте упростим выражение sin (s + t) + sin (s – t).

Давайте упростим выражение cos (s + t) + cos (s – t).

Давайте упростим выражение cos (s + t) - cos (s – t).

Рассмотрим пример.

Пример.

Рассмотрим ещё один пример.

Пример.

Рассмотрим ещё один пример.

Пример.

Мы с вами завершаем изучение темы «Тригонометрические преобразования». Давайте соберём все формулы тригонометрии и расположим их так, чтобы ими удобно было пользоваться. Не забываем, что эти формулы применяются только при допустимых значениях аргументов.

Итак, начнём с категории формул, связывающих тригонометрические функции одного и того же аргумента.

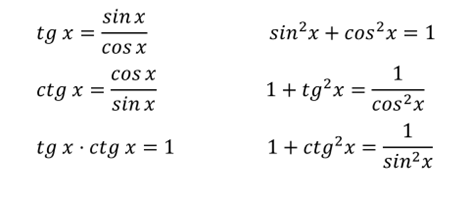
Формулы, связывающие функции аргументов, из которых один вдвое больше другого.

Формулы сложения аргументов.

Преобразование сумм тригонометрических функций в произведение.

Преобразование произведений тригонометрических функций в суммы.

Формулы приведения.