Вопросы занятия:
· познакомиться с понятием сходимости последовательностей;
· познакомиться с понятием предела числовой последовательности.
Материал урока.
Прежде чем приступить к изучению нового материала, давайте выполним упражнение.
Упражнение.

Рассмотрим две числовые последовательности (xn) и (yn).
Изобразим члены этой последовательности точками на числовых прямых.

Легко заметить, что члены последовательности (xn) как бы сгущаются к точке ноль, а у последовательности (yn) такой точки сгущения нет. В таких случаях говорят, что последовательность (xn) сходится, а последовательность (yn) – расходится.
В математике термин точка сгущения заменяется термином предел последовательности.
Давайте дадим определение пределу последовательности.
Определение.
Число b называют пределом последовательности (yn), если в любой заранее выбранной окрестности точки b содержаться все члены последовательности, начиная с некоторого номера.
В таком случае пишут

В определении появился новый термин – окрестность. Давайте разбер`мся, что это такое. Интервал (a – r; a + r) будем называть окрестностью точки а, а число r – радиусом окрестности.

То есть наше определение можно понимать так:

Понятие предела использовалось ещё Ньютоном во второй половине семнадцатого века и математиками восемнадцатого века такими как Эйлер и Лагранж, однако они понимали предел интуитивно.
Первые строгие определения предела последовательности дали Больцано в 1816 году и Коши в 1821 году.
Для рассмотренной выше последовательности (xn) = 1/n можно записать соотношение:

Легко заметить, что и для последовательности (yn) предел равен нулю.

Обобщая предыдущие две последовательности, можно записать:
![]()
Рассмотрим последовательности.

Подставляя вместо q другие числа, по модулю больше единицы, можно заметить, что справедливо утверждение:
![]()
Рассмотрим свойства сходящихся последовательностей.

В девятнадцатом веке немецкий математик Карл Вейерштрасс доказал, что если последовательность не только ограничена, но и монотонна (убывает или возрастает), то она обязательно сходится. То есть можно записать третье свойство сходящихся последовательностей.

Сегодня на уроке мы вывели:

Добавим ещё одно соотношение:
![]()
Другими словами, предел стационарной последовательности равен значению любого члена последовательности.
Указанные выше соотношения используются для вычисления пределов в более сложных случаях. Для этого же используется и следующая теорема.

Рассмотрим несколько примеров.
Пример.

Пример.

Из этих примеров видно, что для любого натурального показателя m и любого коэффициента k справедливо соотношение:

Рассмотрим ещё несколько примеров.
Пример.

Пример.


 Получите свидетельство
Получите свидетельство Вход
Вход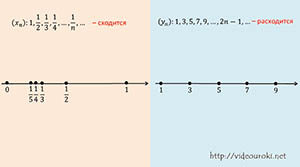



 0
0 8954
8954

